标签:编号 turn 简单选择排序 操作方法 数组元素 inf color class 置换
三 ,选择排序
从算法逻辑上看,选择排序是一种简单直观的排序算法,在简单选择排序过程中,所需移动记录的次数比较少。
1,基本思想
选择排序的基本思想:比较+交换
在待排序的一组数据中,选出最小(最大)的一个数与第一个位置的数交换,然后在剩下的数中,再找最小(最大)的数与第二个位置的数交换位置,
依次类推,直到第N-1个元素与第N个元素交换位置,选择排序结束。
2,过程描述
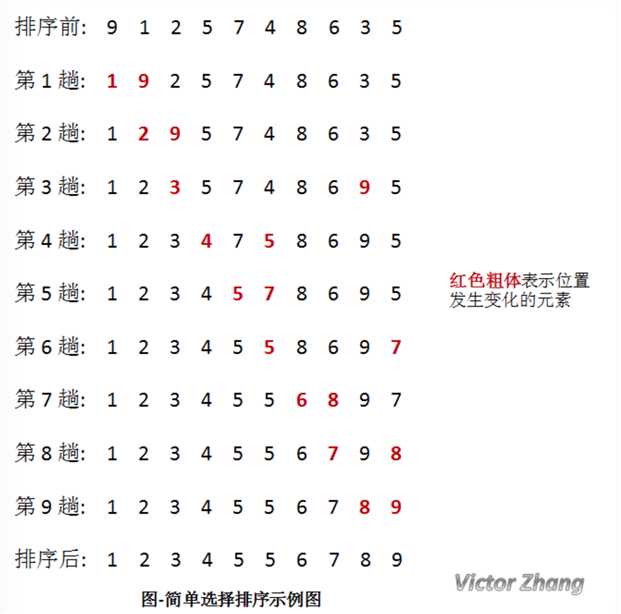
操作方法:
第一趟:从n个记录中找出关键码最小的记录和第一个记录交换;
第二趟:从第二个记录开始的n-1个记录中再选出关键码最小的记录与第二个记录交换
以此类推......
第i趟,则从第i个记录开始的n-i+1个记录中选出关键码最小的记录与第i个记录交换,直到整个序列按关键码有序。
3,代码案例:
public class SelectSort { public static void main(String[] args) { //定义一个数组 int arr[]={3,1,2,5,4}; SelectSort(arr); System.out.println("选择排序:"+Arrays.toString(arr)); } public static void SelectSort(int[] array) { //判断数组为空或为一个元素的情况 if (null == array || array.length <= 1) { return; } //数组比较次数n-1 for (int i = 0; i < array.length - 1; i++) { int min = i;//保存当前最小元素的位置 //遍历待排序数组元素(i之后的元素) for (int j = i + 1; j < array.length; j++) { //如果已排序中 较大元素 大于 待排序元素中的 最小元素 则更换元素对应索引 if (array[min] > array[j]) { min = j; } //确保找出待排序的最小元素的编号 } //置换位置 int temp = array[min]; array[min] = array[i]; array[i] = temp; } } }
4,选择排序的时间复杂度
简单选择排序的比较次数与序列的初始排序无关。假设待排序的系列有N个元素,则比较次数总是N(N-1)/2
而移动次数与系列的初始排序有关,当排序正序时,移动次数最少,为0
当序列反序时,移动次数最多,为3N(N-1)/2
所以,综上,简单排序的时间复杂度为O(N*N)
| 平均时间复杂度 | 最好情况 | 最坏情况 | 空间复杂度 |
|---|---|---|---|
| O(n²) | O(n²) | O(n²) | O(1) |
选择排序的简单和直观名副其实,这也造就了它”出了名的慢性子”,无论是哪种情况,哪怕原数组已排序完成,它也将花费将近n²/2次遍历来确认一遍。
即便是这样,它的排序结果也还是不稳定的。 唯一值得高兴的是,它并不耗费额外的内存空间。
法,在简单选择排序过程中,所需移动记录的次数比较少。
标签:编号 turn 简单选择排序 操作方法 数组元素 inf color class 置换
原文地址:https://www.cnblogs.com/2019wxw/p/11234072.html