标签:默认 最长回文子串 lan size 大于 开始 www 半径 man
Manacher Algorithm算法,俗称马拉车算法,其时间复杂为O(n)。该算法是利用回文串的特性来避免重复计算的,至于如何利用,且由后面慢慢道来。
在时间复杂度为O(n^2)的算法中,我们在遍历的过程要考虑到回文串长度的奇偶性,比如说“abba”的长度为偶数,“abcba”的长度为奇数,这样在寻找最长回文子串的过程要分别考奇偶的情况,是否可以统一处理了?
一)第一步是改造字符串S,变为T,其改造的方法如下:
在字符串S的字符之间和S的首尾都插入一个“#”,如:S=“abba”变为T="#a#b#b#a#" 。我们会发现S的长度是4,而T的长度为9,长度变为奇数了!!那S的长度为奇数的情况时,变化后的长度还是奇数吗?我们举个例子,S=“abcba”,变化为T=“#a#b#c#b#a#”,T的长度为11,所以我们发现其改造的目的是将字符串的长度变为奇数,这样就可以统一的处理奇偶的情况了。
二)第二步,为了改进回文相互重叠的情况,我们将改造完后的T[ i ] 处的回文半径存储到数组P[ ]中,P[ i ]为新字符串T的T[ i ]处的回文半径,表示以字符T[i]为中心的最长回文字串的最端右字符到T[i]的长度,如以T[ i ]为中心的最长回文子串的为T[ l, r ],那么P[ i ]=r-i+1。这样最后遍历数组P[ ],取其中最大值即可。若P[ i ]=1表示该回文串就是T[ i ]本身。举一个简单的例子感受一下:
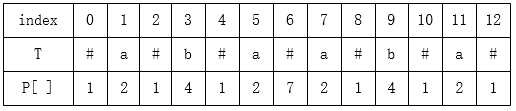
数组P有一性质,P[ i ]-1就是该回文子串在原字符串S中的长度 ,那就是P[i]-1就是该回文子串在原字符串S中的长度,至于证明,首先在转换得到的字符串T中,所有的回文字串的长度都为奇数,那么对于以T[i]为中心的最长回文字串,其长度就为2*P[i]-1,经过观察可知,T中所有的回文子串,其中分隔符的数量一定比其他字符的数量多1,也就是有P[i]个分隔符,剩下P[i]-1个字符来自原字符串,所以该回文串在原字符串中的长度就为P[i]-1。
另外,由于第一个和最后一个字符都是#号,且也需要搜索回文,为了防止越界,我们还需要在首尾再加上非#号字符,实际操作时我们只需给开头加上个非#号字符,结尾不用加的原因是字符串的结尾标识为‘\0‘,等于默认加过了。
1 //设t为将要进行预处理的字符串,则处理实现如下 2 string t="@#"; 3 for(int i=0;i<str.size();i++) 4 { 5 t=t+str[i]; 6 t=t+"#"; 7 }
这样原问题就转化成如何求数组P[ ]的问题了。
三)如何求数组P [ ]
三)如何求数组P [ ]
从左往右计算数组P[ ], Mi为之前取得最大回文串的中心位置,而R是最大回文串能到达的最右端的值。
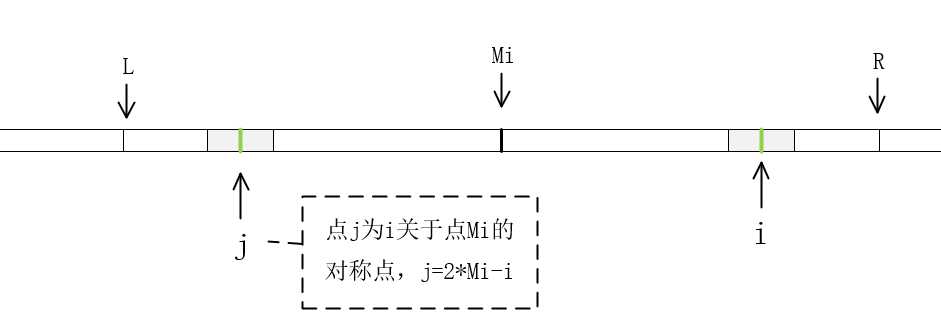
1)当 i <=R时,如何计算 P[ i ]的值了?毫无疑问的是数组P中点 i 之前点对应的值都已经计算出来了。利用回文串的特性,我们找到点 i 关于 Mi 的对称点 j ,其值为 j= 2*Mi-i 。因,点 j 、i 在以Mi 为中心的最大回文串的范围内([L ,R]),
a)那么如果P[j] <R-i (同样是L和j 之间的距离),说明,以点 j 为中心的回文串没有超出范围[L ,R],由回文串的特性可知,从左右两端向Mi遍历,两端对应的字符都是相等的。所以P[ j ]=P[ i ](这里得先从点j转到点i 的情况),如下图:
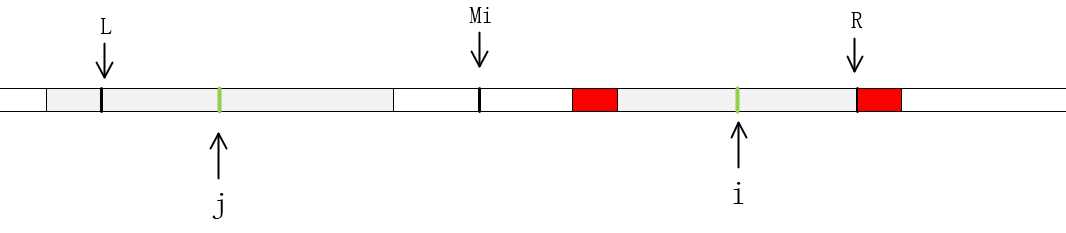
b)如果P[ j ]>=R-i (即 j 为中心的回文串的最左端超过 L),如下图所示。即,以点 j为中心的最大回文串的范围已经超出了范围[L ,R] ,这种情况,等式P[ j ]=P[ i ]还成立吗?显然不总是成立的!因,以点 j 为中心的回文串的最左端超过L,那么在[ L, j ]之间的字符肯定能在( j, Mi ]找到相等的,由回文串的特性可知,P[ i ] 至少等于R- i,至于是否大于R-i(图中红色的部分),我们还要从R+1开始一一的匹配,直达失配为止,从而更新R和对应的Mi以及P[ i ]。
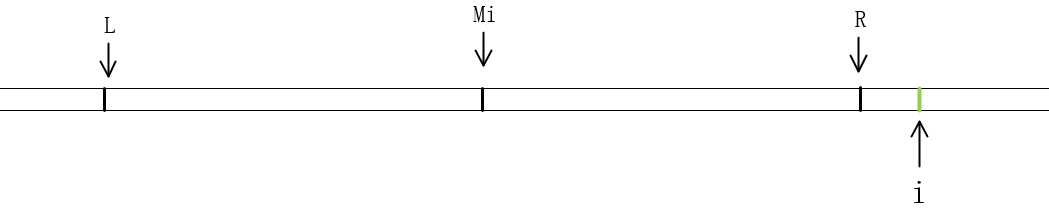
2)当 i > R时,如下图。这种情况,没法利用到回文串的特性,只能老老实实的一步步去匹配。
相应的代码如下:
1 string Manacher(string s) 2 { 3 /*改造字符串*/ 4 string res="$#"; 5 for(int i=0;i<s.size();++i) 6 { 7 res+=s[i]; 8 res+="#"; 9 } 10 11 /*数组*/ 12 vector<int> P(res.size(),0); 13 int mi=0,right=0; //mi为最大回文串对应的中心点,right为该回文串能达到的最右端的值 14 int maxLen=0,maxPoint=0; //maxLen为最大回文串的长度,maxPoint为记录中心点 15 16 for(int i=1;i<res.size();++i) 17 { 18 P[i]=right>i ?min(P[2*mi-i],right-i):1; //关键句,文中对这句以详细讲解 19 20 while(res[i+P[i]]==res[i-P[i]]) 21 ++P[i]; 22 23 if(right<i+P[i]) //超过之前的最右端,则改变中心点和对应的最右端 24 { 25 right=i+P[i]; 26 mi=i; 27 } 28 29 if(maxLen<P[i]) //更新最大回文串的长度,并记下此时的点 30 { 31 maxLen=P[i]; 32 maxPoint=i; 33 } 34 } 35 return s.substr((maxPoint-maxLen)/2,maxLen-1); 36 }
原文地址:https://www.cnblogs.com/love-yh/p/7072161.html
标签:默认 最长回文子串 lan size 大于 开始 www 半径 man
原文地址:https://www.cnblogs.com/jiamian/p/11251563.html