标签:顺序 cas 实例 构造 中继 width 市场 ast 路径
在机器学习中,决策树是一个预测模型;他代表的是对象属性与对象值之间的一种映射关系。树中每个节点表示某个对象,而每个分叉路径则代表的某个可能的属性值,而每个叶结点则对应从根节点到该叶节点所经历的路径所表示的对象的值。决策树仅有单一输出,若欲有复数输出,可以建立独立的决策树以处理不同输出。数据挖掘中决策树是一种经常要用到的技术,可以用于分析数据,同样也可以用来作预测。从根节点开始一步步走到叶子节点(决策),所有的数据最终都会落到叶子节点,既可以做分类也可以做回归。
例如对下面的5个小人儿根据年龄性别来进行构造出一棵决策树。
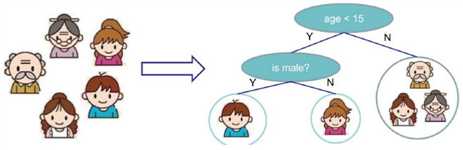
(1)根节点:表示第一个选择点.
(2)非叶子节点与分支:表示中间过程。
(3)叶子节点:表示最终的决策结果,所有的节点合起来就是整个数据集。。
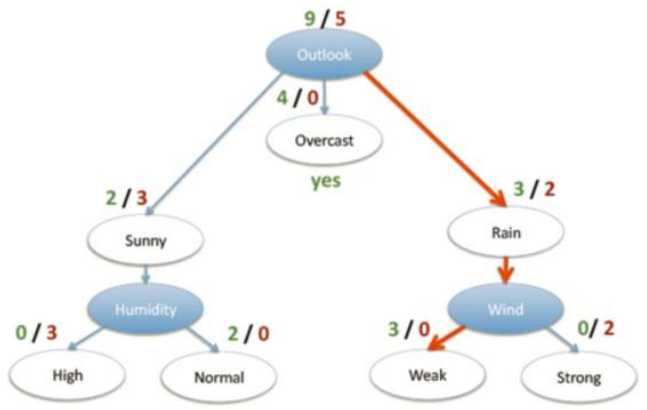
训练阶段:从给定的训练集构造出来一棵树(从根节点开始选择特征)
测试阶段:根据构造出来的树模型从上到下去走一遍就好了。
难点:一旦构造好了决策树,那么分类或者预测任务就很简单了,只需要走一遍就可以了,那么难点就在于如何构造出来一棵树,这就没那么容易了,需要考虑的问题很多。
问题:根节点的选择该用哪个特征呢?接下来呢?如何切分呢?
想象一下:我们的目标应该是根节点就像一个老大似的能更好的切分数据(分类的效果更好),根节点下面的节点自然就是老二了。
目标:那怎么去选择这个根节点呢? 我们可以通过一种衡量标准,来计算通过不同特征进行分支选择后的分类情况,找出来最好的那个根节点,以此类推。
熵:熵是表示随机变量不确定性的度量。(解释:说白了就是物体内部的混乱程度,比如杂货市场里面什么都有那肯定混乱呀,专卖店里面只卖一个牌子那就稳定多啦)。用公式来表达就是:H(X) = -ΣP(i)*log(p(i)),i = 1,2,3,...,n,log函数的底数是几无所谓。
公式解释:P(i)表示取到一个节点的概率。那么在log(p(i))函数中,如果P(i)的值越大,那么log(p(i))的值必然越接近于0,这时我们注意到公式前面还有个负号,所以H(X)值就越小,所以就表示熵值很小。综合起来说的话,就是概率P(i)的值越大,那么熵值越小,概率P(i)的值越小,那么熵值越大。下面通过一个栗子在来看看这个熵值,有下面A、B两个集合数据,判断一下两个集合的熵值情况。
A集合[1,1,1,1,1,1,1,1,2,2]
B集合[1,2,3,4,5,6,7,8,9,1]
显然A集合的熵值要低,因为A里面只有两种类别,相对稳定一些。而B中类别太多了,熵值就会大很多。(在分类任务中我们希望通过节点分支后数据类别的熵值大还是小呢?显示希望分支过后熵值越低越好)
那么如何选择一个节点呢?一般都是通过信息增益来进行节点的选择
表示特征X使得类Y的不确定性减少的程度。(分类后的专一性,希望分类后的结果是同类在一起)。假如原来熵值等于10,经过一次决策过后,熵值降低为8,那么信息增益值就等于2,那么我们可以遍历所有特征的熵值,看下哪个特征使我们的信息增益值最大,那么这个特征就是根节点。依次类推,再在剩下的特征中继续寻找信息增益值最大的特征,那么这个特征就是第二个节点了。
数据:14天打球情况
特征:4种环境变化,天气,温度,湿度,是否有风。
目标:构造决策树
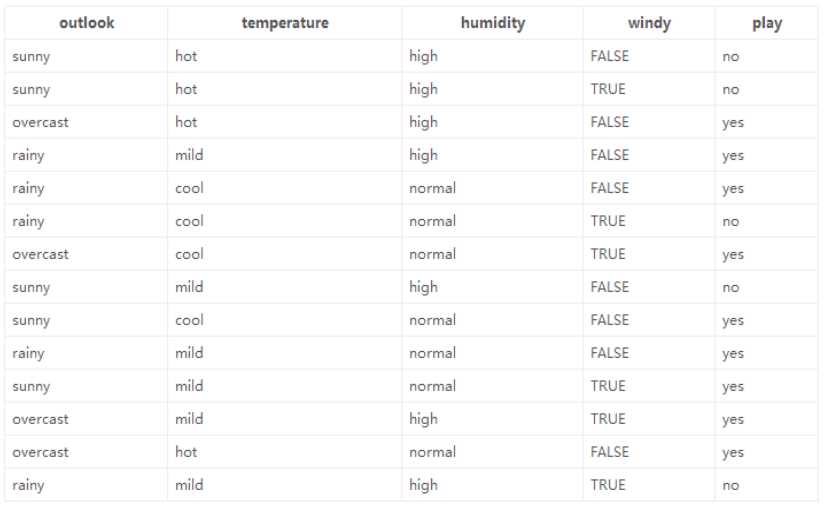
划分方式:因为数据总共四个特征,所以划分方式也是4种
问题:谁当根节点呢?,有如下四种划分。
依据:信息增益
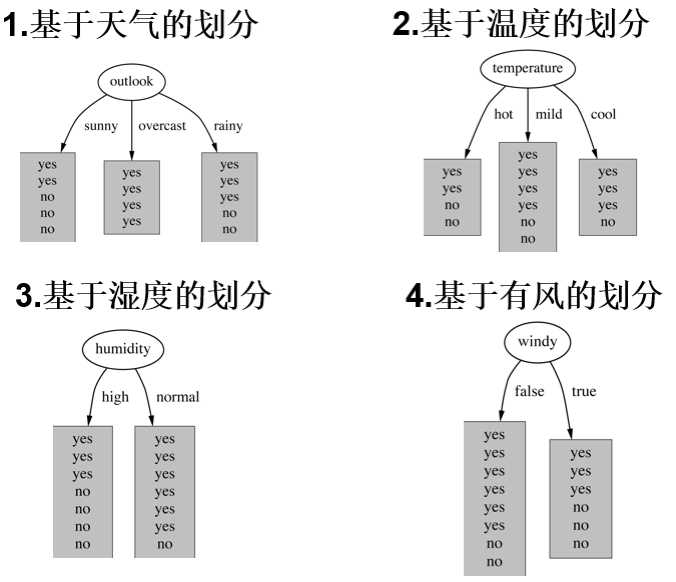
接下来通过计算来筛选哪个特征来当根节点。在历史数据中(14)天有9天打球,5天不打球,首先计算这14天中,是否打球这一特征的熵值为
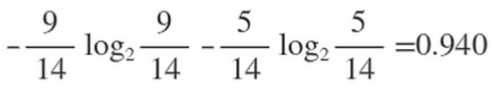
然后接下来对4个特征逐一分析,先从outlook特征开始:
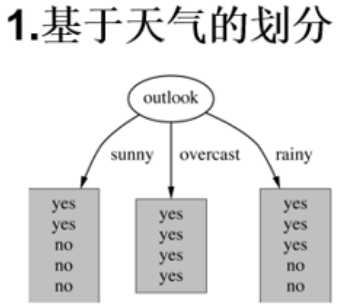
Outlook = sunny时,熵值为0.971,式子为-(2/5)*log2(2/5)-(3/5)*log2(3/5)。
Outlook = overcastt时,熵值为0,同理计算。
Outlook = rainy时,熵值为0.971,同理计算。
根据数据统计,outlook取值分别为sunny,overcast,rainy的概率分别为:5/14, 4/14, 5/14,所以最终如果我们以Outlook为根节点的话,它的熵值为:5/14 * 0.971 + 4/14 * 0 + 5/14 * 0.971 = 0.693
那么如果我们选择以Outlook为根节点的话,首先系统最初的熵值为0.940,下降到Outlook的熵值的话,那么信息增益的值就为0.247,用gain(Outlook)=0.247表示。同理我们可以计算出其他特征的信息增益值,gain(temperature)=0.029 gain(humidity)=0.152 gain(windy)=0.048。那么我们选择最大的那个就可以啦,相当于是遍历了一遍特征,找出来了根节点老大也就是Outlook特征,然后在其余的中继续通过信息增益就可以找到老二等等。
ID3:信息增益(有什么问题呢?),假如数据集里面有个ID的特征,如果通过这个特征来进行划分,那么ID这个特征的熵值为0,那么此时信息增益值就是最大的,所以根节点就是ID这个特征了,那这个划分肯定是不可取的。所以ID3这个算法的问题就是,如果某个特征非常稀疏,里面属性值又比较小,那么这个特征的熵值就比较小,信息增益就比较大了。
C4.5:信息增益率(解决ID3问题,考虑自身熵):信息增益率=信息增益/自身熵值。
CART:使用GINI系数来当做衡量标准,GINI系数,和熵的衡量标准类似,计算方式不相同)
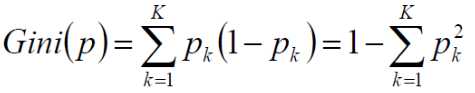
为什么要剪枝:决策树过拟合风险很大,理论上可以完全分得开数据(想象一下,如果树足够庞大,每个叶子节点不就一个数据了嘛),剪枝的策略可以把它想象成小区里面给树木剪枝的操作。
剪枝策略:预剪枝,后剪枝
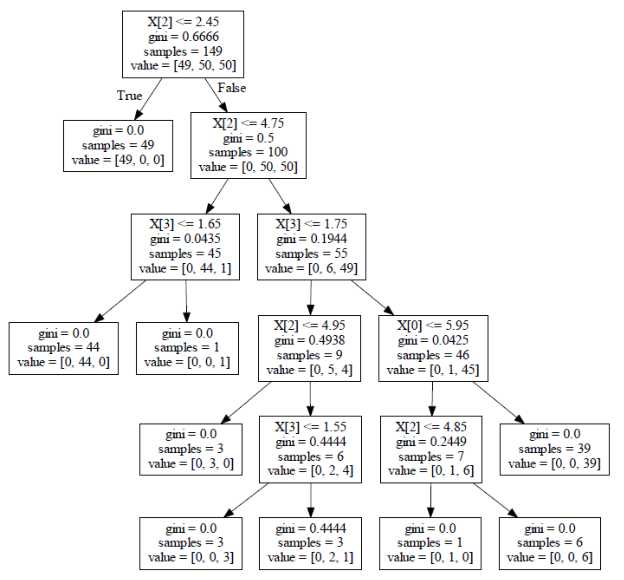
预剪枝:边建立决策树边进行剪枝的操作(更实用),限制决策树深度,叶子节点个数,叶子节点样本数,信息增益值等
后剪枝:当建立完决策树后来进行剪枝操作,通过一定的衡量标准Cα(T)=C(T)+α*|Tleaf|(叶子节点越多,损失越大),C(T)表示损失,等于样本数*熵值(gini系数),也就是上图中的samples*gini,Tleaf表示叶子节点的个数。α表示需要自己指定的参数。
优点:决策树易于理解和实现,在相对短的时间内能够对大型数据源做出可行且效果良好的结果。能够直接体现数据的特点。
缺点:对连续性的字段比较难预测,对有时间,id等顺序的数据,需要做很多预处理的工作。
标签:顺序 cas 实例 构造 中继 width 市场 ast 路径
原文地址:https://www.cnblogs.com/xiaoyh/p/11219655.html