标签:scan == getc 结果 解决 inf 改变 break 遍历
粗略的讲一下这两种算法,为老年痴呆做好准备(ノへ ̄、)
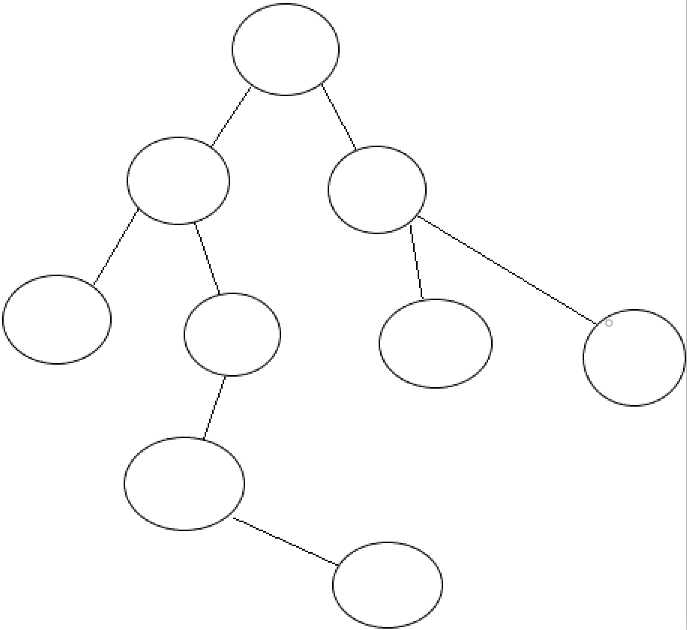
DFS:
如上图,你将搜索整张图,而DFS的搜索方法就是,先一味的往前走!走到某个尽头后发现无路可走,后退。咦?后退一步有一个分岔口,这里有多个支路,选择一条没走过的继续走,碰到死胡同,后退,又到了这个分岔口,再去选择没走过的路,直到无路可走,然后返回上一个分岔口。具体过程如下:
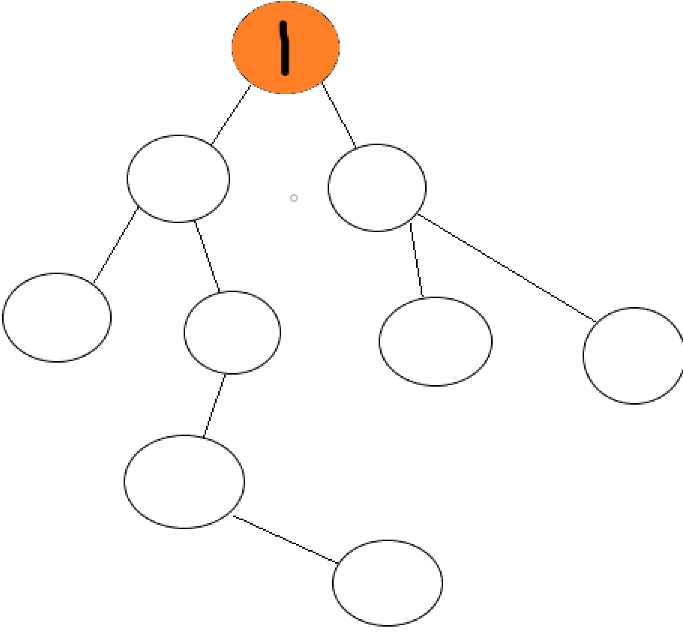
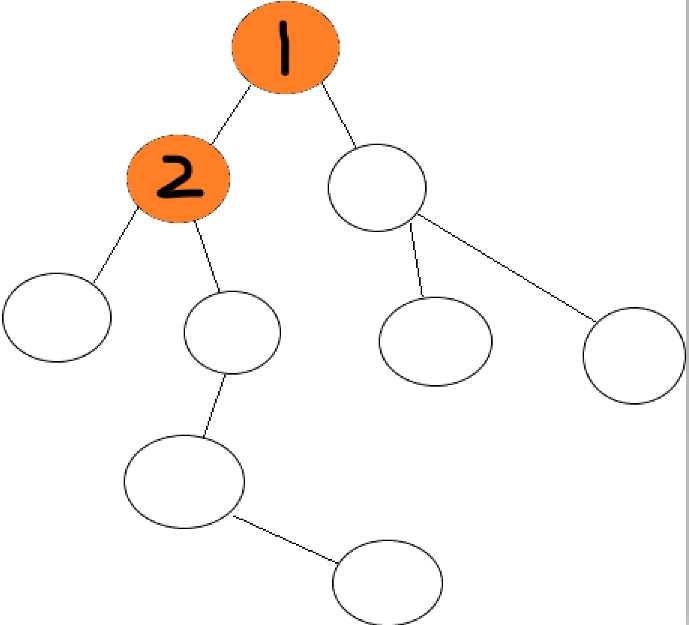
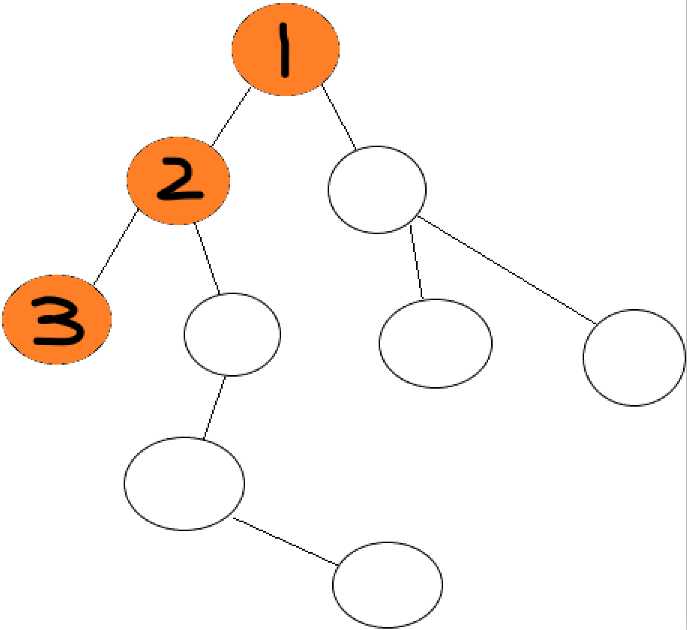
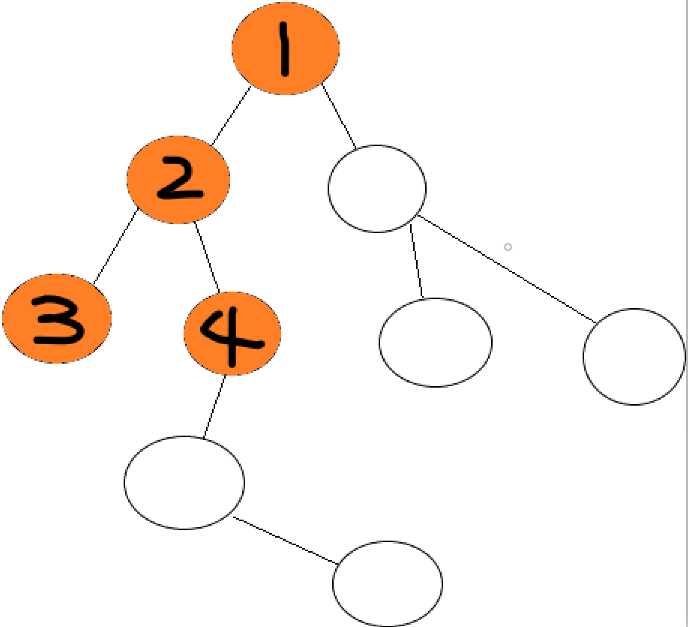
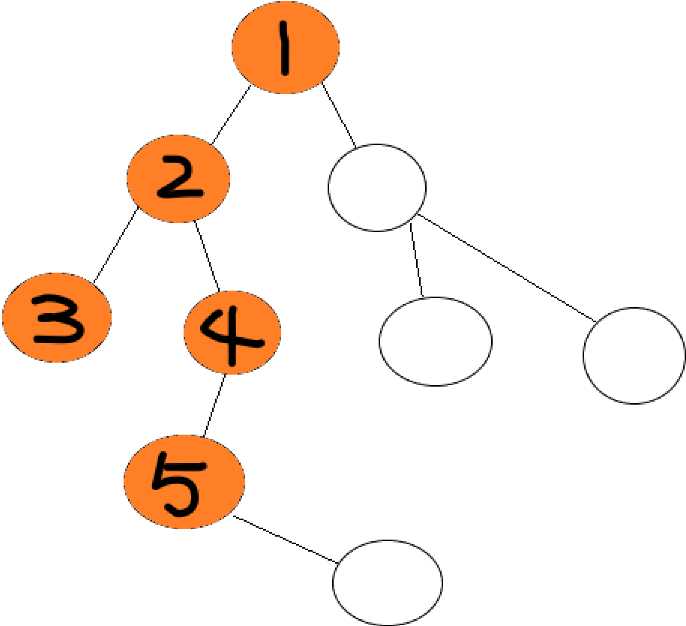
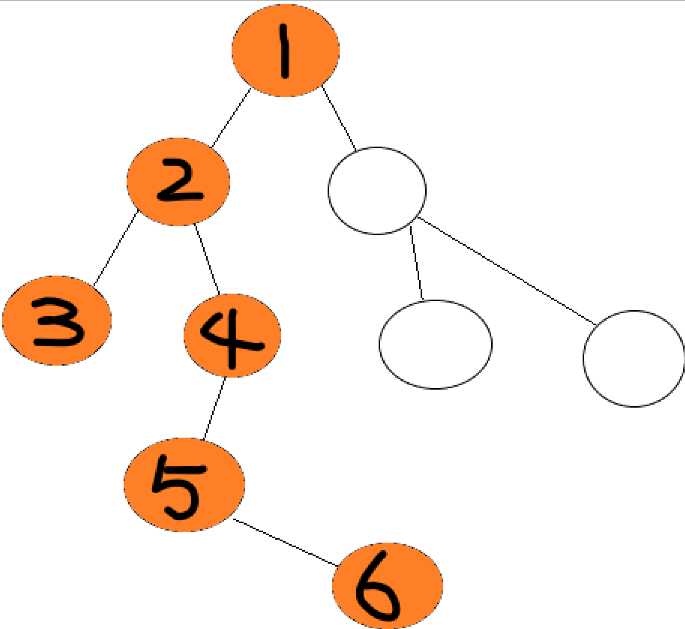
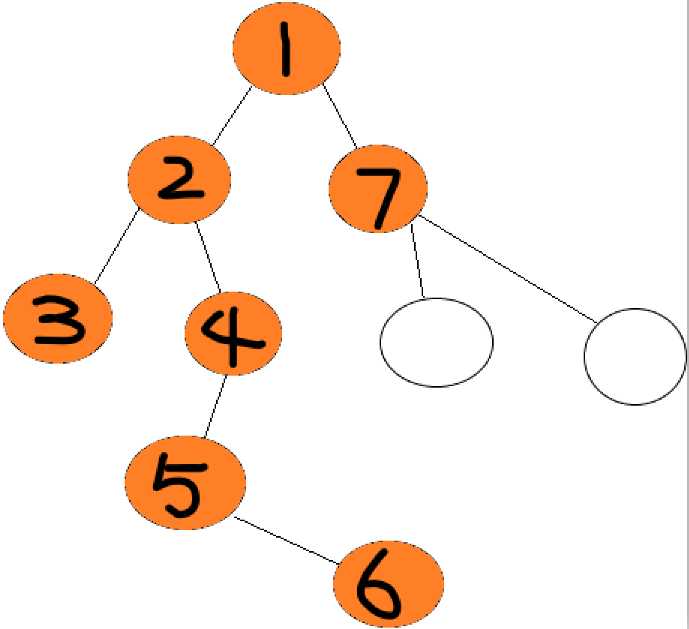
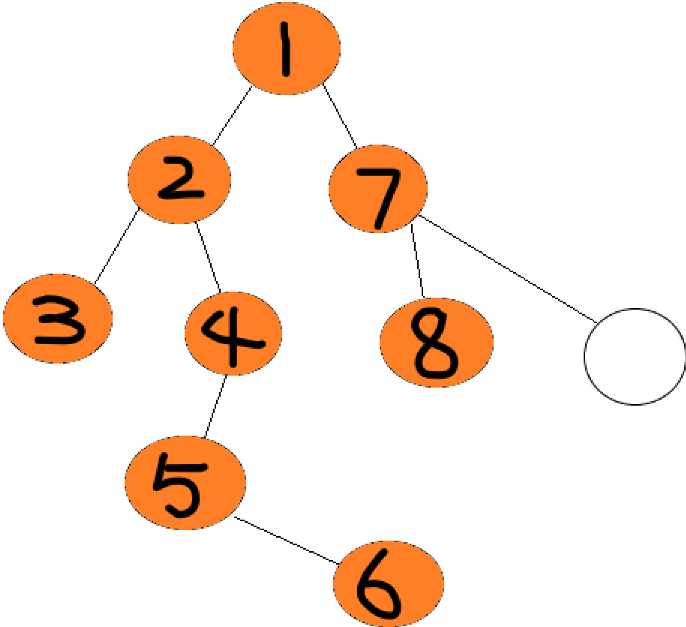
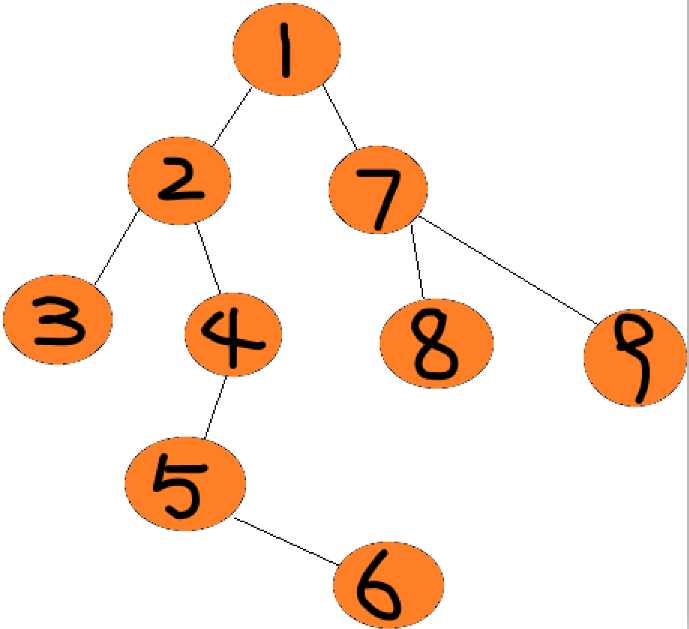
(图中黑色数字均为遍历顺序)
这样一遍历,就把整张图都走过了!不仅如此,起点不论放在哪里,都不会影响遍历整张图的结果。遍历对象也不限于上面的图,还有树,二维,三维矩阵等,总之,DFS思想十分重要。DFS算法适用于解决所有解问题和连通性问题。
BFS
不同于过于鲁莽的DFS,BFS总是优先于身边的各种支路,它一定是先把距离近的优先搜索完,然后逐渐加深层次。如下图的搜索顺序:
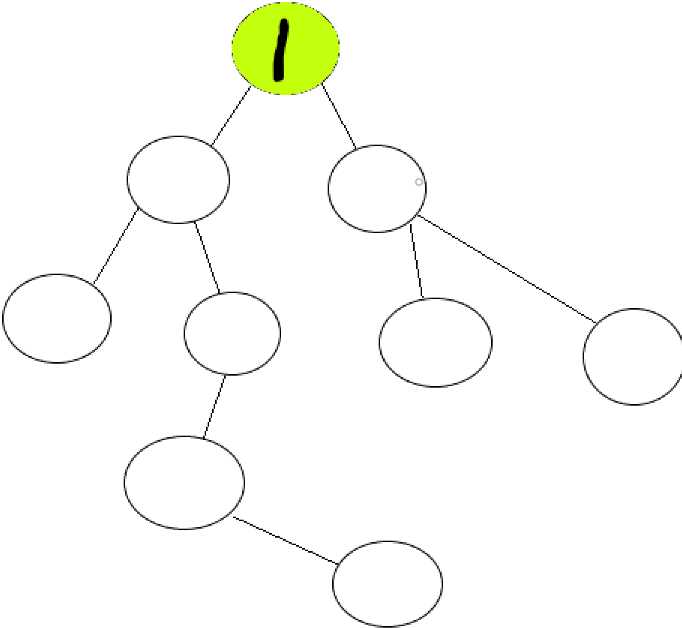
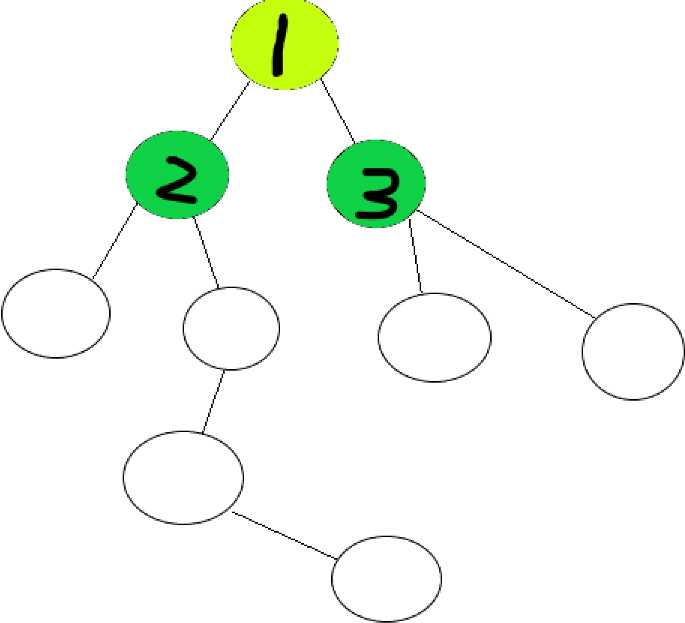
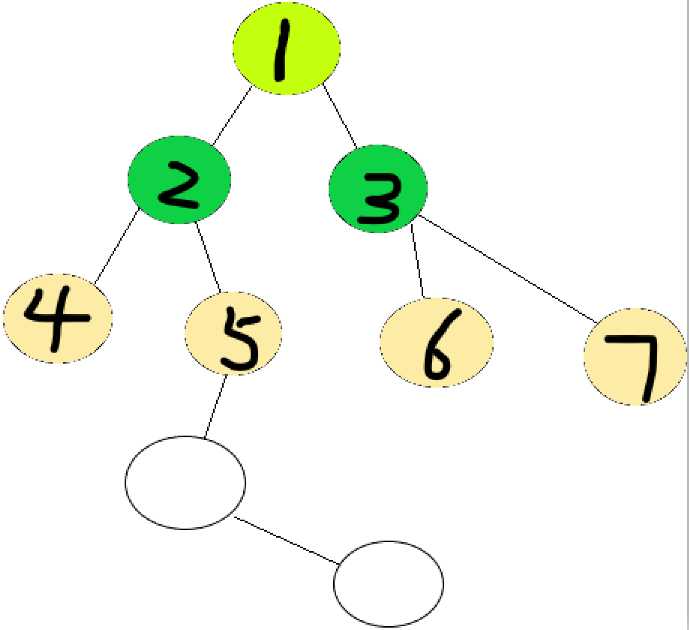
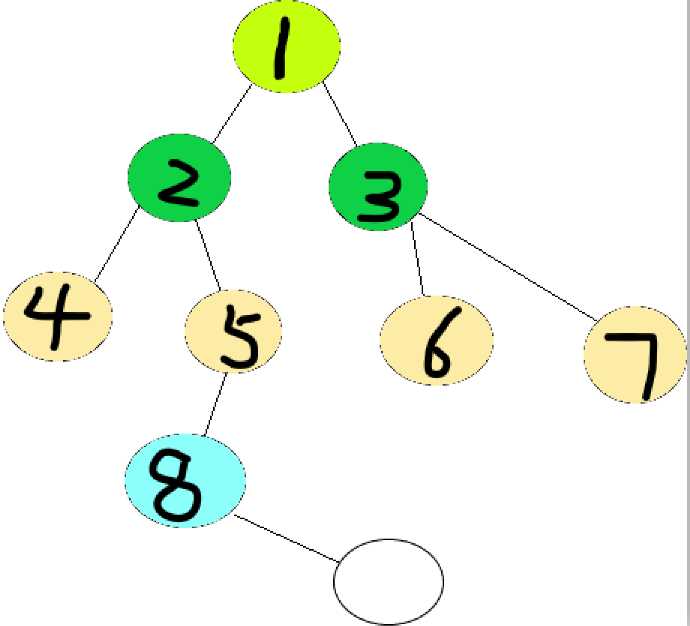
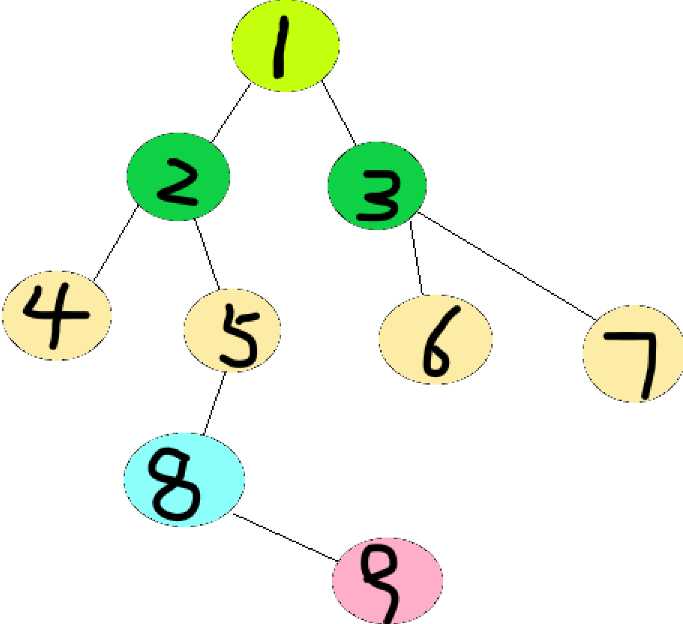
(不同颜色代表不同层次,黑色数字亦为搜索顺序)
BFS和DFS大多数时候相同,不同的是,BFS更倾向于解决最短路和最优解问题。其算法的实现依托于队列。(既可手动模拟队列,也可以使用queue)
代码将会在具体题目中给出。
DFS经典例题:POJ1321 棋盘问题;http://poj.org/problem?id=1321

#include<stdio.h> #include<string.h> int n,k,ans; char map[10][10];//棋盘地图 int vis[10];//标记棋子列位置是否已经访问 void dfs(int r,int k)//还有K枚棋子,从第R行开始遍历 { if(k==0)//如果手中没有棋子,遍历结束,方法数+1. { ans++; return; } for(int i=r;i<=n;i++) { for(int j=1;j<=n;j++) { if(map[i][j]==‘.‘||vis[j]==1)//如果某个位置不可走或者该列已经被访问,访问下一列. continue; vis[j]=1; dfs(i+1,k-1); vis[j]=0;//为什么此处位置又标记未被访问? 棋盘的棋子摆放位置是互相影响的, //这行棋子在这一种情况能摆这,另外的情况也能摆这,但不会重叠,因为下一次遍历到它的时候情况发生了改变 } } } int main(void) { while(scanf("%d %d",&n,&k)!=EOF) { getchar(); if(n==-1&&k==-1) break; memset(map,‘\0‘,sizeof(map));//棋盘清零 memset(vis,0,sizeof(vis));//访问清零 ans=0; for(int i=1;i<=n;i++) { for(int j=1;j<=n;j++) map[i][j]=getchar(); getchar(); } dfs(1,k);//表示还有K枚棋子,从第一行开始遍历 printf("%d\n",ans); } return 0; }
标签:scan == getc 结果 解决 inf 改变 break 遍历
原文地址:https://www.cnblogs.com/switch-waht/p/11272737.html