标签:otl 5* 需要 知识 ati lin 方法 情况 mamicode
//2019.08.02下午
#机器学习算法中的超参数与模型参数
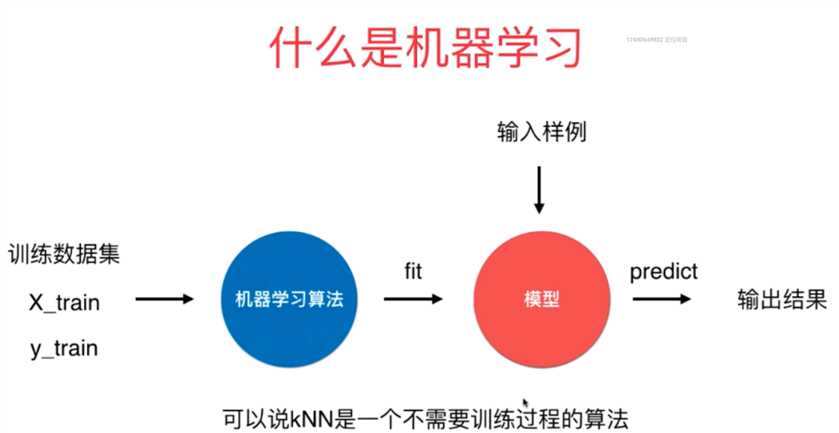
1、超参数:是指机器学习算法运行之前需要指定的参数,是指对于不同机器学习算法属性的决定参数。通常来说,人们所说的调参就是指调节超参数。
2、模型参数:是指算法在使用过程中需要学习得到的参数,即输入与输出之间映射函数中的参数,它需要通过对于训练数据集训练之后才可以得到。
3、对于KNN算法,它是没有模型参数的,它的k参数就属于典型的超参数。
4、好的超参数的选择主要取决于三个方面:
(1)领域知识
(2)经验数值
(3)实验搜索
5、K近邻算法常用的三大超参数:k、weights=("uniform","distance")以及在weights=distance的情况下p参数。
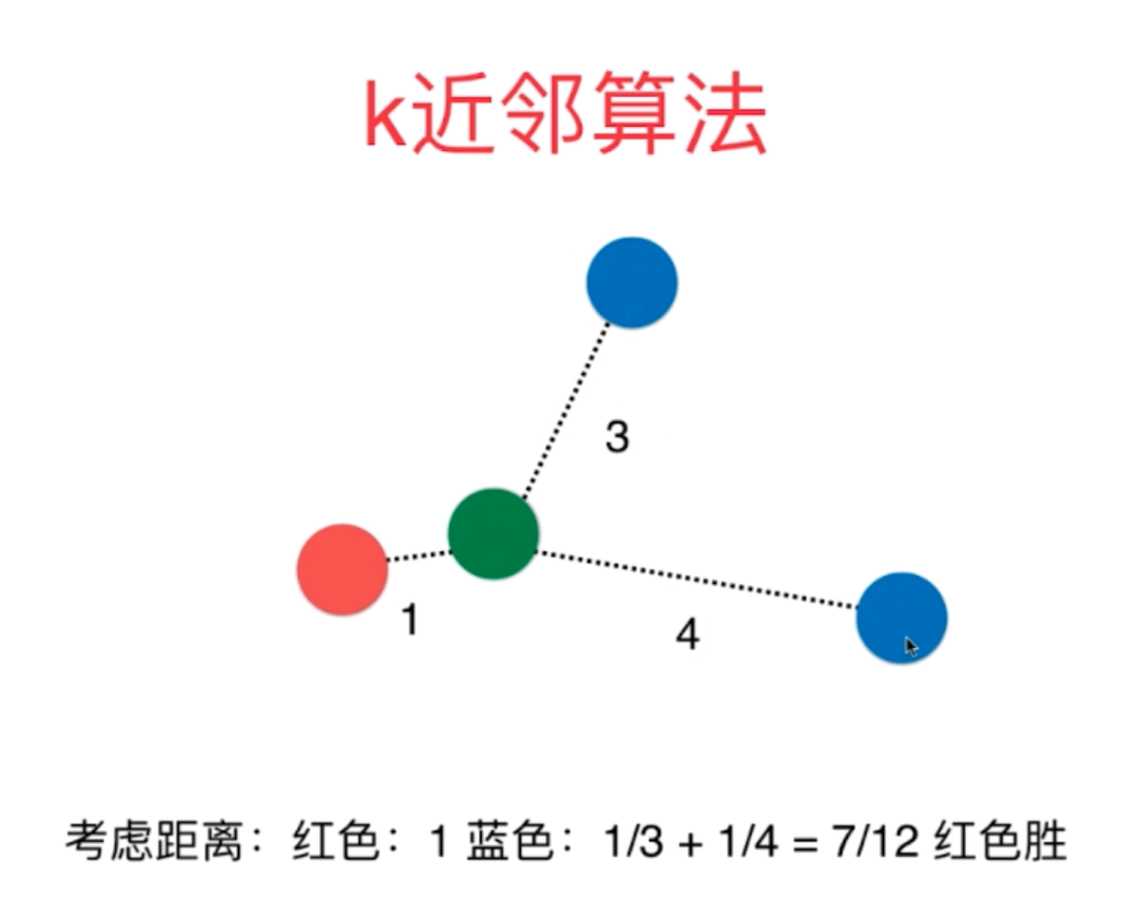

6、K近邻算法超参数调节寻找最优的方法:网络搜索方式举例如下:
#对于KNN算法寻找最佳的超参数k的值以及另外一个超参数weights=uniform/distances,以及在distance的情况下选择出最佳的超参数p的值的大小:
import numpy as np
import matplotlib.pyplot as plt #导入相应的数据可视化模块
#根据训练得到模型的准确率来进行寻找最佳超参数k肯weights
best_method=""
best_score=0.0
best_k=0
s=[] #初始定义所需要寻找的超参数
from sklearn.neighbors import KNeighborsClassifier
for method in ["uniform","distance"]:
for k in range(1,11): #采用for循环来进行寻找最优的超参数
KNN=KNeighborsClassifier(n_neighbors=k,weights=method)
KNN.fit(x_train,y_train) #进行原始数据的训练
score=KNN.score(x_test,y_test) #直接输出相应的准确度
s.append(score)
if score>best_score:
best_score=score
best_k=k
best_method=method
#数据验证
print("best_method=",best_method)
print("best_k=",best_k)
print("best_score=",best_score)
plt.figure(2)
x=[i for i in range(1,21)]
plt.plot(x,s,"r")
plt.show()
#根据训练得到模型的准确率来进行寻找最佳超参数k以及在weights=distance的情况下寻找最优的参数p
best_p=0
best_score=0.0
best_k=0
s=[] #初始化超参数
from sklearn.neighbors import KNeighborsClassifier
for k in range(1,11):
for p in range(1,6):
KNN=KNeighborsClassifier(n_neighbors=k,weights="distance",p=p)
KNN.fit(x_train,y_train) #进行原始数据的训练
score=KNN.score(x_test,y_test) #直接输出相应的准确度
s.append(score)
if score>best_score:
best_score=score #利用网络搜索方式来寻找最高准确率下的最佳超参数
best_k=k
best_p=p
#数据验证
print("best_p=",best_p)
print("best_k=",best_k)
print("best_score=",best_score)
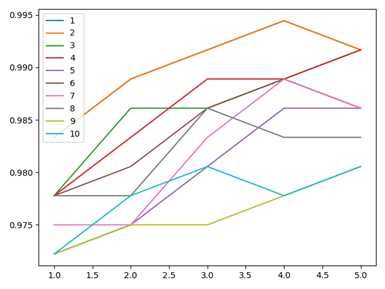
plt.figure(2)
s1=[]
x=[i for i in range(1,6)]
for i in range(1,11):
s1=s[(i*5-5):(5*i)]
plt.plot(x,s1,label=i)
plt.legend(loc=2)
plt.show()
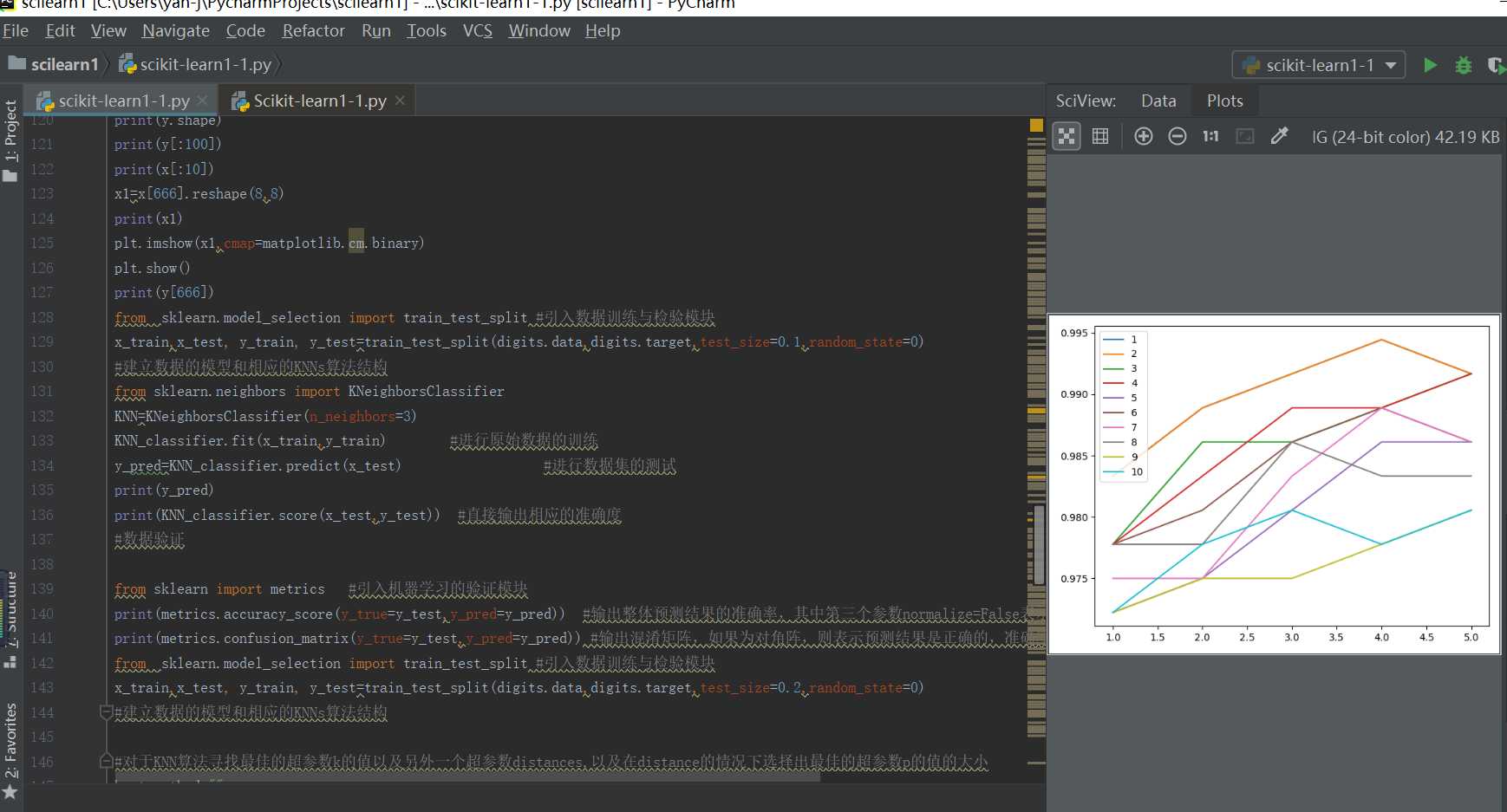
输出结果如下所示:(不同的k和p参数情况下的准确度输出结果)
标签:otl 5* 需要 知识 ati lin 方法 情况 mamicode
原文地址:https://www.cnblogs.com/Yanjy-OnlyOne/p/11294633.html