标签:att 不同 index alt 数据 RKE style 图片 比较
在scikit-learn中,包括两个K-Means的算法,:
(1)传统的K-Means算法,对应的类是KMeans。
(2)基于采样的Mini Batch K-Means算法,对应的类是MiniBatchKMeans。
一般来说,K-Means的算法调参是比较简单的,虽然KMeans类和MiniBatchKMeans类可以选择的参数并不少,但是大多不太需要去调参。:
(1)用KMeans,一般要注意的仅仅就是k值的选择,即参数n_clusters;
(2)用MiniBatchKMeans,一般注意n_clusters和batch_size(即采样的数量)
1、KMeans类的主要参数有:
1) n_clusters: 即我们的k值,一般需要多试一些值以获得较好的聚类效果。k值好坏的评估标准在下面会讲。
2)max_iter: 最大的迭代次数,一般如果是凸数据集的话可以不管这个值,如果数据集不是凸的,可能很难收敛,此时可以指定最大的迭代次数让算法可以及时退出循环。
3)n_init:用不同的初始化质心运行算法的次数。由于K-Means是结果受初始值影响的局部最优的迭代算法,因此需要多跑几次以选择一个较好的聚类效果,默认是10,一般不需要改。如果你的k值较大,则可以适当增大这个值。
4)init: 即初始值选择的方式,可以为完全随机选择‘random‘,优化过的‘k-means++‘或者自己指定初始化的k个质心。一般建议使用默认的‘k-means++‘。
5)algorithm:有“auto”, “full” or “elkan”三种选择。"full"就是我们传统的K-Means算法, “elkan”是我们原理篇讲的elkan K-Means算法。默认的"auto"则会根据数据值是否是稀疏的,来决定如何选择"full"和“elkan”。一般数据是稠密的,那么就是 “elkan”,否则就是"full"。一般来说建议直接用默认的"auto"
2、MiniBatchKMeans类的主要参数比KMeans类稍多,主要有:
1) n_clusters: 即我们的k值,和KMeans类的n_clusters意义一样。
2)max_iter:最大的迭代次数, 和KMeans类的max_iter意义一样。
3)n_init:用不同的初始化质心运行算法的次数。这里和KMeans类意义稍有不同,KMeans类里的n_init是用同样的训练集数据来跑不同的初始化质心从而运行算法。而MiniBatchKMeans类的n_init则是每次用不一样的采样数据集来跑不同的初始化质心运行算法。
4)batch_size:即用来跑Mini Batch KMeans算法的采样集的大小,默认是100.如果发现数据集的类别较多或者噪音点较多,需要增加这个值以达到较好的聚类效果。
5)init: 即初始值选择的方式,和KMeans类的init意义一样。
6)init_size: 用来做质心初始值候选的样本个数,默认是batch_size的3倍,一般用默认值就可以了。
7)reassignment_ratio: 某个类别质心被重新赋值的最大次数比例,这个和max_iter一样是为了控制算法运行时间的。这个比例是占样本总数的比例,乘以样本总数就得到了每个类别质心可以重新赋值的次数。如果取值较高的话算法收敛时间可能会增加,尤其是那些暂时拥有样本数较少的质心。默认是0.01。如果数据量不是超大的话,比如1w以下,建议使用默认值。如果数据量超过1w,类别又比较多,可能需要适当减少这个比例值。具体要根据训练集来决定。
8)max_no_improvement:即连续多少个Mini Batch没有改善聚类效果的话,就停止算法, 和reassignment_ratio, max_iter一样是为了控制算法运行时间的。默认是10.一般用默认值就足够了。
不像监督学习的分类问题和回归问题,无监督聚类没有样本输出,也就没有比较直接的聚类评估方法,但是可以从簇内的稠密程度和簇间的离散程度来评估聚类的效果。
常见的评价方法:(1)轮廓系数Silhouette Coefficient
(2)Calinski-Harabasz Index。
Calinski-Harabasz Index计算简单直接,数学计算公式是:
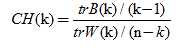
n表示聚类的数目 ,k 表示当前的类, trB(k)表示类间协方差矩阵的迹, trW(k) 表示类协方差矩阵的迹
得到的Calinski-Harabasz分数值CH(K)越大则聚类效果越好。其中,类别内部数据的协方差越小越好,类别之间的协方差越大越好,这样的Calinski-Harabasz分数会高。
在scikit-learn中, Calinski-Harabasz Index对应的方法是metrics.calinski_harabaz_score.
下面用KMeans类和MiniBatchKMeans类聚类,并观察比较在不同的k值下Calinski-Harabasz分数。
(1)随机创建一些二维数据作为训练集,代码如下:
import numpy as np import matplotlib.pyplot as plt %matplotlib inline from sklearn.datasets.samples_generator import make_blobs # X为样本特征,Y为样本簇类别, 共1000个样本,每个样本2个特征,共4个簇,簇中心在[-1,-1], [0,0],[1,1], [2,2], 簇方差分别为[0.4, 0.2, 0.2] X, y = make_blobs(n_samples=1000, n_features=2, centers=[[-1,-1], [0,0], [1,1], [2,2]], cluster_std=[0.4, 0.2, 0.2, 0.2], random_state =9) plt.scatter(X[:, 0], X[:, 1], marker=‘o‘) plt.show()
(2)用K-Means聚类方法来做聚类,首先选择k=2,代码如下:
from sklearn.cluster import KMeans y_pred = KMeans(n_clusters=2, random_state=9).fit_predict(X) plt.scatter(X[:, 0], X[:, 1], c=y_pred) plt.show()
用Calinski-Harabasz Index评估的聚类分数: 3116.1706763322227
rom sklearn import metrics
metrics.calinski_harabaz_score(X, y_pred)
(3)k=3时候的聚类
from sklearn.cluster import KMeans y_pred = KMeans(n_clusters=3, random_state=9).fit_predict(X) plt.scatter(X[:, 0], X[:, 1], c=y_pred) plt.show()
Calinski-Harabaz Index评估的k=3时候聚类分数: 2931.625030199556
metrics.calinski_harabaz_score(X, y_pred)
(4)k=4时候的聚类
from sklearn.cluster import KMeans y_pred = KMeans(n_clusters=4, random_state=9).fit_predict(X) plt.scatter(X[:, 0], X[:, 1], c=y_pred) plt.show()
Calinski-Harabaz Index评估的k=4时候聚类分数: 5924.050613480169
k=4的聚类分数比k=2和k=3都要高,符合预期,最终选择分为4个簇。
所以,当特征维度大于2,无法直观可视化观察聚类效果时,用Calinski-Harabaz Index评估是一个很方便有效的方法。
(5)用MiniBatchKMeans的效果,将batch size设置为200. 由于我们的4个簇都是凸的,所以其实batch_size的值只要不是非常的小,对聚类的效果影响不大。
for index, k in enumerate((2,3,4,5)): plt.subplot(2,2,index+1) y_pred = MiniBatchKMeans(n_clusters=k, batch_size = 200, random_state=9).fit_predict(X) score= metrics.calinski_harabaz_score(X, y_pred) plt.scatter(X[:, 0], X[:, 1], c=y_pred) plt.text(.99, .01, (‘k=%d, score: %.2f‘ % (k,score)), transform=plt.gca().transAxes, size=10, horizontalalignment=‘right‘) plt.show()
使用MiniBatchKMeans的聚类效果也不错,KMeans类的Calinski-Harabasz Index分数为5924.05,而MiniBatchKMeans的分数稍微低一些,为5921.45。这个差异损耗并不大。
标签:att 不同 index alt 数据 RKE style 图片 比较
原文地址:https://www.cnblogs.com/wl413911/p/11324155.html