标签:ef6 公共前缀 不用 依次 回顾 计数排序 cat print 怎么
后缀数组,顾名思义,就是对于一个字符串的每一个后缀的数组。
比如对于字符串fatcat,其所有后缀如下:
fatcat
atcat
tcat
cat
at
t
其按照字典序排序结果如下:
at
atcat
cat
fatcat
t
tcat
一般来说,对于每个后缀,要求的数组有3个:
后缀数组有用的部分是height[],核心是求sa[]。
求sa[]需要用到倍增法。
假设已经求出长度为k的字符串排序后的数组,可以通过合并求出长度为2k的。
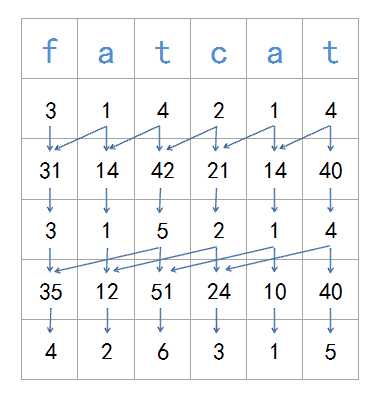
每次合并i和i+2^k(k=0~…)。比如上图中第二次,3代表(1,2),5代表(3,4),35就代表(1,2,3,4)。
单次排序复杂度为O(N),每次长度扩大一倍,共需扩大logN次。总的时间复杂度为O(NlogN)
桶排序(bucket sort)是怎么排的?
因为我喜欢buck,所以把桶叫做buck[]
类似计数排序,首先要知道每种数有几个。
然后用前缀和的方式,比如1,1,4,5,1,4,
先枚举每一位,相应的buck[s[i]]++。得到buck[1] = 3,buck[4] = 2,buck[5] = 1。
然后求前缀和,得到buck[1] = 3,buck[4] = 5,buck[5] = 6。
那么可以发现,buck[i]对应的恰好是当前的数的最后一个的排名(1,1,1,4,4,5)。
有了这些前置知识,后缀数组就很容易(?)解决了。
定义变量
这里说的“后缀序号”就是后缀开头的元素在字符串中的序号。
int buck[]; 桶,表示装rk[i]的元素的桶
int sa[]; rk[i]的后缀序号
int rk[]; 序号为i后缀的排名
int trk[]; 临时排名,因为每次循环的rk是留着有用的不能改qwq
int hgt[]; rk[]为i和i-1的后缀的LCP(最长公共前缀)长度
char s[]; 用来存字符串
int len,cnt; 字符串长度和当前排名的最后一位。
注意:
scanf("%s",s+1); int len = strlen(s+1); printf("%s",s+1);
$get$_$sa()$
1 for(int i = 1; i <= len; i++) buck[s[i]]++; 2 for(int i = 0; i <= 122; i++) if(buck[i]) trk[i] = ++cnt; 3 for(int i = 1; i <= 122; i++) buck[i] += buck[i-1]; 4 for(int i = 1; i <= len; i++) { 5 rk[i] = trk[s[i]]; 6 sa[buck[s[i]]--] = i; 7 } 8 for(int k = 1; cnt != len; k <<= 1) { 9 cnt = 0; 10 for(int i = 0; i <= len; i++) buck[i] = 0; 11 for(int i = 1; i <= len; i++) buck[rk[i]]++; 12 for(int i = 1; i <= len; i++) buck[i] += buck[i-1]; 13 for(int i = len; i; i--) 14 if(sa[i] > k) trk[sa[i]-k] = buck[rk[sa[i]-k]]--; 15 for(int i = len; i >= len-k+1; i--) 16 trk[i] = buck[rk[i]]--; 17 for(int i = 1; i <= len; i++) sa[trk[i]] = i; 18 for(int i = 1; i <= len; i++) trk[sa[i]] = Ssame(sa[i],sa[i-1],k) ? cnt : ++cnt; 19 for(int i = 1; i <= len; i++) rk[i] = trk[i]; 20 }
为了方便看,加上行号qwq
这个东西我从十二点看到三点半也没看懂(虽然一遍摸鱼一边看)
这个函数分为两部分:初始化、循环。
初始化(1~7):
1.遍历字符串,将字符加入桶。
2.因为模板题是‘0‘~‘z‘,‘z‘的ascii码是122。那么看看每一种字符是否存在,可以得到初步排名。
这里trk[i]指字符i离散化后的排名。这样排的名,因为只排了1位,所以很有可能有重复。
3.桶排序求前缀和的步骤(见上文)。
4-7.对于字符串的每一位,看看它所对应的字符s[i]的排名是多少,就能得到字符串第i位的排名rk[i];
排名buck[s[i]](见上文)所对应的的后缀序号即为i;
因为要找排名为k的序号sa[k],排名不能空着;比如114514→111445不能只有sa[3],sa[5],s[6],所以要把sa填满。buck[s[i]]-1,即减少一个元素,那么即使排名k-1不存在,sa[k-1]也能被填上。这样第一个1填充sa[3],第二个1填充sa[2],依次类推。后文把这个"排名"加上双引号,和真实排名区分。
注意,rk的大小还是有重复的,只是sa被填满了而已。还用刚刚的例子,
sa[2("排名"为2)]=2(序号为2,即第二个1),但rk[2(序号为2)]=1(排名为1)。
循环(8~20):
8.倍增,从1开始枚举k,每次k*=2,表示排序选取比较的长度为2^k。
cnt==len时,说明没有重复的排名了,这时就完成了排序,退出循环。
9.cnt表示最大的排名,先清零。
10.清空桶。因为桶是基于rk[]的,初始化离散后,最大不会超过len,所以就不用枚举到122了。
11.遍历字符串。加入桶的是第i位的排名(是初始化或上次循环离散化后、有重复的)。
12.处理桶的前缀和。
13-14.这里的len~1表示"排名"。
这里要求的是:假设有后缀p,"排名"为i的作为第二关键字,按第一关键字排序的新"排名"。
回顾一下第6行:sa[i]是rk为i的序号,而且虽然有些排名不存在,但sa["排名"]都被填满了。
那么,sa[i]是第二关键字的序号,sa[i]-k就是第一关键字的序号。从len到1枚举,保证了第二关键字的"排名"一定是从后往前的。
但是,如果sa[i]在第k位或之前,它就不可能作为第二关键字了,所以要先判断(sa[i] > k)。
方便后面遍历,新"排名"也要填充成1~len,所以buck[]-1。
这个新"排名"要存在临时的trk中。(我都快不认识排名两个字了)。
15-16.这里的len~len-k+1表示后缀序号。
前k位不能作为第二关键字,相应的,后k位(len~len-k+1)没有第二关键字,也就相当于第二关键字为0。第二关键字为0的,在相同的第一关键字中排在最前面,它们的buck[]也就是把前面的都减去后,在相同的第一关键字中最小的。
(最难的地方已经过去了!)
17.按新"排名"trk[],把sa[]重新对应。
18.求出真正的新排名,也就是离散化trk[]——判断每个新"排名"trk[]是否真的不同,需要用到一个函数Ssame()。
$Ssame()$
bool Ssame(int a,int b,int k) { if(a+k > len || b+k > len) return false; return (rk[a] == rk[b]) && (rk[a+k] == rk[b+k]); }
求分别以第a,b位为第一关键字,第a+k,b+k位为第二关键字的两个后缀是否真的不同。
如果某一个+k后超过了len,那这两个后缀的长度肯定不同,而且如果第一关键字相同了,短的一定在前。不用想,直接返回false;
不然的话,看看上一次排出的真正排名。如果两个位置上的数是一样的,那真正的排名肯定是一样的。如果两个后缀的第一关键字的排名(rk[a],rk[b])和第二关键字的排名(rk[a+k],rk[b+k])都一样,那么很不幸,目前为止,这两个后缀还是一样的,返回true;否则false。
很显然,如果"排名"为i-1的后缀和"排名"为i的后缀都不同,那么"排名"为i-1的和i+1的一定不同。
所以,每次只要比较"排名"为i-1和i的就可以了。第一关键字的序号是sa[i],sa[i-1],第二关键字就是这两个+k。
如果i和i-1相同,那么真排名也相同,i的排名还是cnt不变;否则是++cnt。
19.把用刚刚求好的新排名trk[]更新rk[]。
$get$_$hgt()$
for(int i = 1; i <= len; i++) { if(rk[i] == 1) continue; int j = sa[rk[i-1]]; int k = max(1, hgt[rk[i-1]]-1); while(s[i+k-1] == s[j+k-1]) hgt[rk[i]] = k++; }
这里很简单qwq
重复一遍,hgt[]表示rk[]为i和i-1的后缀的LCP(最长公共前缀)长度。
显然,排名第一的前面没东西,即hgt[rk[1]] = 0。
暴力枚举?
设i为后缀序号,有这样一个定理:$hgt[rk[i]] ≥ hgt[rk[i-1]] - 1$
也就是第i位的hgt至少是第i-1位的hgt-1。
感性理解,举个例子:
s[] = aaaabbaa;
后缀有
aaaabbaa
aaabbaa
aabbaa
abbaa
bbaa
baa
aa
a排序之后有
a
aa
aaaabbaa
aaabbaa
aabbaa
abbaa
baa
bbaa它们对应的hgt(hgt[rk[]])01232101;
可以分成两种情况:i-1位的hgt=0,或hgt≠0。
为0时,显然hgt不可能为负;
不为0时,以i=3为例:hgt[rk[2]]=3,扣掉一位后,3-1=2。
这2位已经用来和hgt[rk[1]]匹配过了,所以可以直接跳过。
那么,枚举1~len后缀序号。
如果当前的后缀排名rk[i]为1,那它的hgt为0,直接跳过;
设j为排名为rk[i]-1,也就是排在i前的那个后缀的编号sa[rk[i]-1];
设k为相同的位数。由上述定理得,k = max(1, hgt[rk[i-1]]-1);
那么,跳过前k位,剩下的暴力枚举
分别从第i,j,位开始,如果第i+k-1和j+k-1的字符相同,则hgt[rk[i]] = k,k++;否则退出循环。
写了四个小时$QAQ$
模板题:Luogu P3809 【模板】后缀排序 (这个不用height)
完整代码如下

#include<cstdio> #include<iostream> #include<cmath> #include<cstring> #define MogeKo qwq #include<queue> using namespace std; const int maxn = 1e6+10; int buck[maxn]; int sa[maxn]; int trk[maxn]; int rk[maxn]; int hgt[maxn]; char s[maxn]; int len,cnt; bool Ssame(int a,int b,int k) { if(a+k > len || b+k > len) return false; return (rk[a] == rk[b]) && (rk[a+k] == rk[b+k]); } void get_sa() { for(int i = 1; i <= len; i++) buck[s[i]]++; for(int i = 0; i <= 122; i++) if(buck[i]) trk[i] = ++cnt; for(int i = 1; i <= 122; i++) buck[i] += buck[i-1]; for(int i = 1; i <= len; i++) { rk[i] = trk[s[i]]; sa[buck[s[i]]--] = i; } for(int k = 1; cnt != len; k <<= 1) { cnt = 0; for(int i = 0; i <= len; i++) buck[i] = 0; for(int i = 1; i <= len; i++) buck[rk[i]]++; for(int i = 1; i <= len; i++) buck[i] += buck[i-1]; for(int i = len; i; i--) if(sa[i] > k) trk[sa[i]-k] = buck[rk[sa[i]-k]]--; for(int i = len; i >= len-k+1; i--) trk[i] = buck[rk[i]]--; for(int i = 1; i <= len; i++) sa[trk[i]] = i; for(int i = 1; i <= len; i++) trk[sa[i]] = Ssame(sa[i],sa[i-1],k) ? cnt : ++cnt; for(int i = 1; i <= len; i++) rk[i] = trk[i]; } } void get_hgt() { for(int i = 1; i <= len; i++) { if(rk[i] == 1) continue; int j = sa[rk[i-1]]; int k = max(1, hgt[rk[i-1]]-1); while(s[i+k-1] == s[j+k-1]) hgt[rk[i]] = k++; } } int main() { scanf("%s",s+1); len = strlen(s+1); get_sa(); get_hgt(); for(int i = 1; i <= len; i++) printf("%d ",sa[i]); return 0; }
标签:ef6 公共前缀 不用 依次 回顾 计数排序 cat print 怎么
原文地址:https://www.cnblogs.com/mogeko/p/11324997.html