标签:tar strlen names map target 问题 break 穷举 i+1
POJ - 2406
题意:
给出一个字符串,要把它写成(x)n的形式,问n的最大值。
这题是求整个串的重复次数,不是重复最多次数的字串
这题很容易想到用KMP求最小循环节就没了,但是后缀数组也能写
后缀数组写法放在后面那一题,SPOJ - REPEATS是求子串类型,KMP就不好处理了
这里放下处理KMP的AC代码:

1 #include <cstdio> 2 #include <cstring> 3 #include <queue> 4 #include <cmath> 5 #include <algorithm> 6 #include <set> 7 #include <iostream> 8 #include <map> 9 #include <stack> 10 #include <string> 11 #include <time.h> 12 #include <vector> 13 #define pi acos(-1.0) 14 #define eps 1e-9 15 #define fi first 16 #define se second 17 #define rtl rt<<1 18 #define rtr rt<<1|1 19 #define bug printf("******\n") 20 #define mem(a,b) memset(a,b,sizeof(a)) 21 #define name2str(x) #x 22 #define fuck(x) cout<<#x" = "<<x<<endl 23 #define f(a) a*a 24 #define sf(n) scanf("%d", &n) 25 #define sff(a,b) scanf("%d %d", &a, &b) 26 #define sfff(a,b,c) scanf("%d %d %d", &a, &b, &c) 27 #define sffff(a,b,c,d) scanf("%d %d %d %d", &a, &b, &c, &d) 28 #define pf printf 29 #define FRE(i,a,b) for(i = a; i <= b; i++) 30 #define FREE(i,a,b) for(i = a; i >= b; i--) 31 #define FRL(i,a,b) for(i = a; i < b; i++)+ 32 #define FRLL(i,a,b) for(i = a; i > b; i--) 33 #define FIN freopen("data.txt","r",stdin) 34 #define gcd(a,b) __gcd(a,b) 35 #define lowbit(x) x&-x 36 #define rep(i,a,b) for(int i=a;i<b;++i) 37 #define per(i,a,b) for(int i=a-1;i>=b;--i) 38 39 using namespace std; 40 typedef long long LL; 41 typedef unsigned long long ULL; 42 const int maxn = 1e6 + 7; 43 const int maxm = 8e6 + 10; 44 const int INF = 0x3f3f3f3f; 45 const int mod = 10007; 46 47 char s[maxn]; 48 int n, nxt[maxn]; 49 void get_nxt() { 50 int j = -1, i = 0; 51 nxt[0] = -1; 52 while ( i < n ) { 53 if ( j == -1 || s[j] == s[i] ) nxt[++i] = ++j; 54 else j = nxt[j]; 55 } 56 } 57 int main() { 58 while ( scanf ( "%s", s ) && s[0] != ‘.‘ ) { 59 n = strlen ( s ); 60 get_nxt(); 61 if ( n % ( n - nxt[n] ) == 0 ) printf ( "%d\n", n / ( n - nxt[n] ) ); 62 else printf ( "1\n" ); 63 } 64 return 0; 65 }
SPOJ - REPEATS
题意:
求重复次数最多的连续重复子串
这个也是后缀数组求解的基本问题之一
"重复次数最多的连续重复子串"解法
(摘自罗穗骞的国家集训队论文):
先穷举长度L,然后求长度为L的子串最多能连续出现几次。
首先连续出现1次是肯定可以的,所以这里只考虑至少2次的情况。
假设在原字符串中连续出现2次,记这个子字符串为S,
那么S肯定包括了字符r[0], r[L], r[L*2],r[L*3], ……中的某相邻的两个。
所以只须看字符r[L*i]和r[L*(i+1)]往前和往后各能匹配到多远,
记这个总长度为K,那么这里连续出现了K/L+1次。最后看最大值是多少。如图所示。
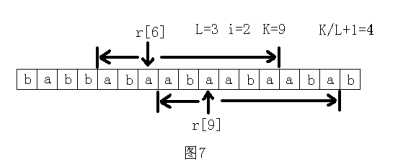
穷举长度 L 的时间是 n,每次计算的时间是 n/L。
所以整个做法的时间复杂 度是 O(n/1+n/2+n/3+……+n/n)=O(nlogn)。
如果读者看到这里还是有点迷,可以点击这里,这篇博客关于这题将的超级详细(而且我的后缀数组板子就是扒这个博主的)

1 #include <cstdio> 2 #include <cstring> 3 #include <queue> 4 #include <cmath> 5 #include <algorithm> 6 #include <set> 7 #include <iostream> 8 #include <map> 9 #include <stack> 10 #include <string> 11 #include <time.h> 12 #include <vector> 13 #define pi acos(-1.0) 14 #define eps 1e-9 15 #define fi first 16 #define se second 17 #define rtl rt<<1 18 #define rtr rt<<1|1 19 #define bug printf("******\n") 20 #define mem(a,b) memset(a,b,sizeof(a)) 21 #define name2str(x) #x 22 #define fuck(x) cout<<#x" = "<<x<<endl 23 #define f(a) a*a 24 #define sf(n) scanf("%d", &n) 25 #define sff(a,b) scanf("%d %d", &a, &b) 26 #define sfff(a,b,c) scanf("%d %d %d", &a, &b, &c) 27 #define sffff(a,b,c,d) scanf("%d %d %d %d", &a, &b, &c, &d) 28 #define pf printf 29 #define FRE(i,a,b) for(i = a; i <= b; i++) 30 #define FREE(i,a,b) for(i = a; i >= b; i--) 31 #define FRL(i,a,b) for(i = a; i < b; i++)+ 32 #define FRLL(i,a,b) for(i = a; i > b; i--) 33 #define FIN freopen("data.txt","r",stdin) 34 #define gcd(a,b) __gcd(a,b) 35 #define lowbit(x) x&-x 36 #define rep(i,a,b) for(int i=a;i<b;++i) 37 #define per(i,a,b) for(int i=a-1;i>=b;--i) 38 39 using namespace std; 40 typedef long long LL; 41 typedef unsigned long long ULL; 42 const int maxn = 1e6 + 7; 43 const int maxm = 8e6 + 10; 44 const int INF = 0x3f3f3f3f; 45 const int mod = 10007; 46 47 //rnk从0开始 48 //sa从1开始,因为最后一个字符(最小的)排在第0位 49 //height从1开始,因为表示的是sa[i - 1]和sa[i] 50 //倍增算法 O(nlogn) 51 int wa[maxn], wb[maxn], wv[maxn], ws_[maxn]; 52 int Rank[maxn], height[maxn], sa[maxn], r[maxn]; 53 int n, maxx; 54 char s[200]; 55 //Suffix函数的参数m代表字符串中字符的取值范围,是基数排序的一个参数,如果原序列都是字母可以直接取128,如果原序列本身都是整数的话,则m可以取比最大的整数大1的值 56 //待排序的字符串放在r数组中,从r[0]到r[n-1],长度为n 57 //为了方便比较大小,可以在字符串后面添加一个字符,这个字符没有在前面的字符中出现过,而且比前面的字符都要小 58 //同上,为了函数操作的方便,约定除r[n-1]外所有的r[i]都大于0,r[n-1]=0 59 //函数结束后,结果放在sa数组中,从sa[0]到sa[n-1] 60 void Suffix ( int *r, int *sa, int n, int m ) { 61 int i, j, k, *x = wa, *y = wb, *t; 62 //对长度为1的字符串排序 63 //一般来说,在字符串的题目中,r的最大值不会很大,所以这里使用了基数排序 64 //如果r的最大值很大,那么把这段代码改成快速排序 65 for ( i = 0; i < m; ++i ) ws_[i] = 0; 66 for ( i = 0; i < n; ++i ) ws_[x[i] = r[i]]++; //统计字符的个数 67 for ( i = 1; i < m; ++i ) ws_[i] += ws_[i - 1]; //统计不大于字符i的字符个数 68 for ( i = n - 1; i >= 0; --i ) sa[--ws_[x[i]]] = i; //计算字符排名 69 //基数排序 70 //x数组保存的值相当于是rank值 71 for ( j = 1, k = 1; k < n; j *= 2, m = k ) { 72 //j是当前字符串的长度,数组y保存的是对第二关键字排序的结果 73 //第二关键字排序 74 for ( k = 0, i = n - j; i < n; ++i ) y[k++] = i; //第二关键字为0的排在前面 75 for ( i = 0; i < n; ++i ) if ( sa[i] >= j ) y[k++] = sa[i] - j; //长度为j的子串sa[i]应该是长度为2 * j的子串sa[i] - j的后缀(第二关键字),对所有的长度为2 * j的子串根据第二关键字来排序 76 for ( i = 0; i < n; ++i ) wv[i] = x[y[i]]; //提取第一关键字 77 //按第一关键字排序 (原理同对长度为1的字符串排序) 78 for ( i = 0; i < m; ++i ) ws_[i] = 0; 79 for ( i = 0; i < n; ++i ) ws_[wv[i]]++; 80 for ( i = 1; i < m; ++i ) ws_[i] += ws_[i - 1]; 81 for ( i = n - 1; i >= 0; --i ) sa[--ws_[wv[i]]] = y[i]; //按第一关键字,计算出了长度为2 * j的子串排名情况 82 //此时数组x是长度为j的子串的排名情况,数组y仍是根据第二关键字排序后的结果 83 //计算长度为2 * j的子串的排名情况,保存到数组x 84 t = x; 85 x = y; 86 y = t; 87 for ( x[sa[0]] = 0, i = k = 1; i < n; ++i ) 88 x[sa[i]] = ( y[sa[i - 1]] == y[sa[i]] && y[sa[i - 1] + j] == y[sa[i] + j] ) ? k - 1 : k++; 89 //若长度为2 * j的子串sa[i]与sa[i - 1]完全相同,则他们有相同的排名 90 } 91 } 92 void calheight ( int *r, int *sa, int n ) { 93 int i, j, k = 0; 94 for ( i = 1; i <= n; i++ ) Rank[sa[i]] = i; 95 for ( i = 0; i < n; height[Rank[i++]] = k ) 96 for ( k ? k-- : 0, j = sa[Rank[i] - 1]; r[i + k] == r[j + k]; k++ ); 97 } 98 int minnum[maxn][16]; 99 void RMQ() { 100 int m = ( int ) ( log ( n * 1.0 ) / log ( 2.0 ) ); 101 for ( int i = 1 ; i <= n ; i++ ) minnum[i][0] = height[i]; 102 for ( int j = 1 ; j <= m ; j++ ) 103 for ( int i = 1 ; i + ( 1 << j ) - 1 <= n ; i++ ) 104 minnum[i][j] = min ( minnum[i][j - 1], minnum[i + ( 1 << ( j - 1 ) )][j - 1] ); 105 } 106 int query ( int a, int b ) { 107 int k = int ( log ( b - a + 1.0 ) / log ( 2.0 ) ); 108 return min ( minnum[a][k], minnum[b - ( 1 << k ) + 1][k] ); 109 } 110 int calprefix ( int a, int b ) { 111 int x = Rank[a], y = Rank[b]; 112 if ( x > y ) swap ( x, y ); 113 return query ( x + 1, y ); 114 } 115 int main() { 116 int T; 117 sf ( T ); 118 while ( T-- ) { 119 sf ( n ); 120 maxx = 0, r[n] = 0; 121 for ( int i = 0; i < n ; i++ ) { 122 scanf ( "%s", s ); 123 r[i] = ( int ) s[0], maxx = max ( maxx, r[i] ); 124 } 125 // for ( int i = 0 ; i < n ; i++ ) printf ( "%d%c", r[i], ( i == n - 1 ? ‘\n‘ : ‘ ‘ ) ); 126 Suffix ( r, sa, n + 1, maxx + 1 ); 127 calheight ( r, sa, n ); 128 RMQ(); 129 int ans = 0; 130 for ( int i = 1 ; i <= n ; i++ ) { 131 for ( int j = 0 ; j + i< n ; j += i ) { 132 int cnt = calprefix ( j, j+i ); 133 int temp = cnt / i + 1; 134 int k = j - ( i - cnt % i ); 135 if ( k >= 0 && calprefix ( k, k + i ) >= i ) temp++; 136 ans = max ( ans, temp ); 137 } 138 } 139 printf ( "%d\n", ans ); 140 } 141 return 0; 142 }
POJ - 3693:
题意:
要求输出重复次数最多的连续重复子串
若有多个连续重复子串的重复次数相同,输出字典序最小的一个
这题的类型和上一题的类型一样是求重复次数最多的连续重复子串
这题无非是多了一个输出字典序最小的方案而已。
我们在求解的过程中可以将所有方案数存下来,然后通过sa[ ]数组去进行枚举。
(因为sa数组就是通过字典序排序来的)(sa[i]表示字典序排名为i的起始下标)sa[0]表示空串。

1 #include <cstdio> 2 #include <cstring> 3 #include <queue> 4 #include <cmath> 5 #include <algorithm> 6 #include <set> 7 #include <iostream> 8 #include <map> 9 #include <stack> 10 #include <string> 11 #include <time.h> 12 #include <vector> 13 #define pi acos(-1.0) 14 #define eps 1e-9 15 #define fi first 16 #define se second 17 #define rtl rt<<1 18 #define rtr rt<<1|1 19 #define bug printf("******\n") 20 #define mem(a,b) memset(a,b,sizeof(a)) 21 #define name2str(x) #x 22 #define fuck(x) cout<<#x" = "<<x<<endl 23 #define f(a) a*a 24 #define sf(n) scanf("%d", &n) 25 #define sff(a,b) scanf("%d %d", &a, &b) 26 #define sfff(a,b,c) scanf("%d %d %d", &a, &b, &c) 27 #define sffff(a,b,c,d) scanf("%d %d %d %d", &a, &b, &c, &d) 28 #define pf printf 29 #define FRE(i,a,b) for(i = a; i <= b; i++) 30 #define FREE(i,a,b) for(i = a; i >= b; i--) 31 #define FRL(i,a,b) for(i = a; i < b; i++)+ 32 #define FRLL(i,a,b) for(i = a; i > b; i--) 33 #define FIN freopen("data.txt","r",stdin) 34 #define gcd(a,b) __gcd(a,b) 35 #define lowbit(x) x&-x 36 #define rep(i,a,b) for(int i=a;i<b;++i) 37 #define per(i,a,b) for(int i=a-1;i>=b;--i) 38 39 using namespace std; 40 typedef long long LL; 41 typedef unsigned long long ULL; 42 const int maxn = 1e6 + 7; 43 const int maxm = 8e6 + 10; 44 const int INF = 0x3f3f3f3f; 45 const int mod = 10007; 46 47 //rnk从0开始 48 //sa从1开始,因为最后一个字符(最小的)排在第0位 49 //height从1开始,因为表示的是sa[i - 1]和sa[i] 50 //倍增算法 O(nlogn) 51 int wa[maxn], wb[maxn], wv[maxn], ws_[maxn]; 52 int Rank[maxn], height[maxn], sa[maxn], r[maxn]; 53 int n, maxx; 54 char s[maxn]; 55 //Suffix函数的参数m代表字符串中字符的取值范围,是基数排序的一个参数,如果原序列都是字母可以直接取128,如果原序列本身都是整数的话,则m可以取比最大的整数大1的值 56 //待排序的字符串放在r数组中,从r[0]到r[n-1],长度为n 57 //为了方便比较大小,可以在字符串后面添加一个字符,这个字符没有在前面的字符中出现过,而且比前面的字符都要小 58 //同上,为了函数操作的方便,约定除r[n-1]外所有的r[i]都大于0,r[n-1]=0 59 //函数结束后,结果放在sa数组中,从sa[0]到sa[n-1] 60 void Suffix ( int *r, int *sa, int n, int m ) { 61 int i, j, k, *x = wa, *y = wb, *t; 62 //对长度为1的字符串排序 63 //一般来说,在字符串的题目中,r的最大值不会很大,所以这里使用了基数排序 64 //如果r的最大值很大,那么把这段代码改成快速排序 65 for ( i = 0; i < m; ++i ) ws_[i] = 0; 66 for ( i = 0; i < n; ++i ) ws_[x[i] = r[i]]++; //统计字符的个数 67 for ( i = 1; i < m; ++i ) ws_[i] += ws_[i - 1]; //统计不大于字符i的字符个数 68 for ( i = n - 1; i >= 0; --i ) sa[--ws_[x[i]]] = i; //计算字符排名 69 //基数排序 70 //x数组保存的值相当于是rank值 71 for ( j = 1, k = 1; k < n; j *= 2, m = k ) { 72 //j是当前字符串的长度,数组y保存的是对第二关键字排序的结果 73 //第二关键字排序 74 for ( k = 0, i = n - j; i < n; ++i ) y[k++] = i; //第二关键字为0的排在前面 75 for ( i = 0; i < n; ++i ) if ( sa[i] >= j ) y[k++] = sa[i] - j; //长度为j的子串sa[i]应该是长度为2 * j的子串sa[i] - j的后缀(第二关键字),对所有的长度为2 * j的子串根据第二关键字来排序 76 for ( i = 0; i < n; ++i ) wv[i] = x[y[i]]; //提取第一关键字 77 //按第一关键字排序 (原理同对长度为1的字符串排序) 78 for ( i = 0; i < m; ++i ) ws_[i] = 0; 79 for ( i = 0; i < n; ++i ) ws_[wv[i]]++; 80 for ( i = 1; i < m; ++i ) ws_[i] += ws_[i - 1]; 81 for ( i = n - 1; i >= 0; --i ) sa[--ws_[wv[i]]] = y[i]; //按第一关键字,计算出了长度为2 * j的子串排名情况 82 //此时数组x是长度为j的子串的排名情况,数组y仍是根据第二关键字排序后的结果 83 //计算长度为2 * j的子串的排名情况,保存到数组x 84 t = x; 85 x = y; 86 y = t; 87 for ( x[sa[0]] = 0, i = k = 1; i < n; ++i ) 88 x[sa[i]] = ( y[sa[i - 1]] == y[sa[i]] && y[sa[i - 1] + j] == y[sa[i] + j] ) ? k - 1 : k++; 89 //若长度为2 * j的子串sa[i]与sa[i - 1]完全相同,则他们有相同的排名 90 } 91 } 92 void calheight ( int *r, int *sa, int n ) { 93 int i, j, k = 0; 94 for ( i = 1; i <= n; i++ ) Rank[sa[i]] = i; 95 for ( i = 0; i < n; height[Rank[i++]] = k ) 96 for ( k ? k-- : 0, j = sa[Rank[i] - 1]; r[i + k] == r[j + k]; k++ ); 97 } 98 int minnum[maxn][17]; 99 void RMQ() { 100 int m = ( int ) ( log ( n * 1.0 ) / log ( 2.0 ) ); 101 for ( int i = 1 ; i <= n ; i++ ) minnum[i][0] = height[i]; 102 for ( int j = 1 ; j <= m ; j++ ) 103 for ( int i = 1 ; i + ( 1 << j ) - 1 <= n ; i++ ) 104 minnum[i][j] = min ( minnum[i][j - 1], minnum[i + ( 1 << ( j - 1 ) )][j - 1] ); 105 } 106 int query ( int a, int b ) { 107 int k = int ( log ( b - a + 1.0 ) / log ( 2.0 ) ); 108 return min ( minnum[a][k], minnum[b - ( 1 << k ) + 1][k] ); 109 } 110 int calprefix ( int a, int b ) { 111 int x = Rank[a], y = Rank[b]; 112 if ( x > y ) swap ( x, y ); 113 return query ( x + 1, y ); 114 } 115 int q[maxn]; 116 int main() { 117 int cas = 1; 118 while ( scanf ( "%s", s ) && s[0] != ‘#‘ ) { 119 n = strlen ( s ), r[n] = 0;; 120 maxx = 0; 121 for ( int i = 0; i < n ; i++ ) { 122 r[i] = ( int ) s[i], maxx = max ( maxx, r[i] ); 123 } 124 r[n] = 0; 125 // for ( int i = 0 ; i < n ; i++ ) printf ( "%d%c", r[i], ( i == n - 1 ? ‘\n‘ : ‘ ‘ ) ); 126 Suffix ( r, sa, n + 1, maxx + 1 ); 127 calheight ( r, sa, n ); 128 RMQ(); 129 int ans = 0, num = 0; 130 for ( int i = 1 ; i <= n ; i++ ) { 131 for ( int j = 0 ; j + i < n ; j += i ) { 132 int cnt = calprefix ( j, j + i ); 133 int temp = cnt / i + 1; 134 int k = j - ( i - cnt % i ); 135 if ( k >= 0 && calprefix ( k, k + i ) >= i ) temp++; 136 if ( ans == temp && i != q[num - 1] ) q[num++] = i; 137 else if ( ans < temp ) ans = temp, num = 0, q[num++] = i; 138 } 139 } 140 int flag = 0; 141 for ( int i = 1 ; i <= n ; i++ ) { 142 for ( int j = 0 ; j < num ; j++ ) { 143 if ( calprefix ( sa[i], sa[i] + q[j] ) >= q[j] * ( ans - 1 ) ) { 144 s[sa[i] + q[j]*ans] = ‘\0‘; 145 printf ( "Case %d: %s\n", cas++, s + sa[i] ); 146 flag = 1; 147 break; 148 } 149 } 150 if ( flag ) break; 151 } 152 } 153 return 0; 154 }
POJ - 2406 ~SPOJ - REPEATS~POJ - 3693 后缀数组求解重复字串问题
标签:tar strlen names map target 问题 break 穷举 i+1
原文地址:https://www.cnblogs.com/qldabiaoge/p/11329980.html