标签:分治策略 rate quick simple pivot ext util 维数 isp
1.快速排序(QuickSort)
1.1 快速排序是对冒泡排序的一种改进。通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另一部分的所有数据都要小,然后再按照此方法对这两部分数据进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
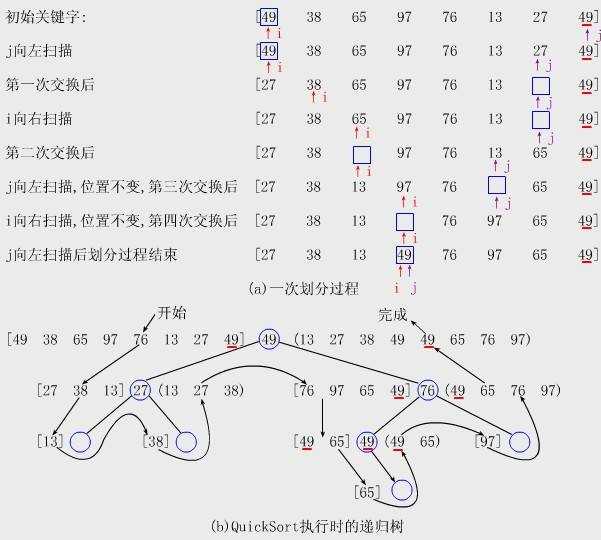
package cn.atguigu.sort; import java.text.SimpleDateFormat; import java.util.Arrays; import java.util.Date; public class QuickSort { public static void main(String[] args) { // TODO Auto-generated method stub // int[] arr= {-9,78,0,23,-567,70}; int[] arr = new int[80000]; for (int i = 0; i < arr.length; i++) { arr[i] = (int) (Math.random() * 8000); } Date date1 = new Date(); SimpleDateFormat simpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss"); String date1Str = simpleDateFormat.format(date1); System.out.println("排序前时间" + date1Str); quickSort(arr, 0, arr.length - 1); Date date2 = new Date(); String date2Str = simpleDateFormat.format(date2); System.out.println("排序后时间" + date2Str); // System.out.println(Arrays.toString(arr)); } public static void quickSort(int[] arr, int left, int right) { int l = left;// 左下标 int r = right;// 右下标 int pivot = arr[(left + right) / 2]; int temp = 0; // while循环的目的是让比pivot小的值放左边,大的值放右边 while (l < r) { // 在pivot的左边一直找,找到大于pivot的数 while (arr[l] < pivot) { l += 1; } // 在pivot的右边一直找,找到小于pivot的数 while (arr[r] > pivot) { r -= 1; } // 如果l>=r说明pivot的左右两的值,已将按照左边全部小于pivot值,右边全部大于pivot的值 if (l >= r) { break; } // 交换 temp = arr[l]; arr[l] = arr[r]; arr[r] = temp; // 交换完后,发现arr[l]==pivot,r--,前移 if (arr[l] == pivot) { r -= 1; } if (arr[r] == pivot) { l += 1; } } // 如果l==r,必须l++,r--,否则必须栈溢出 if (l == r) { l += 1; r -= 1; } // 向左递归 if (left < r) { quickSort(arr, left, r); } // 向右递归 if (right > l) { quickSort(arr, l, right); } } }
2.归并排序(MergeSort)
2.1 利用归并的思想实现排序,该算法采用经典的分治策略(divide-and-conquer)
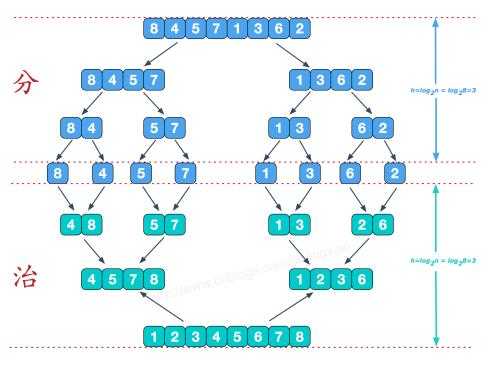
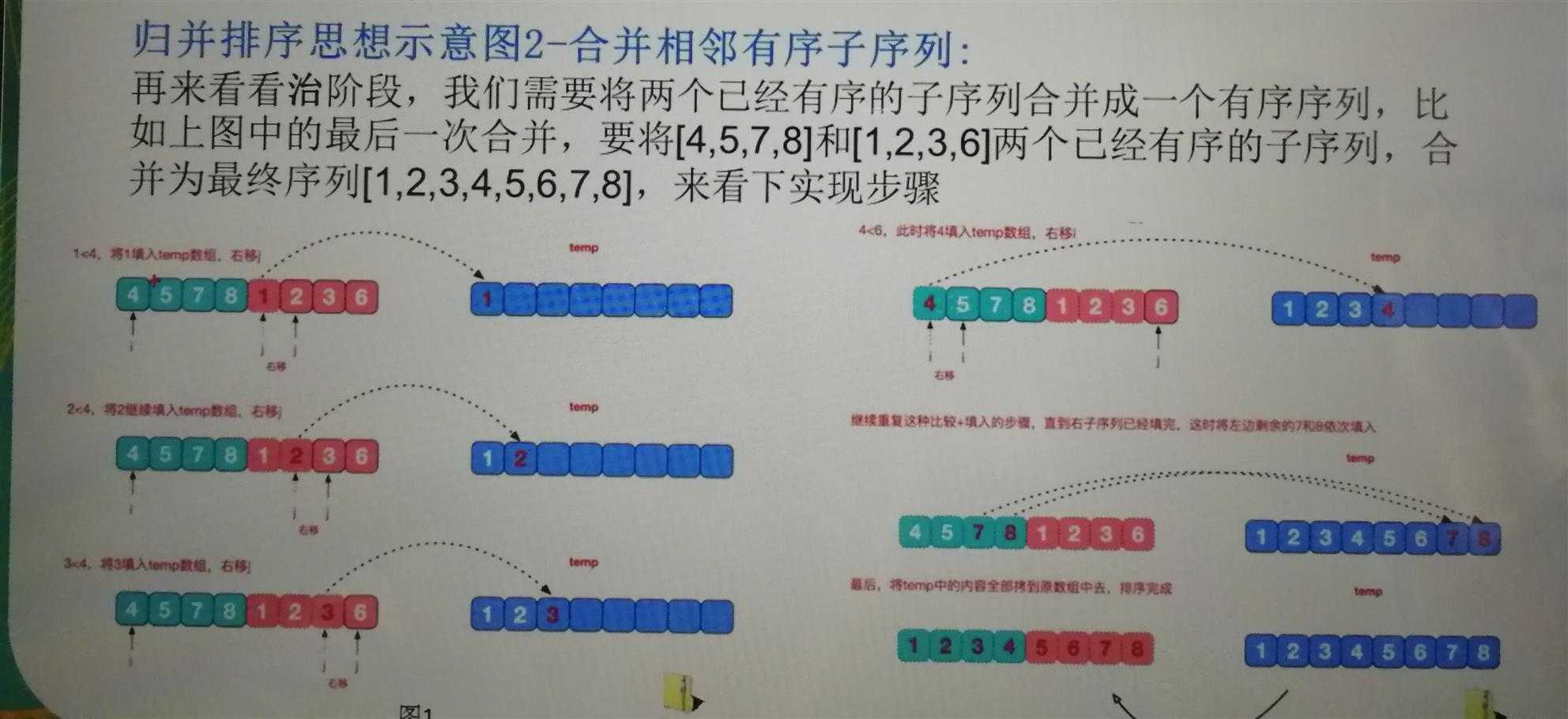
2.2 源代码
package cn.atguigu.sort; import java.text.SimpleDateFormat; import java.util.Arrays; import java.util.Date; public class MergeSort { public static void main(String[] args) { // int[] arr= {8,4,5,7,1,3,6,2}; int[] arr = new int[80000]; for (int i = 0; i < arr.length; i++) { arr[i] = (int) (Math.random() * 8000); } int temp[]=new int[arr.length];//归并排序需要额外的空间 Date date1 = new Date(); SimpleDateFormat simpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss"); String date1Str = simpleDateFormat.format(date1); System.out.println("排序前时间" + date1Str); mergeSort(arr, 0, arr.length-1, temp); Date date2 = new Date(); String date2Str = simpleDateFormat.format(date2); System.out.println("排序后时间" + date2Str); // System.out.println("归并排序后:"+Arrays.toString(arr)); } //分+合的方法 public static void mergeSort(int[] arr,int left,int right,int[] temp) { if(left<right) { int mid=(left+right)/2;//中间索引 //向左进行分解 mergeSort(arr, left, mid, temp); //向右进行分解 mergeSort(arr, mid+1, right, temp); //到合并 merge(arr, left, mid, right, temp); } } //合并的方法 /** * * @param arr 排序的数组 * @param left 左边有序序列的初始索引 * @param mid 中间索引 * @param right 右边索引 * @param temp 做中转的数组 */ public static void merge(int[] arr,int left,int mid,int right,int[]temp) { int i=left;//初始化i,左边有序序列的 初始索引 int j=mid+1;//初始化j,右边序列的初始索引 int t=0;//指向temp数组的当前索引 //先把左右两边的数据按照规则填充到temp数组,直到左右两边的有序序列有一方处理完毕 while(i<=mid&&j<=right) { if(arr[i]<=arr[j]) { temp[t]=arr[i]; i++; }else { temp[t]=arr[j]; j++; } t++; } //将剩余数据的一方的数据一次全部填充到temp while (i <= mid) { temp[t] = arr[i]; t++; i++; } while (j <= right) { temp[t] = arr[j]; t++; j++; } //将temp数组的元素全部拷贝到arr t=0; int tempLeft=left; while(tempLeft<=right) { arr[tempLeft]=temp[t]; t++; tempLeft++; } } }
3.基数排序又叫桶排序(radixSort)
3.1 属于分配式排序(distribution sort),通过键值的各个位的值,将要排序的元素分配至某些“桶”中,达到排序的作用,算法属于稳定性的排序,基数排序法是效率高的稳定性排序法
基数排序是桶排序的扩展,将整数按位数切割成不同的数字,然后每个位数分别比较。
3.2 将所有带比较数值统一为同样的数位长度,数位较短的数前面补0。然后,从最低位开始,依次进行一次排序。这样从最低位排序一直到最高位排序完成以后,数列就变成一个有序序列。
第1轮排序:
(1)将每个元素的个位数取出,然后看这个数应该放在哪个对应的桶(一个一维数组)
(2)按照这个桶的顺序(一维数组的下标依次取出数据,放入原来数组)
第2轮排序:
(1)将每个元素的十位数取出,然后看这个数应该放在哪个对应的桶(一个一维数组)
(2)按照这个桶的顺序(一维数组的下标依次取出数据,放入原来数组)
第3轮排序:
(1)将每个元素的百位数取出,然后看这个数应该放在哪个对应的桶(一个一维数组)
(2)按照这个桶的顺序(一维数组的下标依次取出数据,放入原来数组)
3.3 源代码
package cn.atguigu.sort; import java.text.SimpleDateFormat; import java.util.Arrays; import java.util.Date; public class radixSort { public static void main(String[] args) { // TODO Auto-generated method stub // int[] arr= {53,3,542,748,14,214}; int[] arr = new int[80000]; for (int i = 0; i < arr.length; i++) { arr[i] = (int) (Math.random() * 80000); } int temp[]=new int[arr.length];//归并排序需要额外的空间 Date date1 = new Date(); SimpleDateFormat simpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss"); String date1Str = simpleDateFormat.format(date1); System.out.println("排序前时间" + date1Str); radixSort(arr); Date date2 = new Date(); String date2Str = simpleDateFormat.format(date2); System.out.println("排序后时间" + date2Str); } public static void radixSort(int[] arr) { //最终代码 //1.得到数组中的最大的数的位数 int max=arr[0];//假设第一个数就是最大数 for(int i=0;i<arr.length;i++) { if(arr[i]>max) { max=arr[i]; } } //得到最大数是几位数 int maxLength=(max+"").length(); //使用循环代码处理 //定义一个二维数组,表示10个桶,每个桶就是一个一维数组 //说明 //1.二维数组包含10个一维数组 //2.为了防止在放入数的时候,数据溢出,则每一个一维数组,大小定位arr.length //3.明确基数排序是使用空间换时间的经典算法 int[][] bucket=new int[10][arr.length]; //为了记录每个桶中,实际存放了多少个数据,我们定义一个一维数组记录各个桶的每次放入的数据个数 //可以这样理解 //比如:bucketElementCounts[0],记录的就是bucket[0]桶的放入数据 int[] bucketElementCounts=new int[10]; for(int i=0,n=1;i<maxLength;i++,n*=10) { for (int j = 0; j < arr.length; j++) { //取出每个元素的个数 int digitOfElement=arr[j]/n%10; //放入到对应的桶中 bucket[digitOfElement][bucketElementCounts[digitOfElement]]=arr[j]; bucketElementCounts[digitOfElement]++; } //按照这个桶的顺序(一维数组的下标依次取出数据,放入原来数组) int index=0; //遍历每一个桶,并将桶中的数据,放入到原来的数组 for(int k=0;k<bucketElementCounts.length;k++) { //如果桶中,有数据,我们才放入到数组 if(bucketElementCounts[k]!=0) { //循环该桶即第k个桶(第k个一维数组),放入 for(int l=0;l<bucketElementCounts[k];l++) { //取出元素放入到arr arr[index]=bucket[k][l]; index++; } } //第i+1轮处理后,需要将每个bucketElementCounts[k]置0 bucketElementCounts[k]=0; } // System.out.println("第"+i+"轮,对个位的排序"+Arrays.toString(arr)); } } }
4.排序算法时间复杂度比较
4.1 相关术语解释:
(1)稳定:如果a原本在b前面,而a=b,排序后a仍然在b的前面;
(2)不稳定:如果a原本在b的前面,而a=b,排序之后a可能会出现在b的后面;
(3)内排序:所有排序操作都在内存中完成;
(4)外排序:由于数据太大,因此把数据放在磁盘中,而排序通过磁盘和内存的数据传输才能进行;
(5)时间复杂度:一个算法执行所耗费的时间;
(6)空间复杂度:运行完一个程序所需要内存的大小;
(7)n:数据规模
(8)k:“桶”的个数
(9)In-space:不占用额外内存
(10)Out-space:占用额外内存
4.2 常用算法对比
| 排序算法 | 平均时间复杂度 | 最好情况 | 最坏情况 | 空间复杂度 | 排序方式 | 稳定性 |
| 冒泡排序 | O(n2) | O(n) | O(n2) | O(1) | In-space | 稳定 |
| 选择排序 | O(n2) | O(n2) | O(n2) | O(1) | In-space | 不稳定 |
| 插入排序 | O(n2) | O(n) | O(n2) | O(1) | In-space | 稳定 |
| 希尔排序 | O(n log n) | O(n log2 n) | O(n log2 n) | O(1) | In-space | 不稳定 |
| 归并排序 | O(n log n) | O(n log n) | O(n log n) | O(n) | Out-space | 稳定 |
| 快速排序 | O(n log n) | O(n log n) | O(n2) | O(log n) | In-space | 不稳定 |
| 堆排序 | O(n log n) | O(n log n) | O(n log n) | O(1) | In-space | 不稳定 |
| 计数排序 | O(n+k) | O(n+k) | O(n+k) | O(k) | Out-space | 稳定 |
| 桶排序 | O(n+k) | O(n+k) | O(n2) | O(n+k) | Out-space | 稳定 |
| 基数排序 | O(n*k) | O(n*k) | O(n*k) | O(n+k) | Out-space | 稳定 |
标签:分治策略 rate quick simple pivot ext util 维数 isp
原文地址:https://www.cnblogs.com/ERFishing/p/11328760.html