标签:ret 创建 out 其它 最大 int 记录 范围 ati
基数排序(radix sort)属于“分配式排序”(distribution sort),又称“桶子法”(bucket sort)或bin sort,顾名思义,它是透过键值的部份资讯,将要排序的元素分配至某些“桶”中,藉以达到排序的作用,基数排序法是属于稳定性的排序,其时间复杂度为O (nlog(r)m),其中r为所采取的基数,而m为堆数,在某些时候,基数排序法的效率高于其它的稳定性排序法。
步骤:
一,求出一个数组中最大的数的位数,表示要排序多少次;
二,先根据个位数排序,个位数相同的放入相同的桶子中,分别对应着0-9的桶子;
三,然后将桶子中的数据重新串连起来,按照0-9的桶子顺序和先进先出的规则;
四,重复第二步和第三步,只是之后的个位数分别设为十位数,百位数,千位数......,直到排序次数完结。
执行过程图:
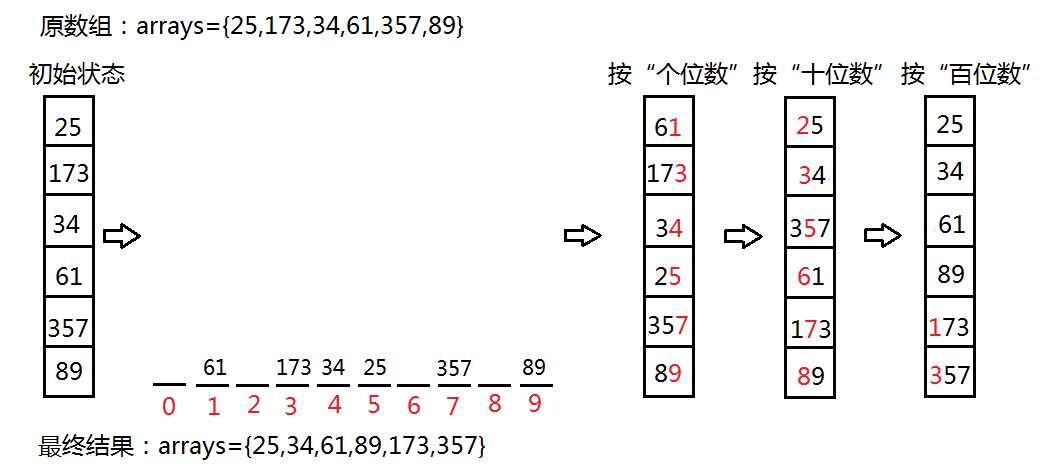
代码:
1 public class RadixSort { 2 //最大数的位数 3 public static int maxLength(int[] arrays){ 4 int maxArr = arrays[0]; 5 for (int i = 0; i < arrays.length-1; i++){ 6 if (arrays[i] < arrays[i+1]){ 7 maxArr = arrays[i+1]; 8 } 9 } 10 return (maxArr+"").length(); 11 } 12 //排序 13 public static void radix(int[] arrays){ 14 int i = 0; 15 int j; 16 int n = 1; 17 int index = 0; //数组下标 18 int l = arrays.length; //数组长度 19 int max = maxLength(arrays); //最大数的位数 20 //创建十个桶子数组 21 int[][] tempArr = new int[10][l]; 22 //每个桶子的定义 23 int[] counts = new int[10]; 24 while (i <= max){ 25 //把arrays数组中的数据分配到每个数组中 26 for (j = 0; j < l; j++){ 27 int temp = arrays[j]/n%10; 28 tempArr[temp][counts[temp]] = arrays[j]; 29 counts[temp]++; 30 } 31 //将每个桶子数组中的数据收集到arrays数组中 32 for (j = 0; j < counts.length; j++){ 33 for (int a = 0; a < counts[j]; a++){ 34 arrays[index] = tempArr[j][a]; 35 index++; 36 } 37 counts[j] = 0; 38 } 39 index = 0; 40 n = n*10; 41 i++; 42 } 43 } 44 //测试 45 public static void main(String[] args) { 46 int[] arrays={49,38,65,97,176,213,227,49,78,34,12,164,11,18,1}; 47 radix(arrays); 48 System.out.println(Arrays.toString(arrays)); 49 } 50 }
测试结果:
[1, 11, 12, 18, 34, 38, 49, 49, 65, 78, 97, 164, 176, 213, 227]
时间复杂度:设待排序列为n个记录,d为最大数的位数,radix为每个位数的取值范围。每次根据位数排序时,都会分为一趟收集和一趟分配,这个时间复杂度为O(n+radix);所以时间复杂度为O(d(n+radix))。
结语:优缺点还是不知道;
标签:ret 创建 out 其它 最大 int 记录 范围 ati
原文地址:https://www.cnblogs.com/mtgh/p/11368112.html