sklearn调用SVM算法

标签：直接   code   otl   proc   color   on()   shape   默认   图片   

1、支撑向量机SVM是一种非常重要和广泛的机器学习算法，它的算法出发点是尽可能找到最优的决策边界，使得模型的泛化能力尽可能地好，因此SVM对未来数据的预测也是更加准确的。

2、SVM既可以解决分类问题，又可以解决回归问题，原理整体相似，不过也稍有不同。

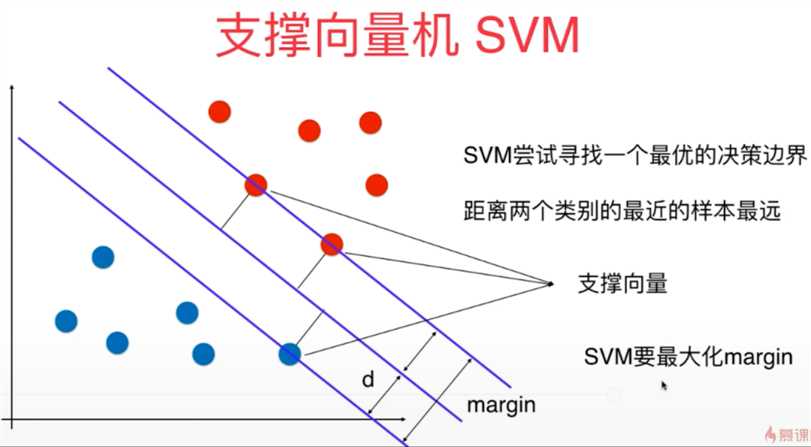
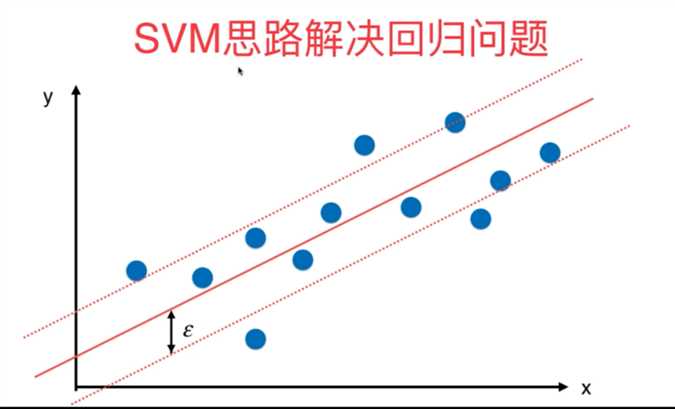
在sklearn章调用SVM算法的代码实现如下所示：

#（一）sklearn中利用SVM算法解决分类问题

import numpy as np
import matplotlib.pyplot as plt
from sklearn import  datasets
d=datasets.load_iris()
x=d.data
y=d.target
x=x[y<2,:2]
y=y[y<2]
print(x)
print(y)
plt.figure()
plt.scatter(x[y==0,0],x[y==0,1],color="r")
plt.scatter(x[y==1,0],x[y==1,1],color="g")
plt.show()
#进行数据据标准化处理（线性方式）
from sklearn.preprocessing import StandardScaler
s1=StandardScaler()
s1.fit(x)
x_standard=s1.transform(x)
print(np.hstack([x,x_standard]))
#导入sklearn中SVM的线性分类算法LinearSVC
from sklearn.svm import LinearSVC
s11=LinearSVC(C=1e9) #多分类问题的实现需要提交参数penalty=l1/l2（正则化方式）以及multi_class=ovo/ovr（采用何种方式多分类训练）
s11.fit(x_standard,y)
def plot_decision_boundary(model,axis):
    x0,x1=np.meshgrid(
        np.linspace(axis[0],axis[1],int((axis[1]-axis[0])*100)).reshape(-1,1),
        np.linspace(axis[2],axis[3], int((axis[3] - axis[2]) * 100)).reshape(-1,1)
    )
    x_new=np.c_[x0.ravel(),x1.ravel()]
    y_pre=model.predict(x_new)
    zz=y_pre.reshape(x0.shape)
    from matplotlib.colors import ListedColormap
    cus=ListedColormap(["#EF9A9A","#FFF59D","#90CAF9"])
    plt.contourf(x0,x1,zz,cmap=cus)
plot_decision_boundary(s11,axis=([-3,3,-3,3]))
plt.scatter(x_standard[y==0,0],x_standard[y==0,1],color="r")
plt.scatter(x_standard[y==1,0],x_standard[y==1,1],color="g")
plt.show()
print(s11.coef_)
print(s11.intercept_)
#输出svc函数的决策边界
def plot_svc_decision_boundary(model,axis):
    x0,x1=np.meshgrid(
        np.linspace(axis[0],axis[1],int((axis[1]-axis[0])*100)).reshape(-1,1),
        np.linspace(axis[2],axis[3], int((axis[3] - axis[2]) * 100)).reshape(-1,1)
    )
    x_new=np.c_[x0.ravel(),x1.ravel()]
    y_pre=model.predict(x_new)
    zz=y_pre.reshape(x0.shape)
    from matplotlib.colors import ListedColormap
    cus=ListedColormap(["#EF9A9A","#FFF59D","#90CAF9"])
    plt.contourf(x0,x1,zz,cmap=cus)
    w=model.coef_[0]
    b=model.intercept_[0]
    x1=np.linspace(axis[0],axis[1],200)
    upy=-w[0]*x1/w[1]-b/w[1]+1/w[1]
    downy=-w[0]*x1/w[1]-b/w[1]-1/w[1]
    upindex=((upy>axis[2])&(upy<axis[3]))
    downindex = ((downy > axis[2]) & (downy < axis[3]))
    plt.plot(x1[upindex],upy[upindex],"r")
    plt.plot(x1[downindex],downy[downindex],"g")
plot_svc_decision_boundary(s11,axis=([-3,3,-3,3]))
plt.scatter(x_standard[y==0,0],x_standard[y==0,1],color="r")
plt.scatter(x_standard[y==1,0],x_standard[y==1,1],color="g")
plt.show()

#sklearn中对于非线性数据的svm应用（多项式应用方式）
#1利用管道pipeline来进行多项式核函数的SVM算法
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
x,y=datasets.make_moons(noise=0.05,random_state=666)  #生成数据默认为100个数据样本
print(x.shape)
print(y.shape)
plt.figure()
plt.scatter(x[y==0,0],x[y==0,1],color="r")
plt.scatter(x[y==1,0],x[y==1,1],color="g")
plt.show()
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC
from sklearn.pipeline import Pipeline
def polyniomailSVC(degree,C=1.0):
    return Pipeline([("poly",PolynomialFeatures(degree=degree)),
                      ("std_scaler",StandardScaler()),
                      ("LinearSVC",LinearSVC(C=C))
                    ])

p=polyniomailSVC(degree=3)
p.fit(x,y)
plot_decision_boundary(p,axis=([-1,2.5,-1,1.5]))
plt.scatter(x[y==0,0],x[y==0,1],color="r")
plt.scatter(x[y==1,0],x[y==1,1],color="g")
plt.show()
#2直接利用sklearn中自带的多项式核函数SVM算法，主要的参数kernel="poly"
from sklearn.svm import SVC
def polynomialkernelSVC(degree,C=1.0):
    return Pipeline(
        [
            ("std_canler",StandardScaler()),
            ("kernelsvc",SVC(kernel="poly",degree=degree,C=C))
        ]
    )
p1=polynomialkernelSVC(degree=3)
p1.fit(x,y)
plot_decision_boundary(p1,axis=([-1,2.5,-1,1.5]))
plt.scatter(x[y==0,0],x[y==0,1],color="r")
plt.scatter(x[y==1,0],x[y==1,1],color="g")
plt.show()
#直观理解高斯核函数
import  numpy as np
import matplotlib.pyplot as plt
x=np.arange(-4,5,1)
y=np.array((x>=-2)&(x<=2),dtype="int")
print(x)
print(y)
plt.figure()
plt.scatter(x[y==0],[0]*len(x[y==0]),color="r")
plt.scatter(x[y==1],[0]*len(x[y==1]),color="g")
plt.show()
def gauss(x,y):
    gamma=1
    return np.exp(-gamma*(x-y)**2)
l1,l2=-1,1
x_new=np.empty((len(x),2))
for i ,data in enumerate(x):
    x_new[i,0]=gauss(data,l1)
    x_new[i,1]=gauss(data,l2)
plt.scatter(x_new[y==0,0],x_new[y==0,1],color="r")
plt.scatter(x_new[y==1,0],x_new[y==1,1],color="g")
plt.show()
#调用sklearn中的高斯核函数RBF核（超参数主要是gamma）
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
x,y=datasets.make_moons(noise=0.1,random_state=666)  #生成数据默认为100个数据样本
print(x.shape)
print(y.shape)
plt.figure()
plt.scatter(x[y==0,0],x[y==0,1],color="r")
plt.scatter(x[y==1,0],x[y==1,1],color="g")
plt.show()
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test=train_test_split(x,y,random_state=666)
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC
from sklearn.pipeline import Pipeline
def RBFkernelSVC(gamma):
    return Pipeline([
        ("std",StandardScaler()),
        ("svc",SVC(kernel="rbf",gamma=gamma))
    ])
sv=RBFkernelSVC(gamma=1)
sv.fit(x_train,y_train)
plot_decision_boundary(sv,axis=([-1.5,2.5,-1,1.5]))
plt.scatter(x[y==0,0],x[y==0,1],color="r")
plt.scatter(x[y==1,0],x[y==1,1],color="g")
plt.show()
print(sv.score(x_test,y_test))
from sklearn import datasets
d=datasets.load_iris()
x=d.data
y=d.target
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test=train_test_split(x,y,random_state=666)
sv=RBFkernelSVC(gamma=10)
sv.fit(x_train,y_train)
print(sv.score(x_test,y_test))

#（二）sklearn中利用SVM算法解决回归问题（epsilon为重要的超参数）
from sklearn import datasets
d=datasets.load_boston()
x=d.data
y=d.target
from sklearn.preprocessing import StandardScaler
s1=StandardScaler()
s1.fit(x)
x=s1.transform(x)
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test=train_test_split(x,y,random_state=666)
from sklearn.svm import LinearSVR
from sklearn.svm import SVR
from sklearn.preprocessing import StandardScaler
def StandardLinearSVR(epsilon):
    return Pipeline([
        ("std",StandardScaler()),
        ("svr",LinearSVR(epsilon=epsilon))
    ])
sv=LinearSVR()
param_grid=[{
    "epsilon":[i for i in np.arange(0,10,0.001)]
}]
from sklearn.model_selection import GridSearchCV
grid_search=GridSearchCV(sv,param_grid,n_jobs=-1,verbose=0)
grid_search.fit(x_train,y_train)
print(grid_search.best_params_)
print(grid_search.best_score_)
def polyniomailSVR(degree,C,epsilon):
    return Pipeline([("poly",PolynomialFeatures(degree=degree)),
                      ("std_scaler",StandardScaler()),
                      ("LinearSVC",LinearSVR(C=C,epsilon=epsilon))
                    ])
p1=polyniomailSVR(degree=2,C=1,epsilon=0.5)
p1.fit(x_train,y_train)
print(p1.score(x_test,y_test))

def polynomialkernelSVR(degree,coefo,epsilon):
    return Pipeline(
        [
            ("std_canler",StandardScaler()),
            ("kernelsvc",SVR(kernel="poly",degree=degree,coef0=coefo,epsilon=epsilon))
        ]
    )
p1=polynomialkernelSVR(degree=3,C=1,epsilon=0.1)
p1.fit(x_train,y_train)
print(p1.score(x_test,y_test))

def RBFkernelSVR(gamma,epsilon):
    return Pipeline([
        ("std",StandardScaler()),
        ("svc",SVR(kernel="rbf",gamma=gamma,epsilon=epsilon))
    ])
p2=RBFkernelSVR(gamma=0.05,epsilon=0.1)
p2.fit(x_train,y_train)
print(p2.score(x_test,y_test))

运行结果如下所示：

sklearn调用SVM算法

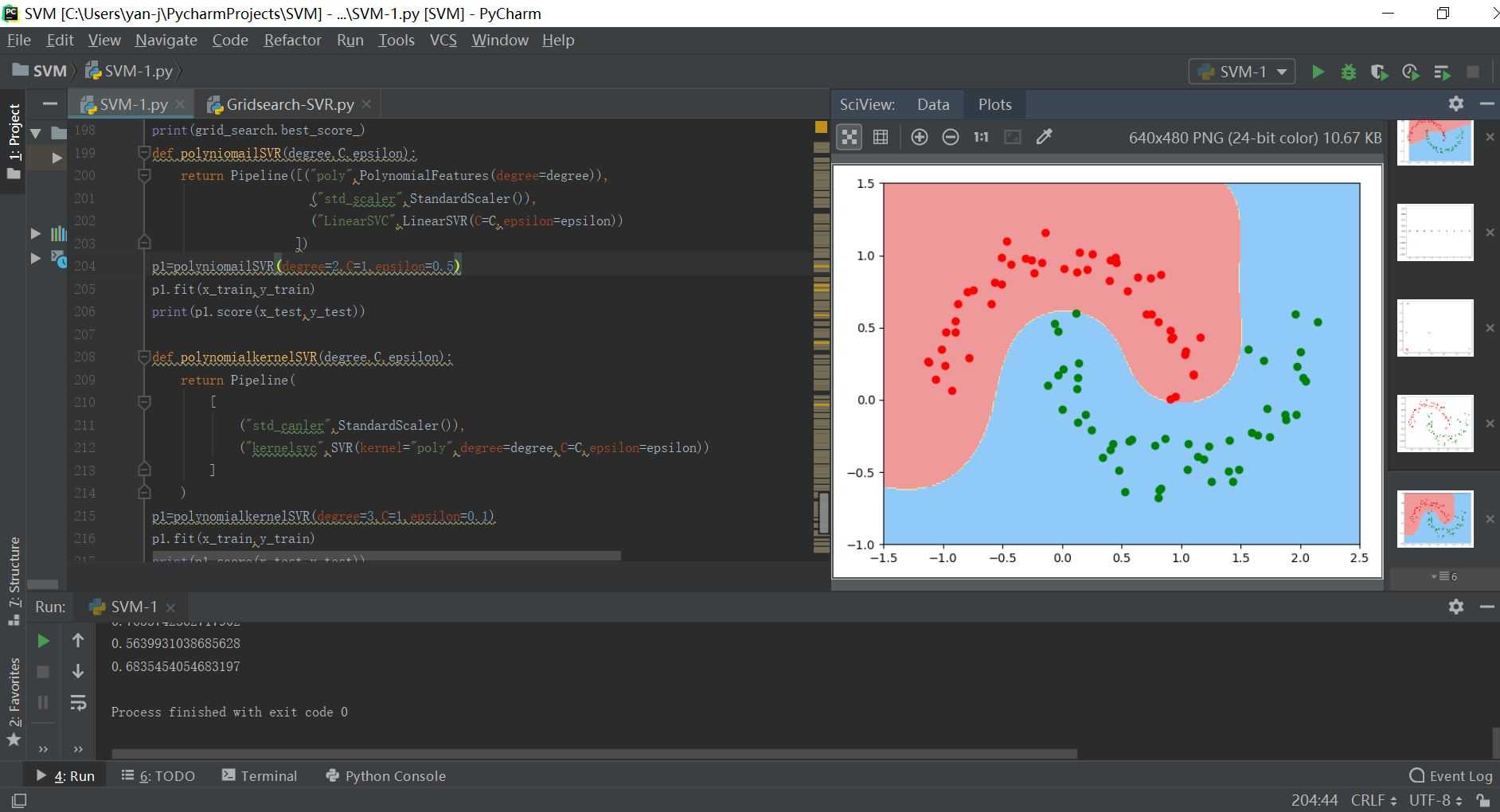
标签：直接   code   otl   proc   color   on()   shape   默认   图片   

原文地址：https://www.cnblogs.com/Yanjy-OnlyOne/p/11368253.html