标签:for ges 空间复杂度 技术 i++ pareto 相同 null 归并算法
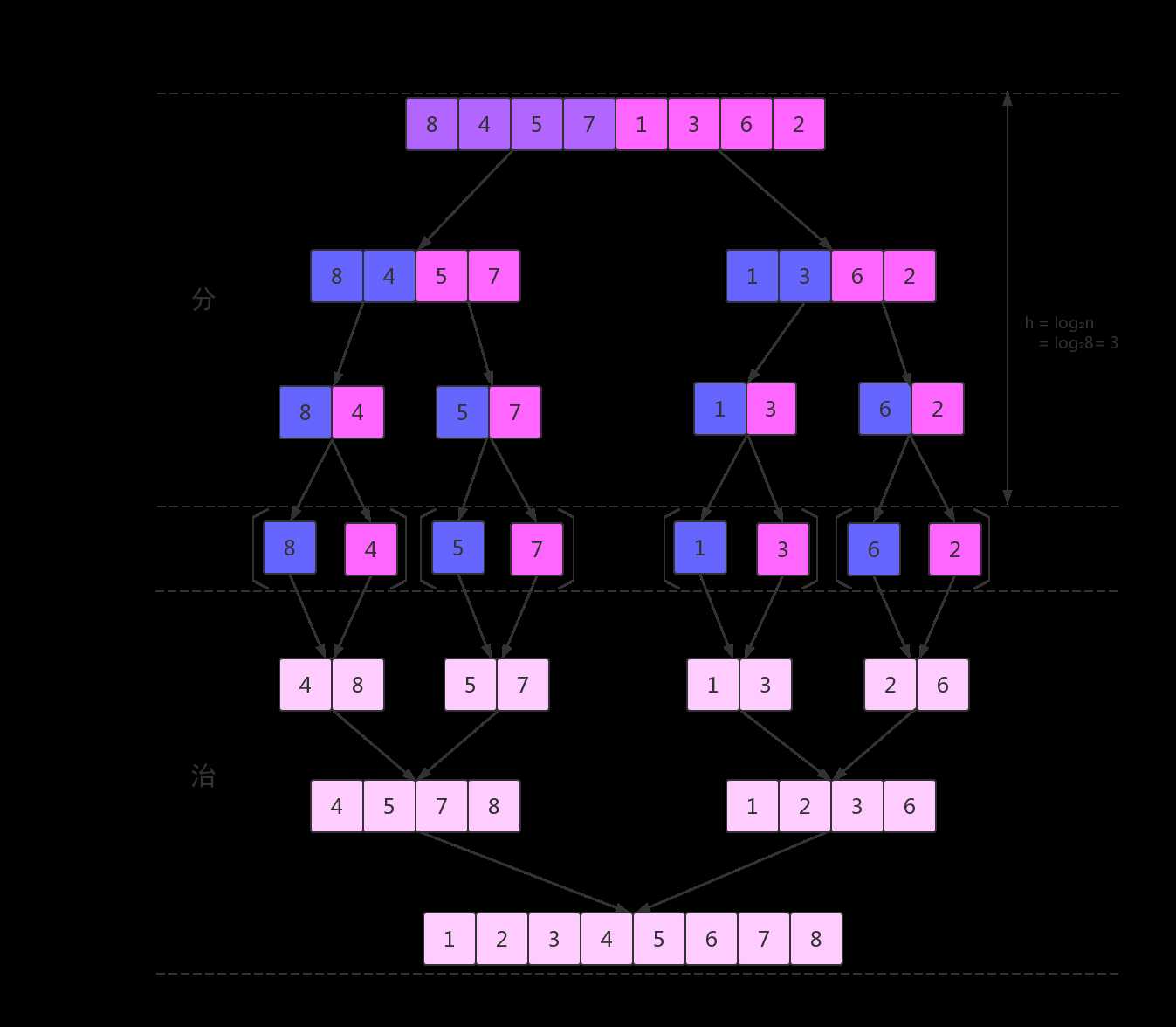
归并排序(英语:Merge sort,或mergesort),是创建在归并操作上的一种有效的排序算法,效率为O(n·log n)。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用,且各层分治递归可以同时进行。
采用分治法:
归并操作(merge),也叫归并算法,指的是将两个已经排序的序列合并成一个序列的操作。归并排序算法依赖归并操作。
归并排序代码如下:
1 static void merge_sort_recursive(int[] arr, int[] result, int start, int end) { 2 if(start>=end) 3 return; 4 int len = end - start, mid = (len >> 1) + start; //二进制位运算法`>>`,mid是指 5 int start1 = start, end1 = mid; 6 int start2 = mid + 1, end2 = end; 7 8 merge_sort_recursive(arr, result, start1, end1);//先拆左边 9 merge_sort_recursive(arr, result, start2, end2);//再拆右边 10 11 int k = start; 12 //拆完后治(排序),比较大小 13 while(start1 <= end1 && start2 <= end2) { 14 result[k++] = arr[start1] < arr[start2] ? arr[start1++]:arr[start2++]; 15 } 16 //合并 17 while(start1 <= end1) { 18 result[k++] = arr[start1++]; 19 } 20 while (start2 <= end2) { 21 result[k++] = arr[start2++]; 22 } 23 for(k = start;k <= end; k++) { 24 arr[k] = result[k]; 25 } 26 } 27 28 public static void merge_sort(int[] arr) { 29 int len = arr.length; 30 int[] result = new int[len]; 31 merge_sort_recursive(arr, result, 0, len - 1); 32 }
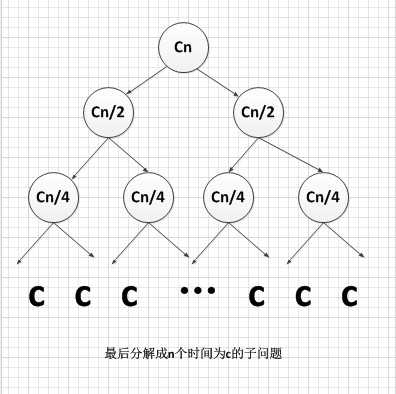
该算法使用了递归,思想是一直把数组分成两段,直至分成只有一个数,然后两段开始比较且开始合并,并复制到另外一个数组中。它的递归操作就像一个二叉树,处理完左边的子节点(?分的段)才开始处理右节点,处理右节点时也是先处理左节点,然后再处理右节点,就是这样一个过程。该算法额外占用了一个相同大小的空数组,因而空间复杂度为O(n)。从下面这个递归树可以看出,第一层时间代价为cn,第二层时间代价为cn/2+cn/2=cn.....每一层代价都是cn,总共有logn+1层,所以总的时间代价为cn*(logn+1),时间复杂度为O(n·logn)。
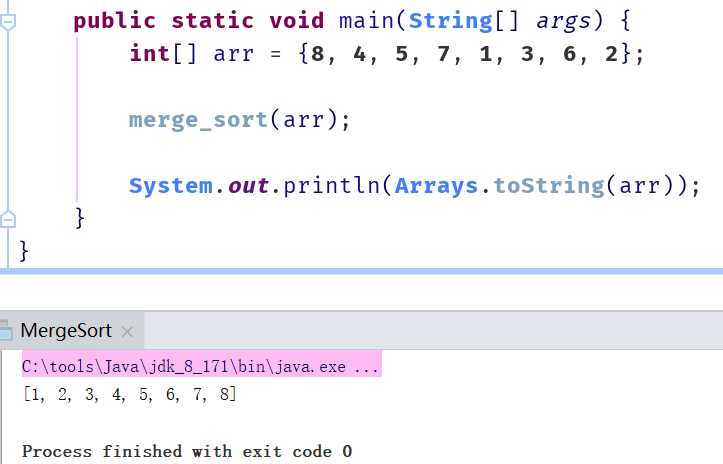
测试代码如下:
1 public static void main(String[] args) { 2 int[] arr = {8, 4, 5, 7, 1, 3, 6, 2}; 3 4 merge_sort(arr); 5 6 System.out.println(Arrays.toString(arr)); 7 }
结果如下:
JDK1.8中的归并排序
按照其元素的 Comparable 自然排序对指定的对象数组按升序排序。数组中的所有元素都必须实现 Comparable 接口。此外,数组中的所有元素必须是 相互比较(即 e1.compareTo(e2) )。
1 public static void sort(Object[] a) { 2 if (LegacyMergeSort.userRequested) 3 legacyMergeSort(a); 4 else 5 ComparableTimSort.sort(a, 0, a.length, null, 0, 0); 6 }
legacyMergeSort 用户请求传统的归并排序:
1 private static void legacyMergeSort(Object[] a) { 2 Object[] aux = a.clone(); 3 mergeSort(aux, a, 0, a.length, 0); 4 }
src是从索引0开始的源数组,dest是具有可能偏移量(可能更大的)目的数组,low是dest开始排序的位置索引,high是排序结束的最终位置索引,off是在src中相应的低、高的偏移量
1 @SuppressWarnings({"unchecked", "rawtypes"}) 2 private static void mergeSort(Object[] src, 3 Object[] dest, 4 int low, 5 int high, 6 int off) { 7 int length = high - low; 8 9 // 当小于这个值时使用插入排序由于合并排序 10 if (length < INSERTIONSORT_THRESHOLD) { 11 for (int i=low; i<high; i++) 12 for (int j=i; j>low && 13 ((Comparable) dest[j-1]).compareTo(dest[j])>0; j--) 14 swap(dest, j, j-1); 15 return; 16 } 17 18 // 递归地将dest的一半排序到src中 19 int destLow = low; 20 int destHigh = high; 21 low += off; 22 high += off; 23 int mid = (low + high) >>> 1; 24 mergeSort(dest, src, low, mid, -off); 25 mergeSort(dest, src, mid, high, -off); 26 27 // 优化,如果列表已经排序,则从src复制到dest中. 29 if (((Comparable)src[mid-1]).compareTo(src[mid]) <= 0) { 30 System.arraycopy(src, low, dest, destLow, length); 31 return; 32 } 33 34 // 将已排序的一半(现在在src中)合并到dest中 35 for(int i = destLow, p = low, q = mid; i < destHigh; i++) { 36 if (q >= high || p < mid && ((Comparable)src[p]).compareTo(src[q])<=0) 37 dest[i] = src[p++]; 38 else 39 dest[i] = src[q++]; 40 } 41 }
...
标签:for ges 空间复杂度 技术 i++ pareto 相同 null 归并算法
原文地址:https://www.cnblogs.com/magic-sea/p/11370186.html