标签:color clu lld ref 引入 传统 targe one style
树状数组:二进制的应用
与线段树的区别:树状数组的问题都可以用线段树解决,树状数组系数少,效率高
修改、查询复杂度 :O(log N)
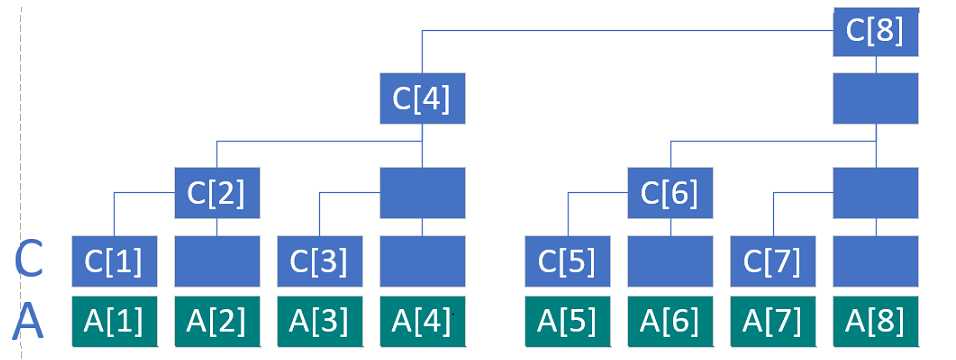
单点更新、区间查询:
C[1]=C[0001]=A[1]
C[2]=C[0010]=A[1]+A[2]
C[3]=C[0011]=A[3]
C[4]=C[0100]=A[1]+A[2]+A[3]+A[4]
C[5]=C[0101]=A[5]
C[6]=C[0110]=A[5]+A[6]
C[7]=C[0111]=A[7]
C[8]=C[1000]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8]
C[i]=A[i-2^k+1]+A[i-2^k+2]+...+A[i]
k:二进制中最低位到高位连续零的长度
Sum(i)=C[i]+C[i-2^k1]+C[(i-2^k1)-2^k2)+...
A[i] 包含于 C[i + 2k]、C[(i + 2k) + 2k]...
例如求前7项:C[7]+C[6]+C[4]
Sum[7]=sum[111]=C(100)+C(110)+C(111)
lowbit:取2^k
int lowbit(int x) { return x&(-x); }
更新函数
void updata(int x,int y) { for(int i=x;i<=n;i+=lowbit(i)) c[i]+=y; }
求和函数
int getsum(int x) { int ans=0; for(int i=x;i>0;i-=lowbit(i)) ans+=c[i]; return ans; }
例题:http://acm.hdu.edu.cn/showproblem.php?pid=1166

#include <bits/stdc++.h> using namespace std; int n,m; int a[50005],c[50005]; int lowbit(int x) { return x&(-x); } void updata(int x,int y) { for(int i=x;i<=n;i+=lowbit(i)) c[i]+=y; } int getsum(int x) { int ans=0; for(int i=x;i>0;i-=lowbit(i)) ans+=c[i]; return ans; } int main( ) { int t; cin>>t; int tot=1; while(t--) { cout << "Case " << tot++ << ":" << endl; memset(a, 0, sizeof a); memset(c, 0, sizeof c); cin>>n; for(int i = 1; i <= n; i++){ cin>>a[i]; updata(i,a[i]); } string s; int x,y; while(cin>>s && s[0] != ‘E‘) { cin>>x>>y; if(s[0] == ‘Q‘) { int sum = getsum(y) - getsum(x-1); cout << sum << endl; } else if(s[0] == ‘A‘) updata(x,y); else if(s[0] == ‘S‘) updata(x,-y); } } return 0; }
区间更新、单点查询:
把a-b区间内所有值全部加上k或者减去k
用传统树状数组复杂度不允许,不能再用数据的值建树
引入差分,利用差分建树
C[i]=a[i]-a[i-1] a为原数组
当某个区间[x,y]的值改变,区间内的差值不变
只有C[x]和C[y+1]的值改变了
对C[]数组建立树状数组
A[i]=Σ(i,j=1)C[i] 前面i项的差值和
例如:
A[0]=0;
A[]=1 2 3 5 6 9
C[]=1 1 1 2 1 3
把区间[3,5]加上2
A[]=1 2 5 7 8 9
C[]=1 1 3 2 1 1
C[3]的差值与C[5+1]的差值发生了改变
对C[]数组建立树状数组
例题:https://www.luogu.org/problem/P3368

#include <iostream> using namespace std; typedef long long ll; int a[500007],c[500007]; int n,m; int lowbit(int x) { return x&(-x); } void update(int x,int y) { for(int i=x;i<=n;i+=lowbit(i)) c[i]+=y; } int getsum(int x) { int ans=0; for(int i=x;i>0;i-=lowbit(i)) ans+=c[i]; return ans; } int main( ) { scanf("%d %d",&n,&m); a[0]=0; for(int i=1;i<=n;i++) { scanf("%d",&a[i]); update(i,a[i]-a[i-1]); } for(int i=1;i<=m;i++) { int flag,x,y; int k; scanf("%d",&flag); if(flag==1) { scanf("%d %d %d",&x,&y,&k); update(x,k); update(y+1,-k); } else { scanf("%d",&x); printf("%d\n",getsum(x)); } } return 0; }
区间更新、区间查询
还是利用差分
Σ(n,i=1)A[i]=Σ(n,i=1)Σ(i,j=1)D[j]
即:
A[1]+A[2]+...+A[n]
=(D[1])+(D[1]+D[2])+...+(D[1]+D[2]+..+D[n])
=n*D[1]+(n-1)*D[2]+...+D[n]
=n*(D[1]+D[2]+...+D[n])-(0*D[1]+1*D[2]+...+(n-1)*D[n])
所以: Σ(n,i=1)A[i]=n*Σ(n,i=1)D[i] - Σ(n,i=1)(D[i]*(i-1));
维护两个树状数组
A[i]=D[i]
B[i]=D[i]*(i-1);
例题:https://vjudge.net/problem/POJ-3468

#include <iostream> #include <cstdio> using namespace std; typedef long long ll; ll a[500007],c[500007]; ll A[500007],B[500007]; int n,m; int lowbit(int x) { return x&(-x); } void update(ll x,ll y) { ll k=x; for(int i=x;i<=n;i+=lowbit(i)) { A[i]+=y; B[i]+=y*(k-1); } } ll getsum(ll x) { ll ans=0; ll k=x; for(int i=x;i>0;i-=lowbit(i)) ans+=k*A[i]-B[i]; return ans; } int main( ) { scanf("%lld %lld",&n,&m); a[0]=0; for(int i=1;i<=n;i++) { scanf("%lld",&a[i]); update(i,a[i]-a[i-1]); } for(int i=1;i<=m;i++) { char s; cin>>s; ll x,y,k; if(s==‘Q‘) { scanf("%lld %lld",&x,&y); cout<<getsum(y)-getsum(x-1)<<endl; } else { scanf("%lld %lld %lld",&x,&y,&k); update(x,k); update(y+1,-k); } } return 0; }
树状数组还可以求逆序对、区间最大值,这些以后再更新了
标签:color clu lld ref 引入 传统 targe one style
原文地址:https://www.cnblogs.com/wronin/p/11372037.html