标签:递归 length 父节点 树的高度 添加节点 sel 删除节点 左右 lan
1.平衡二叉树基本介绍
1.1平衡二叉树又叫平衡二叉搜索树(Selg-balancing binary search tree),又叫AVL树,可以保证查询效率较高;
1.2 平衡二叉树是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是平衡二叉树。
1.3 平衡二叉树的常用实现方法有红黑树,AVL,替罪羊树,Treap,伸展树等;
2. AVL左旋转
2.1 左旋转流程(右子树的高度高)

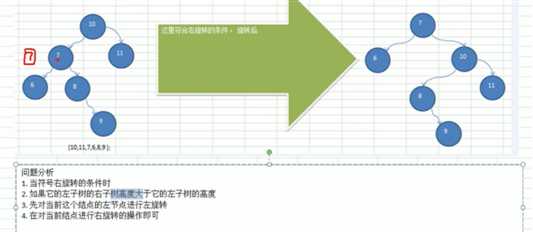
2.2 右旋转流程(左子树的高度高)

2.3 双旋转,存在以下的情况不能单单进行一方旋转
2.4 代码实现
1 package cn.atguigu.AVL; 2 3 4 public class AVLTreeDemo { 5 6 public static void main(String[] args) { 7 // int[] arr= {4,3,6,5,7,8}; 8 // int[] arr= {10,12,8,9,7,6}; 9 int[] arr= {10,11,7,6,8,9}; 10 //创建AVLTree对象 11 AVLTree avlTree=new AVLTree(); 12 //添加节点 13 for (int i = 0; i < arr.length; i++) { 14 avlTree.add(new Node(arr[i])); 15 } 16 17 //遍历 18 System.out.println("中序遍历"); 19 avlTree.infixOrder(); 20 21 System.out.println("做平衡处理"); 22 System.out.println("left树的高度="+avlTree.getRoot().leftHeight()); 23 System.out.println("right树的高度="+avlTree.getRoot().rightHeight()); 24 } 25 26 } 27 28 //创建AVL树 29 class AVLTree { 30 private Node root; 31 32 public Node getRoot() { 33 return root; 34 } 35 36 // 查找要删除的节点 37 public Node search(int value) { 38 if (root == null) { 39 return null; 40 } else { 41 return root.search(value); 42 } 43 } 44 45 // 查找要删除节点的父节点 46 public Node searchParent(int value) { 47 if (root == null) { 48 return root; 49 } else { 50 return root.searchParent(value); 51 } 52 } 53 54 /** 55 * 1.返回以node为根节点的二叉排序树的最小节点的值 2.删除以node为根节点的二叉排序树的最小节点的值 56 * 57 * @param node 传入的节点,当作二叉排序树的根节点 58 * @return 返回以node为根节点的二叉排序树的最小节点的值 59 */ 60 public int delRightTreeMin(Node node) { 61 Node target = node; 62 // 循环查找的左节点,会找到最小值 63 while (target.left != null) { 64 target = target.left; 65 } 66 // 这是target指向了最小节点 67 // 删除最小节点 68 delNode(target.value); 69 return target.value; 70 } 71 72 // 删除节点 73 public void delNode(int value) { 74 75 if (root == null) { 76 return; 77 } else { 78 // 找到要删除的节点targetNode; 79 Node targetNode = root.search(value); 80 if (targetNode == null) 81 return;// 如果没有找到该接待你 82 // 如果当前这颗二叉排序树只有一个节点 83 if (root.left == null && root.right == null) { 84 root = null; 85 return; 86 } 87 // 找到targetNode的父节点 88 Node parent = root.searchParent(value); 89 // 如果删除的节点是叶子节点 90 if (targetNode.left == null && targetNode.right == null) { 91 if (parent.left != null && parent.left.value == value) {// 判断targetNode是父节点的左子节点还是右子节点 92 parent.left = null; 93 } else if (parent.right != null && parent.right.value == value) {// 是右子节点 94 parent.right = null; 95 } 96 } else if (targetNode.left != null && targetNode.right != null) {// targetNode有左子树和右子树 97 int minVal = delRightTreeMin(targetNode.right); 98 targetNode.value = minVal; 99 } else {// 删除只有一颗子树的节点 100 // 如果要删除的节点有左子节点 101 if (targetNode.left != null) { 102 if (parent != null) { 103 if (parent.left.value == value) {// targetNode是parent的左子节点 104 parent.left = targetNode.left; 105 } else {// targetNode是parent的右子节点 106 parent.right = targetNode.left; 107 } 108 } else { 109 root = targetNode.left; 110 } 111 } else { 112 if (parent != null) { 113 // 如果要删除的节点有右子节点 114 if (parent.left.value == value) {// targetNode是parent的左子节点 115 parent.left = targetNode.right; 116 } else {// targetNode是parent的右子节点 117 parent.right = targetNode.right; 118 } 119 } else { 120 root = targetNode.right; 121 } 122 123 } 124 } 125 } 126 } 127 128 // 添加节点的方法 129 public void add(Node node) { 130 if (root == null) { 131 root = node;// 如果root为空,直接让root指向node 132 } else { 133 root.add(node); 134 } 135 } 136 137 // 重载 138 public void infixOrder() { 139 this.infixOrder(root); 140 } 141 142 // 中序遍历方法 143 public void infixOrder(Node root) { 144 if (root == null) { 145 System.out.println("树为空,无法遍历"); 146 } else { 147 root.infixOrder(); 148 } 149 } 150 } 151 //创建NOde节点 152 class Node { 153 int value; 154 Node left; 155 Node right; 156 public Node(int value) { 157 this.value = value; 158 } 159 //返回左子树的高度 160 public int leftHeight() { 161 if(left==null) { 162 return 0; 163 } 164 return left.height(); 165 } 166 //返回右子树的高度 167 public int rightHeight() { 168 if(right==null) { 169 return 0; 170 } 171 return right.height(); 172 } 173 //返回当前节点的高度,以该节点为树的高度 174 public int height() { 175 return Math.max(left==null? 0:left.height(), right==null? 0:right.height())+1; 176 } 177 178 @Override 179 public String toString() { 180 return "Node [value=" + value + "]"; 181 } 182 183 //右旋转 184 private void rightRotate() { 185 Node newNode=new Node(value); 186 newNode.right=right; 187 newNode.left=left.right; 188 value=left.value; 189 left=left.left; 190 right=newNode; 191 } 192 193 //左旋转方法 194 private void leftRotate() { 195 //创建新的节点,以当前根节点的值 196 Node newNode=new Node(value); 197 //把新的节点的左子树设置成当前节点的左子树 198 newNode.left=left; 199 //把新的节点的右子树设置成当前节点的右子树的左子树 200 newNode.right=right.left; 201 //把当前节点的值替换成右子树的值 202 newNode.value=right.value; 203 //把当前节点的右子树设置成当前节点的右子树的右子树 204 right=right.right; 205 //把当前节点的左子树设置成新的节点 206 left=newNode; 207 } 208 // 查找要删除的节点 209 /** 210 * 211 * @param value 希望删除的节点的值 212 * @return 找到返回,没有返回null 213 */ 214 public Node search(int value) { 215 if (value == this.value) { 216 return this; 217 } else if (value < this.value) {// 如果查找的值小于当前节点,向左子树递归查找 218 if (this.left == null) { 219 return null; 220 } 221 return this.left.search(value); 222 } else {// 如果查找的值不小于当前节点,向右子树递归查找 223 if (this.right == null) { 224 return null; 225 } 226 return this.right.search(value); 227 } 228 } 229 230 // 查找要删除节点的父节点 231 /** 232 * 233 * @param value 要找到的节点的值 234 * @return 找到返回的是要删除节点的父节点的值,否则返回null 235 */ 236 public Node searchParent(int value) { 237 // 如果当前节点是要删除节点的父节点,就返回 238 if ((this.left != null && this.left.value == value) || (this.right != null && this.right.value == value)) { 239 return this; 240 } else { 241 // 如果查找的值小于当前节点的值,并且当前节点的左子节点不为空 242 if (value < this.value && this.left != null) { 243 return this.left.searchParent(value);// 向左子树递归查找 244 } else if (value >= this.value && this.right != null) { 245 return this.right.searchParent(value);// 向右子树递归查找 246 } else { 247 return null;// 没有找到父节点 248 } 249 } 250 } 251 252 // 添加节点的方法 253 // 递归的形式添加节点,注意需要满足二叉排序树的要求 254 public void add(Node node) { 255 if (node == null) { 256 return; 257 } 258 // 判断传入的节点的值,和当前子树的根节点的值关系 259 if (node.value < this.value) { 260 // 如果当前节点的左子节点为null 261 if (this.left == null) { 262 this.left = node; 263 } else {// 递归向左子树添加 264 this.left.add(node); 265 } 266 } else { 267 // 如果当前节点的右子节点为null 268 if (this.right == null) { 269 this.right = node; 270 } else {// 递归向右子树添加 271 this.right.add(node); 272 } 273 } 274 //当添加完一个节点后,如果:右子树的高度-左子树的高度>1,左旋转 275 if(rightHeight()-leftHeight()>1) { 276 //如果它的右子树的左子树的高度大于它的右子树的高度 277 if(right!=null&&right.leftHeight()>right.rightHeight()) { 278 //先对右子节点进行右旋转 279 right.rightRotate(); 280 //再对当前节点进行左旋转 281 leftRotate(); 282 }else { 283 leftRotate(); 284 } 285 return;//必须要 286 } 287 //当添加完一个节点后,如果:左子树的高度-右子树的高度>1,右旋转 288 if(leftHeight()-rightHeight()>1) { 289 //如果它的左子树的右子树的高度大于它的左子树的高度 290 if(left!=null && left.rightHeight()>left.leftHeight()) { 291 //先对当前节点的左节点进行左旋转 292 left.leftRotate(); 293 //再对当前节点进行右旋转 294 rightRotate(); 295 }else { 296 rightRotate(); 297 } 298 } 299 } 300 301 // 中序遍历二叉树 302 public void infixOrder() { 303 if (this.left != null) { 304 this.left.infixOrder(); 305 } 306 System.out.println(this); 307 if (this.right != null) { 308 this.right.infixOrder(); 309 } 310 } 311 }
标签:递归 length 父节点 树的高度 添加节点 sel 删除节点 左右 lan
原文地址:https://www.cnblogs.com/ERFishing/p/11377523.html