标签：i++   package   tst   const   递归算法   lan   reac   count   range   

假设有一款不会反复清扫同一个地方的机器人，它只能前后左右移动。举个例子，如果第1次向后移动，那么连续移动3次时，就会有以下9种情况（图6）。又因为第1次移动可以是前后左右4种情况，所以移动3次时全部路径有9×4＝36种。

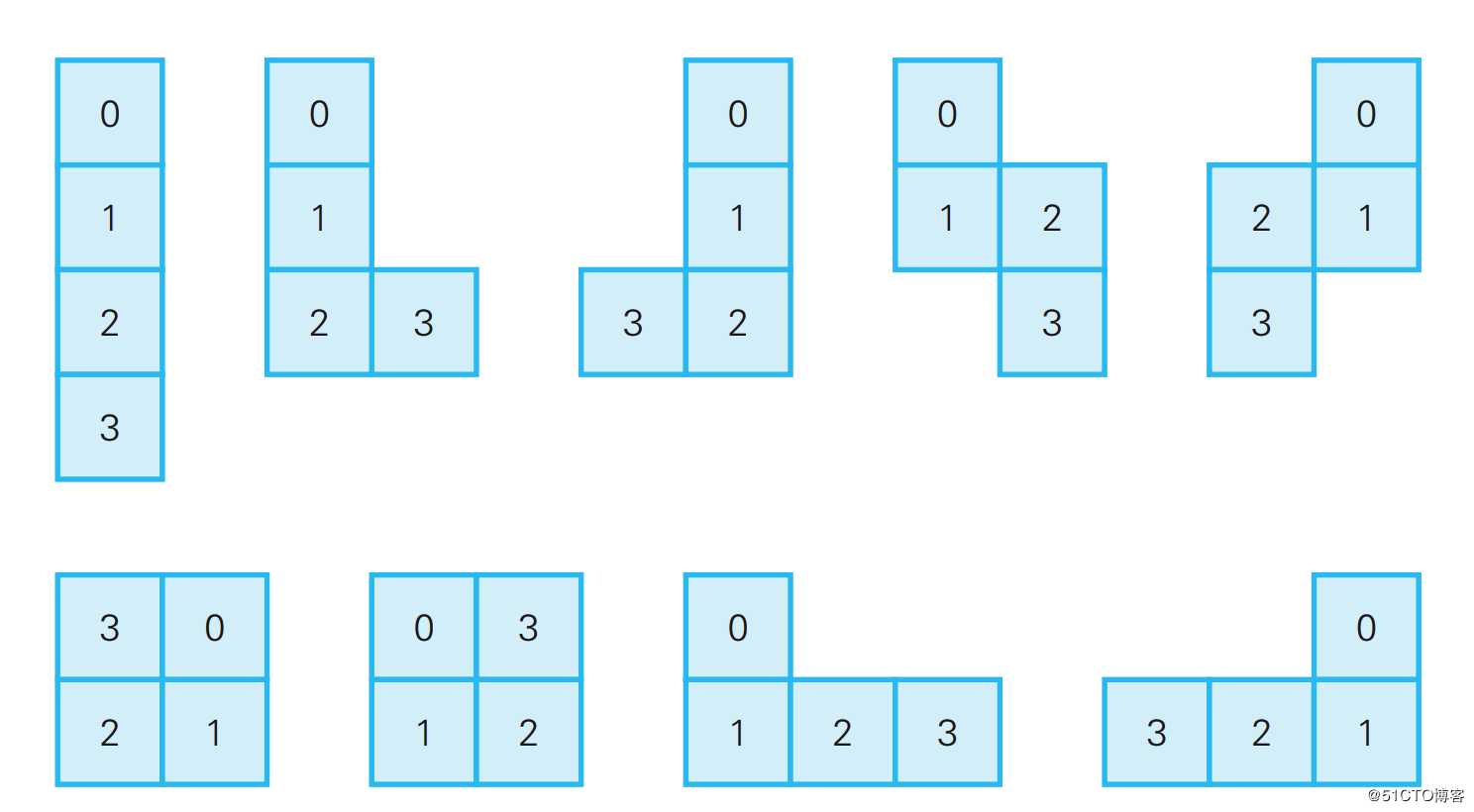
求这个机器人移动12次时，有多少种移动路径？

思路：

尝试用递归和非递归两种办法来解。

递归思路：
从起点开始，在各方向移动1步，如果移动后的点不在当前的路径中，就加入到当前路径中，并进行下一次移动，当移到到指定的N步时，退出，并计数加1，视为找到一条路径。

非递归思路：
1.从1开始逐一加大移动步数，直至达到N步。
2.将相同步数的路径视为同一批，将同一批的每一条路径依次POP出来。
3.找到每条路径的最后一个点，进行4个方向的移动，如果下一个点不在该路径中，视为一条新路径，并存放至临时表中。
4.待这一批所有的路径处理完后，将临时表赋值给全局路径记录表。

解答：

php:

ini_set(‘memory_limit‘,‘1024M‘);

class Machine
{
    const N = 12;
    private $directions = array(array(0, 1), array(0, -1), array(1, 0), array(-1, 0));
    private $stepList = array();

    // 移动 - 递归算法
    function move($log = array())
    {
        // 刚好走了N+1步，就结束本次递归，认为找到了一条路径
        if (count($log) == self::N + 1) {

            // 如果需要记录路径，请打开此注释
            //$this->stepList[] = $log;
            return 1;
        }

        $cnt = 0;
        $last = end($log);
        foreach ($this->directions as $d) {
            $nextPos = array($last[0] + $d[0], $last[1] + $d[1]);
            if (!in_array($nextPos, $log)) {
                $cnt += $this->move(array_merge($log, array($nextPos)));
            }
        }
        return $cnt;
    }

    // 如果递归方法中开启了路径记录注释，则可以用此方法取得所有的路径
    function getStepList()
    {
        return $this->stepList;
    }

    // 移动 - 非递归算法
    function move2($startPoint)
    {
        $allFootprint = array(array($startPoint));

        // 遍历步数
        for ($i = 0; $i < self::N; $i++) {
            $allNewFootprint = array();
            while (count($allFootprint) > 0) {

                // 消费前置数据，每次从最后取一条路径出来
                $curFootprint = array_pop($allFootprint);

                // 找到路径中的最后一个节点
                $last = end($curFootprint);

                // 各方向走一步
                foreach ($this->directions as $d) {
                    $nextPos = array($last[0] + $d[0], $last[1] + $d[1]);

                    // 没走过的点加入到新路径中
                    if (!in_array($nextPos, $curFootprint)) {
                        $allNewFootprint[] = array_merge($curFootprint, array($nextPos));
                    }
                }
            }
            $allFootprint = $allNewFootprint;// 保存本次结果，作为下一次处理的前置数据
        }
        return $allFootprint;
    }
}

$Machine = new Machine();
$rs = $Machine->move(array(array(0, 0)));
echo $rs."\n";
$rs = $Machine->move2(array(0, 0));
echo count($rs)."\n";

输出：

324932
324932

golang:

package main

import "fmt"

type Point struct {
    X int
    Y int
}

const N = 12

var directions = [][]int{{0, 1}, {0, -1}, {1, 0}, {-1, 0}}

func main() {
    p := Point{0, 0}
    rs := move([]Point{p})
    fmt.Println(rs)

    rs2 := move2(p)
    //for _, value := range rs2 {
    //    fmt.Println(value)
    //}
    fmt.Println(len(rs2))
}

func move(log []Point) int {
    logLength := len(log)
    if logLength == N+1 {
        return 1
    }

    cnt := 0
    last := log[logLength-1]
    for _, d := range directions {
        nextPos := Point{last.X + d[0], last.Y + d[1]}
        if !inArray(nextPos, log) {
            cnt += move(append(log, nextPos))
        }
    }
    return cnt
}

func move2(startPoint Point) [][]Point {
    allFootPrint := [][]Point{{startPoint}}
    for i := 0; i < N; i++ {
        allNewFootPrint := make([][]Point, 0)
        for len(allFootPrint) > 0 {
            // pop一条路径
            curFootPrint := allFootPrint[len(allFootPrint)-1]
            allFootPrint = allFootPrint[:len(allFootPrint)-1]
            last := curFootPrint[len(curFootPrint)-1]
            for _, d := range directions {
                nextPoint := Point{last.X + d[0], last.Y + d[1]}
                if !inArray(nextPoint, curFootPrint) {
                    // 必须复制一份数据出来，否则会发生路径重复
                    newCurFootPrint := make([]Point, len(curFootPrint))
                    copy(newCurFootPrint, curFootPrint)

                    allNewFootPrint = append(allNewFootPrint, append(newCurFootPrint, nextPoint))
                }
            }
        }
        allFootPrint = allNewFootPrint
    }
    return allFootPrint
}

// 检查某个点是否在路径中
func inArray(need Point, needArr []Point) bool {
    for _, v := range needArr {
        if need == v {
            return true
        }
    }
    return false
}

输出：

324932
324932

每周一道算法题010：扫地机器人路径统计

标签：i++   package   tst   const   递归算法   lan   reac   count   range   

原文地址：https://blog.51cto.com/ustb80/2431586