标签:并且 not adt info def first queue padding 广度优先搜索
回溯法(探索与回溯法)是一种选优搜索法,按选优条件向前搜索,以达到目标。
但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,
这种走不通就退回再走的技术为回溯法,而满足回溯条件的某个状态的点称为“回溯点”。
深度优先搜索的主要特征就是,假设一个顶点有不少相邻顶点,当我们搜索到该顶点,我们对于它的相邻顶点并不是现在就对所有都进行搜索,
而是对一个顶点继续往后搜索,直到某个顶点,他周围的相邻顶点都已经被访问过了,这时他就可以返回,对它来的那个顶点的其余顶点进行搜索。
深度优先搜索的实现可以利用递归很简单地实现。
广度优先搜索相对于深度优先搜索侧重点不一样,
深度优先好比是一个人走迷宫,一次只能选定一条路走下去,
而广度优先搜索好比是一次能够有任意多个人,一次就走到和一个顶点相连的所有未访问过的顶点,然后再从这些顶点出发,继续这个过程。
具体实现的时候我们使用先进先出队列来实现这个过程:
首先将起点加入队列,然后将其出队,把和起点相连的顶点加入队列,
将队首元素v出队并标记他
将和v相连的未标记的元素加入队列,然后继续执行步骤2直到队列为空
广度优先搜索的一个重要作用就是它能够找出最短路径,这个很好理解,因为广度优先搜索相当于每次从一个起点开始向所有可能的方向走一步,那么第一次到达目的地的这个路径一定是最短的,而到达了之后由于这个点已经被访问过而不会再被访问,这个路径就不会被更改了。
广度优先遍历是爬虫中使用最广泛的一种爬虫策略,之所以使用广度优先搜索策略,主要原因有三点:
# 深度优先: 根左右 遍历
# 广度优先: 层次遍历,一层一层遍历
# 深度优先: 根左右 遍历 (递归实现)
def depth_tree(tree_node):
if tree_node is not None:
print(tree_node._data)
if tree_node._left is not None:
return depth_tree(tree_node._left) # 递归遍历
if tree_node._right is not None:
return depth_tree(tree_node._right) # 递归遍历
# 广度优先: 层次遍历,一层一层遍历(队列实现)
def level_queue(root):
if root is None:
return
my_queue = []
node = root
my_queue.append(node) # 根结点入队列
while my_queue:
node = my_queue.pop(0) # 出队列
print(node.elem) # 访问结点
if node.lchild is not None:
my_queue.append(node.lchild) # 入队列
if node.rchild is not None:
my_queue.append(node.rchild) # 入队列
列表法:
# 树的数据结构设计
# 1.列表法
# 简述:列表里包含三个元素:根结点、左结点、右结点
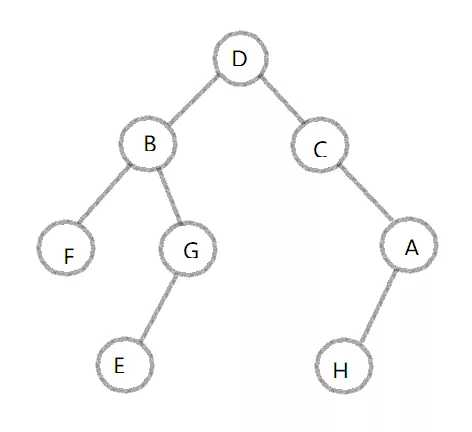
my_Tree = [
‘D‘, # 根结点
[‘B‘,
[‘F‘,[],[]],
[‘G‘,[‘E‘,[],[]],[]]
], # 左子树
[‘C‘,
[],
[‘A‘,[‘H‘,[],[]],[]]
] # 右子树
]
# 列表操作函数
# pop() 函数用于移除列表中的一个元素(默认最后一个元素),并且返回该元素的值。
# insert() 函数用于将指定对象插入列表的指定位置,没有返回值。
# 深度优先: 根左右 遍历 (递归实现)
def depth_tree(tree_node):
if tree_node:
print(tree_node[0])
# 访问左子树
if tree_node[1]:
depth_tree(tree_node[1]) # 递归遍历
# 访问右子树
if tree_node[2]:
depth_tree(tree_node[2]) # 递归遍历
depth_tree(my_Tree)
# result:
# D B F G E C A H
# 广度优先: 层次遍历,一层一层遍历(队列实现)
def level_queue(root):
if not root:
return
my_queue = []
node = root
my_queue.append(node) # 根结点入队列
while my_queue:
node = my_queue.pop(0) # 出队列
print(node[0]) # 访问结点
if node[1]:
my_queue.append(node[1]) # 入队列
if node[2]:
my_queue.append(node[2]) # 入队列
level_queue(my_Tree)
# result :
# D B C F G A E H
方法二:构造类节点法
#2.构造类
# Tree类,类变量root 为根结点,为str类型
# 类变量right/left 为左右节点,为Tree型,默认为空
class Tree:
root = ‘‘
right = None
left = None
# 初始化类
def __init__(self,node):
self.root = node
def set_root(self,node):
self.root = node
def get_root(self):
return self.root
# 初始化树
# 设置所有根结点
a = Tree(‘A‘)
b = Tree(‘B‘)
c = Tree(‘C‘)
d = Tree(‘D‘)
e = Tree(‘E‘)
f = Tree(‘F‘)
g = Tree(‘G‘)
h = Tree(‘H‘)
# 设置节点之间联系,生成树
a.left = h
b.left = f
b.right = g
c.right = a
d.left = b
d.right = c
g.left = e
# 深度优先: 根左右 遍历 (递归实现)
def depth_tree(tree_node):
if tree_node is not None:
print(tree_node.root)
if tree_node.left is not None:
depth_tree(tree_node.left) # 递归遍历
if tree_node.right is not None:
depth_tree(tree_node.right) # 递归遍历
depth_tree(d) # 传入根节点
# result:
# D B F G E C A H
# 广度优先: 层次遍历,一层一层遍历(队列实现)
def level_queue(root):
if root is None:
return
my_queue = []
node = root
my_queue.append(node) # 根结点入队列
while my_queue:
node = my_queue.pop(0) # 出队列
print(node.root) # 访问结点
if node.left is not None:
my_queue.append(node.left) # 入队列
if node.right is not None:
my_queue.append(node.right) # 入队列
level_queue(d)
# result :
# D B C F G A E H
本文摘抄自公众号:简说python,本人一直跟着学习的一个公众号.
标签:并且 not adt info def first queue padding 广度优先搜索
原文地址:https://www.cnblogs.com/jjb1997/p/11403967.html