标签:长度 出现 数组 最大 ast min cpp 部分 相同
每相邻的两个字符间添加一个"#",使所有偶数长度回文子串变成奇数,转化成求奇数长度的回文子串
因为奇+偶=奇,所以通过添加#统一成奇数
bob --> #b#o#b# 回文子串长度为3,处理后为7
noon --> #n#o#o#n# 回文子串长度为4,处理后为9\(P[i]\)数组:以\(i\)点为中心的回文子串的半径
规律:回文子串的长度为半径减1,起始位置为中间位置-半径再除以2
故只要我们找到最大的半径,就可以找到最大的回文子串
# 1 # 2 # 2 # 1 # 2 # 2 #
1 2 1 2 5 2 1 6 1 2 3 2 1
/*
"#2#2#1#2#2#",以中间的 '1' 为中心的回文串半径是6,未添加#号的回文子串为 "22122",长度是5
"#b#o#b#",以中间的 'o' 为中心的回文串的半径是4,而 "bob"的长度是3
"#n#o#o#n#",以最中间的 '#' 为中心的回文串的半径是5,而 "noon" 的长度是4
中间的 '1' 在字符串 "#1#2#2#1#2#2#" 中的位置是7,而半径是6,7-6=1,刚好就是回文子串 "22122" 在原串 "122122" 中的起始位置1
"bob","o" 在 "#b#o#b#" 中的位置是3,但是半径是4,这一减成负的了,所以我们应该至少把中心位置向后移动一位,才能为0,那么我们就需要在前面增加一个字符,这个字符不能是#号,也不能是s中可能出现的字符,所以我们暂且就用'$'吧,这样都不相同的话就不会改变p值了,那么末尾要不要对应的也添加呢,其实不用的,不用加的原因是字符串的结尾标识为 '\0',等于默认加过了。
那此时 "o" 在 "$#b#o#b#" 中的位置是4,半径是4,一减就是0了
中间的 '1' 在字符串 "$#1#2#2#1#2#2#" 中的位置是8,而半径是6,这一减就是2了,而我们需要的是1,所以我们要除以2。之前的 "bob" 因为相减已经是0了,除以2还是0,没有问题。
再来验证一下 "noon",中间的 '#' 在字符串 "$#n#o#o#n#" 中的位置是5,半径也是5,相减并除以2还是0,完美。可以任意试试其他的例子,都是符合这个规律的,最长子串的长度是半径减1,起始位置是中间位置减去半径再除以2。
*/$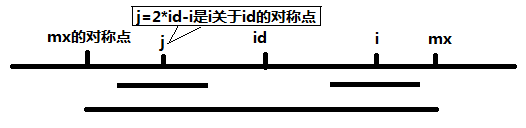
假如\(i<{mx}\) ,求出\(i\)关于\(id\)的对称点\(j=i-2(i-id)=2id-i\) ,在\([mx对称点,mx]\)范围内,\(j\) 两端的值和\(i\)两端的值是完全相同的。
否则\(i\ge{mx}\)时,只能以\(i\)为中心,向两边进行枚举,初始值\(p[i]=1\),然后while循环进行匹配t[i+p[i]]==t[i-p[i]]
string solve(string s){
//预处理
string t = "";
t += "$#";
for(int i=0;i<s.length();i++){
t += s[i];
t += '#';
}
//构造P数组
vector<int> p(t.size(),0);
int mx = 0, id = 0, res_id= 0, res_mx = 0;
//求解
for(int i=1;i<t.size();i++){
//mx>i: 没超过时,求min(p[2id-i],mx-i),再向两边匹配
//i>=mx:超过时,初始化p[i]=1,然后向两边匹配
p[i] = mx > i ? min(p[2*id-i],mx-i):1;
//向两边匹配
while(t[i+p[i]] == t[i-p[i]]) p[i]++;
//更新mx:最右边的回文串的右端,id:最右边回文串的中心位置
if(mx<i+p[i]){ //i+p[i]是当前回文串的右端
mx = i+p[i];
id = i;
}
//更新res_id:最长的回文串的中心,res_mx:最长的回文串的半径
if(res_mx < p[i]){
res_id = i;
rese_mx = p[i];
}
}
return s.substr((res_mx-res_id)/2, res_mx-1);
}标签:长度 出现 数组 最大 ast min cpp 部分 相同
原文地址:https://www.cnblogs.com/doragd/p/11408733.html