首先,在开始介绍数据结构的线性表的链式存储时,我们先来总结下,昨天学习的顺序存储方式,
顺序存储:
顺序存储,说白了就是对数据进行连续的存储,而这可以使用数组进行操作,但是考虑到一般的数组的一些局限性,所以使用动态数组
是不错的选择,这时我们可以使用指针的方式来进行数组上的操作,利用malloc函数来进行申请空间,但是在使用mallo函数的时候,一定记住使用之后要进行free(),避免最后分配空间使用完。
这里我们来总结下顺序存储的优缺点:
1 、优缺点
顺序存储时,相邻数据元素的存放地址也相邻(逻辑与物理统一);要求内存中可用存储单元的地址必须是连续的。
优点:存储密度大(=1),存储空间利用率高。
缺点:插入或删除元素时不方便。
2、 实际应用
(1)顺序表适宜于做查找这样的静态操作,不适合做像链表的插入、删除这样的动态操作。
(2)如果线性表的长度变化不大,且其主要操作是查找,应采用顺序表;
(3)若线性表的长度变化较大,且其主要操作是插入、删除操作,应采用链表。
通过对顺序存储结构的线性表的总结,我们看出,在一般的元素查找时,顺序表很适合,但是当插入、删除这样的操作多的时候,
程序运行就比较费时,所以这时我们提出了链式存储的解决思想。
链式存储:
链式存储时,相邻数据元素可随意存放,但所占存储空间分两部分,一部分存放结点值,另一部分存放表示结点间关系的指针
优点:插入或删除元素时很方便,使用灵活。
缺点:存储密度小(<1),存储空间利用率低
我们今天要介绍的线性表的链式存储结构就可以很好的解决顺序结构的缺点,一起来看
仔细分析后,我们可以发现在顺序存储结构中,他们相邻的元素的存储位置也是相邻的,
我们在申请内存的的时候,是一次性申请一块连续的内存,中间是没有空隙的,这样我们
也就没办法进行快速的插入,如果进行删除操作,就需要进行位置的填充,或者进行插入
的时候需要进行元素的移动,而这都需要花费大量的时间。
链式存储结构之所以能很好地解决这个问题,原因就在于它不考虑存储位置的相邻关系了,
哪里有空位就存到哪里,我们只需要让每个元素都知道下一个元素的位置在哪里就可以了。
这样就是我们在定义链式存储结构的时候,除了定义它本身需要存储的信息之外,还需要存储一个
能够指示它直接后继的一个信息,这个信息我们可以用指针来表示。这也就是我们课本上讲的数据域和指针域。

我们将这种只带有一个指针域的线性表称为单链表。
链表中第一个结点的存储位置叫做头指针。
单链表的第一个结点钱附设一个结点,称为头结点。
上一节我们提到过,线性表的最后一个元素是没有直接后继的,所以在链式存储中,我们将最后一个结点的指针域设置为null.
下面我们来看单链表的具体代码实现
 链式存储结构
链式存储结构//链表结点
typedef struct LINKNODE{
void* date;//数据域
struct LINKNODE* next;//指针域,指向下一个结点的数据域
}LinkNode;
//链表结构体
typedef struct LINKLIST{
int size;//数据个数
LinKNode* head;
}LinkList;
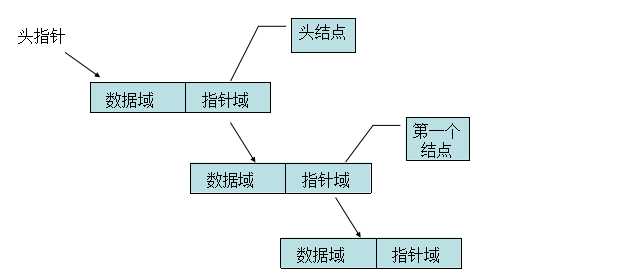
很多同学分不清头指针,头结点,以及第一个结点之间的关系和区别,我们下面简单地区分下。
头指针:是指向链表的指针,如果链表有头结点,它会指向头结点
头结点:第一个结点之前的一个辅助结点,其next指向第一个结点
第一个结点:就是一个结点,data变量存放第一个数据,next指针变量指向第二个结点
这里要注意的就是头指针是一个链表的必要元素,而头结点却不是,那么头结点存在的意义是什么呢?
使第一个结点的插入操作和删除操作和后面结点的操作一致,否则我们在修改第一个结点的时候,就需要修改头指针。
如果没有头结点,头指针直接指向第一个结点。
下面我们来看链式存储结构的具体操作
在进行操作之前我们需要建立一个连式存储结构的链表
下面看初始化操作
 创建链表
创建链表//初始化链表
LinkList* Init_LinkList(){
LinkList* list = (LinkList*)malloc(sizeof(LinkList));
list->size=0;
list->head=(LinkNode*)malloc(sizeof(LinkNode));
list->head->date=NULL;
list->head->next=NULL;
return list;
}
我觉得这个创建链表的方法可以叫插队法,它就是无限在插队,哈哈
 插入操作
插入操作//指定位置进行插入操作
void Insert_LinkLIst(LinkList* list ,int pos,void date){
//加强程序的健壮性
if(list==NULL)
return ;
if(date==NULL)
return ;
//友好处理,判断是否出现越界情况
if(pos<o||pos>list->size)
pos=list->pos;
//创建新结点
LinkNode* newnode=(LinkNode*)malloc(sizeof(LinkNode));
newnode->date=date;
newnode->next=NULL;
//找结点
//建立辅助指针
LinkNode* p=list->head;
for(int i=0;i<pos;i++){
p=p->next;
}
//加入新的结点
newnode->next=p->next;
p->next=newnode;
list->size++;
}
写完代码之后,我们一起来整理下插入结点的思路:
- 声明一个指针p指向链表的头结点
- 循环遍历,找到插入的位置,让p的指针不断向后移动,不断指向下一个结点,计数变量i累加
- 判断插入位置的合理性
- 生成新结点
- 将要插入的值赋给新结点的数据域
- 单链表插入的重点:newNode->next = p->next; p->next = newNode;
- 成功
接下来看链式存储的删除操作
 删除操作
删除操作////删除指定位置的元素
vid RemoveByPos(LinkList* list,int pos){
if(list==NULL)
return;
if(pos<0||pos>list->size)
return ;
//建立辅助指针,找到指定位置的前一个结点
LinkNode* p=list->head;
for(int i=0;i<pos;i++){
p=p->nest;
}
//找出当前指定位置的结点
//缓存删除结点
LinkNode* pD = p->next;
p->next = pD->next;
//释放删除结点
free(pD);
list->size--;
}
整理一下删除结点的思路:声明指针p指向链表的头结点
- 循环遍历查找要删除的位置,计算变量累加
- 判断删除位置的合理性,如果要删除的结点的后继为空,则位置不合理
- 将要删除的结点p->next 赋值给q
- 单链表删除语句 p->next = q->next
- 赋值
- 释放内存
- 成功
写完插入和删除操作,我们便可以看出,链式存储结构对于插入和删除的优势是明显的,不需要进行大量的元素的移动。
增删改查,增和删给大家说完了,下面来说改和查,个人感觉这两个其实差不多,改就是比查多了个修改元素,所以这里我只给大家贴一个查的代码了
 查找操作
查找操作
//查询操作
int Find_LinkList(LinkList* list,void* date){
if(list==NLL)
return ;
if(date==NULL)
return 0;
//建立辅助指针
LinkNode* p=list->head->next;
int i=0;
while(p!=NULL){
if(p->date==date)
break;
i++;
p=p->next;
}
return i;
}
观察查找操作,大家就会发现,链式存储结构也是有其缺点的,其不便于进行查找和修改
到这里,我们的链式存储就算是讲完了,最后将顺序存储结构和链表存储结构进行一下对比
我们主要从两个方面进行对比,一个是时间,一个是空间
时间:
- 查找
顺序存储结构 O{1}
链式存储结构O{n}
- 插入和删除
顺序存储结构 O{n}
链式存储结构O{1}
空间:
- 顺序存储结构:需要提前分配空间大小,分配打了,产生碎片,浪费,分配小了,容易导致溢出
- 连式存储结构:不需要预分配,只要有就可以分配,并且数量不受变量限制
从以上比较不难看出
1、若线性表需要频繁的查找,很少进行插入和删除操作的时候,应该采用顺序存储。相反,则应采用链式存储结构
2、当线性表不知道到底有多大的时候,建议采用链式存储结构,如果我们已经提前知道其大小,可采用顺序存储结构
3、顺序存储结构和链式存储结构各有各的优缺点,不能一概而论说就是哪种更好。我们需要根据实际情况来选择我们需要的结构
线性表到这里就算是结束了,接下来会带大家一起学习队列。
