标签:这不 说明 越界 最坏情况 step 不同 struct input com
问题描述:
有一个矩形稻田,每天晚上,青蛙会从一侧跳进稻田从而踩坏稻子,规定:每只青蛙总沿着一条直线跳跃,且每只青蛙每次跳跃距离相同(不同青蛙的蛙跳步长不同 ,不同青蛙的蛙跳 方向可能不同)
稻田里的稻子组成一个栅格, 每棵稻子位于一个格点上 ,而青蛙总是从稻田的一侧跳进稻田, 然后沿着某条直线穿 越稻田, 从另一侧跳出去,如图: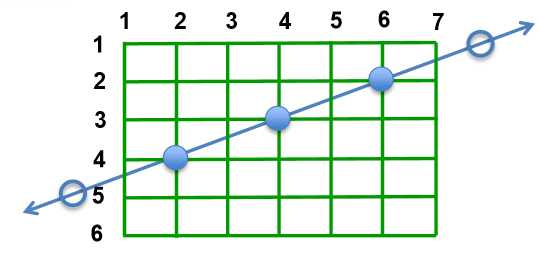
农民想知道那只踩了最多稻子的青蛙的跳跃轨迹,请给出该轨迹上踩的稻子数(规定一条路径上稻子数至少为3)
输入:
第一行上两个整数R, C, 分别表示稻田中水稻的行数和 列数, 1≤R, C≤5000 ;第二行是一个整数N, 表示被踩踏的水稻数量, 3≤N≤5000 ;在剩下的N行中, 每行有两个整数, 分别是一颗被踩踏水 稻的行号(1~R)和列号(1~C), 两个整数用一个空格隔开 ;且每棵被踩踏水稻只被列出一次
输出:
如果在稻田中存在青蛙行走路径, 则输出包含最多水稻 的青蛙行走路径中的水稻数量, 否则输出0
示例:

分析:
首先,自然想到枚举算法,由于稻田是有限的,或者说,被破坏的稻子数量是有限的(不超过5000),对于一条路径,我们如何确定它?从三个方面考虑:起始点,方向,步长。似乎可行,但简单分析可以知道,最坏情况下,需要付出5000*5000*5000的代价,这不能令人满意。因此,必须设法缩小解空间。
如果我们从踩坏的稻子序列中,拿出两个,假设一个是第一个跳跃点,一个是第二个跳跃点。在这种假设下,我们得到跳跃步长(作减法即可,注意x、y两个方向上的向量分解),然后根据一些必要条件,判断是否是可能解,如果不是则提前从解空间中删除该解,进入下一个枚举。如果满足必要条件,则需要计算该走法的情况下的踩坏的稻子数,如果比既定的max大,则更新Max,否则继续下一轮枚举。
必要条件说明:
根据第一个点坐标 和 计算得到的步长,计算第一个点的前一个点,是否落在稻田内,如果是,则假设不正确,continue
为了避免无效计算,可根据假定的max,从x和y两个角度判断是否可能比max大,如果提早越界,则作相应处理,因为不可能是有效解(说明:本算法中对x作了排列,因此这不是由第二个点导致的,而是第一个点的问题)
代码(c++):
1 #include <stdio.h> 2 #include <stdlib.h> 3 #include <algorithm> 4 using namespace std; 5 int r, c, n; 6 struct PLANT { 7 int x, y; 8 }; 9 PLANT plants[5001]; 10 11 int searchPath(PLANT, int, int); 12 13 int main() 14 { 15 freopen("input2.txt", "r", stdin); 16 int max = 2, steps; 17 scanf("%d %d %d", &r, &c, &n); 18 for (int i = 0; i < n; ++i) 19 scanf("%d %d", &plants[i].x, &plants[i].y); 20 //input end 21 sort(plants, plants + n); 22 for (int i = 0; i < n-2; ++i) 23 for (int j = i + 1; j < n-1; ++j) { 24 int dX = plants[j].x - plants[i].x; 25 int dY = plants[j].y - plants[i].y; 26 int pX = plants[i].x - dX; 27 int pY = plants[i].y - dY; 28 if (pX >= 1 && pX <= r && pY >= 1 && pY <= c) 29 continue; 30 if (plants[i].x + (max - 1)*dX > r) 31 break; 32 pY = plants[i].y + (max - 1)*dY; 33 if (pY > c || pY < 1) 34 continue; 35 steps = searchPath(plants[j], dX, dY); 36 if (steps > max) 37 max = steps; 38 } 39 if (max == 2) 40 max = 0; 41 printf("%d\n", max); 42 } 43 44 int searchPath(PLANT p, int dX, int dY) 45 { 46 PLANT q; 47 q.x = p.x + dX; 48 q.y = p.y + dY; 49 int steps = 2; 50 while (q.x <= r && q.x >= 1 && q.y <= c && q.x >= 1) { 51 if (!binary_search(plants, plants + n, q)) { 52 steps = n; 53 break; 54 } 55 q.x += dX; 56 q.y += dY; 57 steps++; 58 } 59 return steps; 60 } 61 62 bool operator<(const PLANT & p1, const PLANT & p2) 63 { 64 if (p1.x == p2.x) { 65 return p1.y < p2.y; 66 } 67 return p1.x < p2.x; 68 }
标签:这不 说明 越界 最坏情况 step 不同 struct input com
原文地址:https://www.cnblogs.com/laideng/p/11437228.html