标签:代码执行 超过 下标 例子 创建 虚拟 空间 cpu http

算法为王。
想学好前端,先练好内功,只有内功深厚者,前端之路才会走得更远。
笔者写的 JavaScript 数据结构与算法之美 系列用的语言是 JavaScript ,旨在入门数据结构与算法和方便以后复习。
之所以把归并排序、快速排序、希尔排序、堆排序放在一起比较,是因为它们的平均时间复杂度都为 O(nlogn)。
请大家带着问题:快排和归并用的都是分治思想,递推公式和递归代码也非常相似,那它们的区别在哪里呢 ? 来阅读下文。
思想
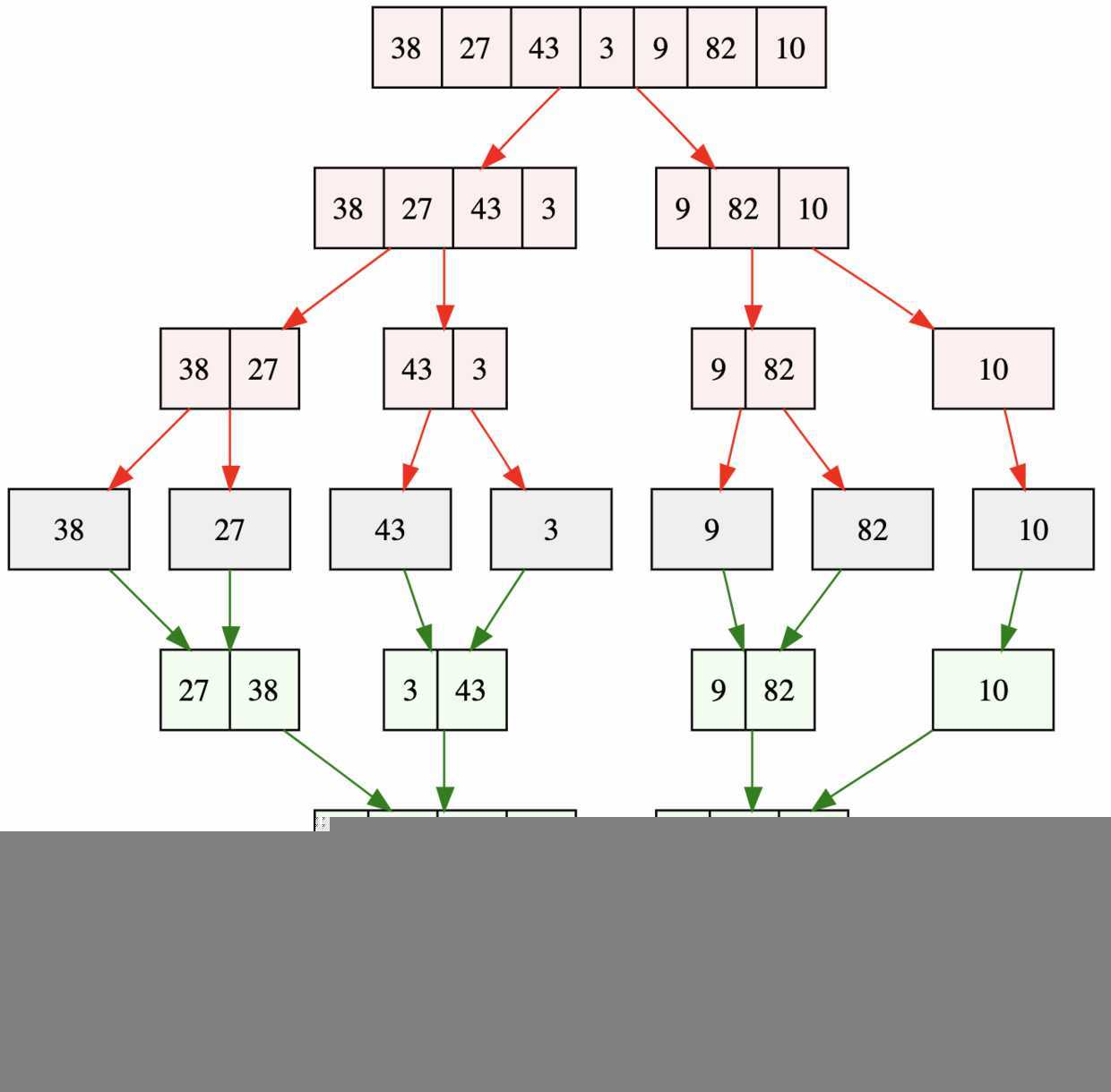
排序一个数组,我们先把数组从中间分成前后两部分,然后对前后两部分分别排序,再将排好序的两部分合并在一起,这样整个数组就都有序了。
归并排序采用的是分治思想。
分治,顾名思义,就是分而治之,将一个大问题分解成小的子问题来解决。小的子问题解决了,大问题也就解决了。
注:x >> 1 是位运算中的右移运算,表示右移一位,等同于 x 除以 2 再取整,即 x >> 1 === Math.floor(x / 2) 。
实现
const mergeSort = arr => {
//采用自上而下的递归方法
const len = arr.length;
if (len < 2) {
return arr;
}
// length >> 1 和 Math.floor(len / 2) 等价
let middle = Math.floor(len / 2),
left = arr.slice(0, middle),
right = arr.slice(middle); // 拆分为两个子数组
return merge(mergeSort(left), mergeSort(right));
};
const merge = (left, right) => {
const result = [];
while (left.length && right.length) {
// 注意: 判断的条件是小于或等于,如果只是小于,那么排序将不稳定.
if (left[0] <= right[0]) {
result.push(left.shift());
} else {
result.push(right.shift());
}
}
while (left.length) result.push(left.shift());
while (right.length) result.push(right.shift());
return result;
};测试
// 测试
const arr = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48];
console.time('归并排序耗时');
console.log('arr :', mergeSort(arr));
console.timeEnd('归并排序耗时');
// arr : [2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]
// 归并排序耗时: 0.739990234375ms分析
第一,归并排序是原地排序算法吗 ?
这是因为归并排序的合并函数,在合并两个有序数组为一个有序数组时,需要借助额外的存储空间。
实际上,尽管每次合并操作都需要申请额外的内存空间,但在合并完成之后,临时开辟的内存空间就被释放掉了。在任意时刻,CPU 只会有一个函数在执行,也就只会有一个临时的内存空间在使用。临时内存空间最大也不会超过 n 个数据的大小,所以空间复杂度是 O(n)。
所以,归并排序不是原地排序算法。
第二,归并排序是稳定的排序算法吗 ?
merge 方法里面的 left[0] <= right[0] ,保证了值相同的元素,在合并前后的先后顺序不变。归并排序是一种稳定的排序方法。
第三,归并排序的时间复杂度是多少 ?
从效率上看,归并排序可算是排序算法中的佼佼者。假设数组长度为 n,那么拆分数组共需 logn 步, 又每步都是一个普通的合并子数组的过程,时间复杂度为 O(n),故其综合时间复杂度为 O(nlogn)。
最佳情况:T(n) = O(nlogn)。
最差情况:T(n) = O(nlogn)。
平均情况:T(n) = O(nlogn)。
动画
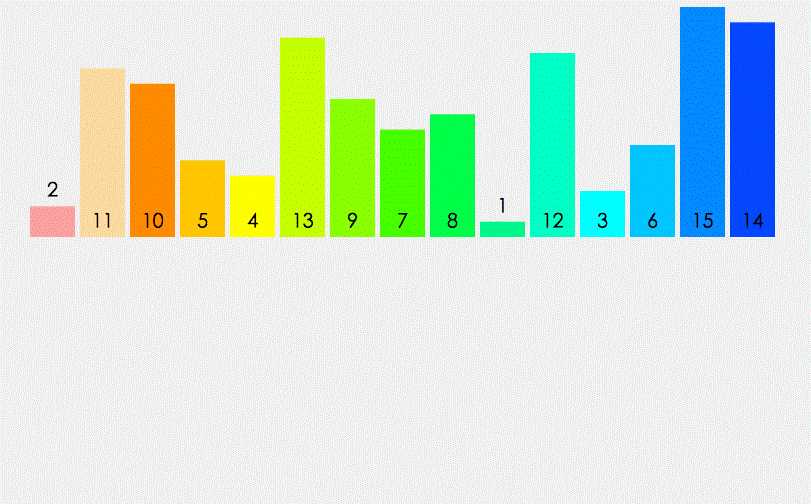
快速排序的特点就是快,而且效率高!它是处理大数据最快的排序算法之一。
思想
特点:快速,常用。
缺点:需要另外声明两个数组,浪费了内存空间资源。
实现
方法一:
const quickSort1 = arr => {
if (arr.length <= 1) {
return arr;
}
//取基准点
const midIndex = Math.floor(arr.length / 2);
//取基准点的值,splice(index,1) 则返回的是含有被删除的元素的数组。
const valArr = arr.splice(midIndex, 1);
const midIndexVal = valArr[0];
const left = []; //存放比基准点小的数组
const right = []; //存放比基准点大的数组
//遍历数组,进行判断分配
for (let i = 0; i < arr.length; i++) {
if (arr[i] < midIndexVal) {
left.push(arr[i]); //比基准点小的放在左边数组
} else {
right.push(arr[i]); //比基准点大的放在右边数组
}
}
//递归执行以上操作,对左右两个数组进行操作,直到数组长度为 <= 1
return quickSort1(left).concat(midIndexVal, quickSort1(right));
};
const array2 = [5, 4, 3, 2, 1];
console.log('quickSort1 ', quickSort1(array2));
// quickSort1: [1, 2, 3, 4, 5]方法二:
// 快速排序
const quickSort = (arr, left, right) => {
let len = arr.length,
partitionIndex;
left = typeof left != 'number' ? 0 : left;
right = typeof right != 'number' ? len - 1 : right;
if (left < right) {
partitionIndex = partition(arr, left, right);
quickSort(arr, left, partitionIndex - 1);
quickSort(arr, partitionIndex + 1, right);
}
return arr;
};
const partition = (arr, left, right) => {
//分区操作
let pivot = left, //设定基准值(pivot)
index = pivot + 1;
for (let i = index; i <= right; i++) {
if (arr[i] < arr[pivot]) {
swap(arr, i, index);
index++;
}
}
swap(arr, pivot, index - 1);
return index - 1;
};
const swap = (arr, i, j) => {
let temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
};测试
// 测试
const array = [5, 4, 3, 2, 1];
console.log('原始array:', array);
const newArr = quickSort(array);
console.log('newArr:', newArr);
// 原始 array: ?[5, 4, 3, 2, 1]
// newArr: ? [1, 4, 3, 2, 5]分析
第一,快速排序是原地排序算法吗 ?
因为 partition() 函数进行分区时,不需要很多额外的内存空间,所以快排是原地排序算法。
第二,快速排序是稳定的排序算法吗 ?
和选择排序相似,快速排序每次交换的元素都有可能不是相邻的,因此它有可能打破原来值为相同的元素之间的顺序。因此,快速排序并不稳定。
第三,快速排序的时间复杂度是多少 ?
极端的例子:如果数组中的数据原来已经是有序的了,比如 1,3,5,6,8。如果我们每次选择最后一个元素作为 pivot,那每次分区得到的两个区间都是不均等的。我们需要进行大约 n 次分区操作,才能完成快排的整个过程。每次分区我们平均要扫描大约 n / 2 个元素,这种情况下,快排的时间复杂度就从 O(nlogn) 退化成了 O(n2)。
最佳情况:T(n) = O(nlogn)。
最差情况:T(n) = O(n2)。
平均情况:T(n) = O(nlogn)。
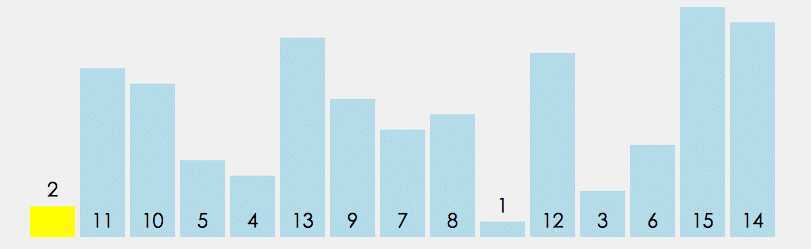
动画
解答开篇问题
快排和归并用的都是分治思想,递推公式和递归代码也非常相似,那它们的区别在哪里呢 ?
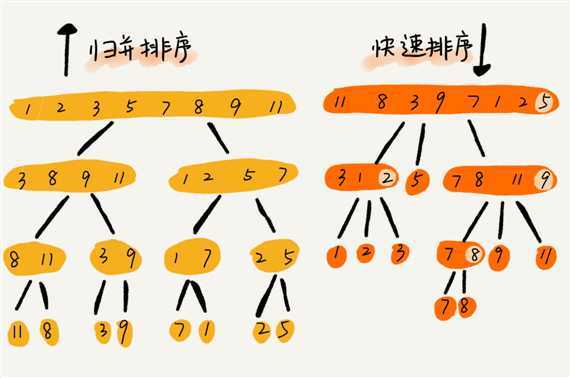
可以发现:
由下而上的,先处理子问题,然后再合并。由上而下的,先分区,然后再处理子问题。思想
过程
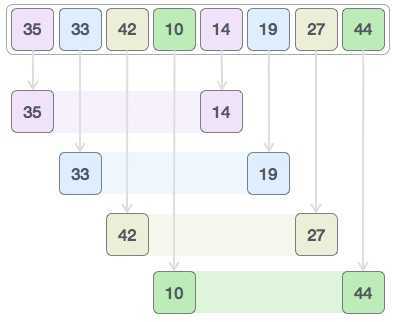

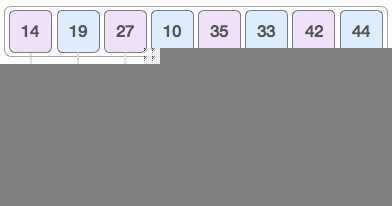

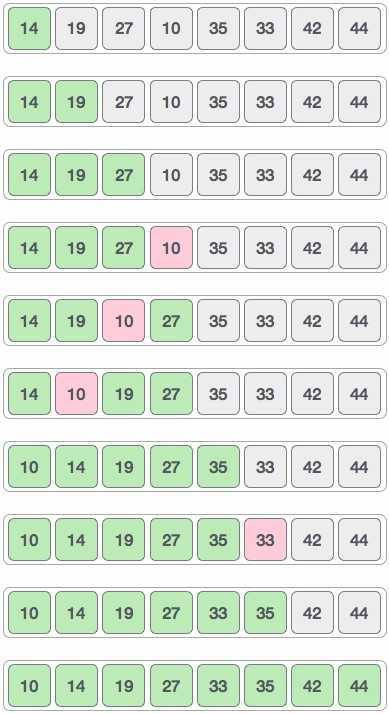
实现
const shellSort = arr => {
let len = arr.length,
temp,
gap = 1;
console.time('希尔排序耗时');
while (gap < len / 3) {
//动态定义间隔序列
gap = gap * 3 + 1;
}
for (gap; gap > 0; gap = Math.floor(gap / 3)) {
for (let i = gap; i < len; i++) {
temp = arr[i];
let j = i - gap;
for (; j >= 0 && arr[j] > temp; j -= gap) {
arr[j + gap] = arr[j];
}
arr[j + gap] = temp;
console.log('arr :', arr);
}
}
console.timeEnd('希尔排序耗时');
return arr;
};测试
// 测试
const array = [35, 33, 42, 10, 14, 19, 27, 44];
console.log('原始array:', array);
const newArr = shellSort(array);
console.log('newArr:', newArr);
// 原始 array: ??[35, 33, 42, 10, 14, 19, 27, 44]
// arr : ??[14, 33, 42, 10, 35, 19, 27, 44]
// arr : ??[14, 19, 42, 10, 35, 33, 27, 44]
// arr : ??[14, 19, 27, 10, 35, 33, 42, 44]
// arr : ??[14, 19, 27, 10, 35, 33, 42, 44]
// arr : ??[14, 19, 27, 10, 35, 33, 42, 44]
// arr : ??[14, 19, 27, 10, 35, 33, 42, 44]
// arr : ??[10, 14, 19, 27, 35, 33, 42, 44]
// arr : ??[10, 14, 19, 27, 35, 33, 42, 44]
// arr : ??[10, 14, 19, 27, 33, 35, 42, 44]
// arr : ??[10, 14, 19, 27, 33, 35, 42, 44]
// arr : ??[10, 14, 19, 27, 33, 35, 42, 44]
// 希尔排序耗时: 3.592041015625ms
// newArr: ? [10, 14, 19, 27, 33, 35, 42, 44]分析
第一,希尔排序是原地排序算法吗 ?
希尔排序过程中,只涉及相邻数据的交换操作,只需要常量级的临时空间,空间复杂度为 O(1) 。所以,希尔排序是原地排序算法。
第二,希尔排序是稳定的排序算法吗 ?
我们知道,单次直接插入排序是稳定的,它不会改变相同元素之间的相对顺序,但在多次不同的插入排序过程中,相同的元素可能在各自的插入排序中移动,可能导致相同元素相对顺序发生变化。
因此,希尔排序不稳定。
第三,希尔排序的时间复杂度是多少 ?
最佳情况:T(n) = O(n log n)。
最差情况:T(n) = O(n log2 n)。
平均情况:T(n) = O(n log2 n)。
动画
堆的定义
堆其实是一种特殊的树。只要满足这两点,它就是一个堆。
对于每个节点的值都大于等于子树中每个节点值的堆,我们叫作大顶堆。
对于每个节点的值都小于等于子树中每个节点值的堆,我们叫作小顶堆。
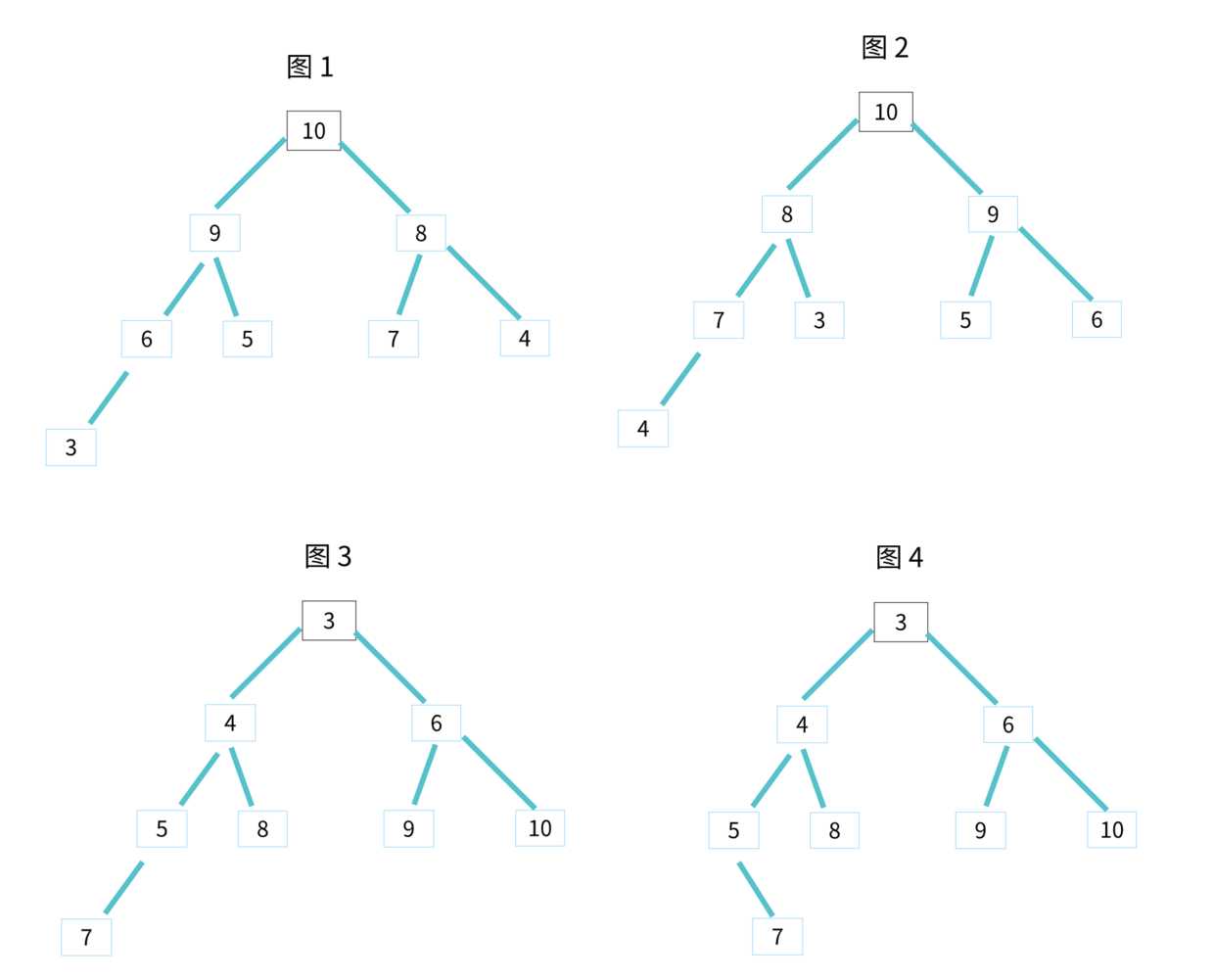
其中图 1 和 图 2 是大顶堆,图 3 是小顶堆,图 4 不是堆。除此之外,从图中还可以看出来,对于同一组数据,我们可以构建多种不同形态的堆。
思想
实现
// 堆排序
const heapSort = array => {
console.time('堆排序耗时');
// 初始化大顶堆,从第一个非叶子结点开始
for (let i = Math.floor(array.length / 2 - 1); i >= 0; i--) {
heapify(array, i, array.length);
}
// 排序,每一次 for 循环找出一个当前最大值,数组长度减一
for (let i = Math.floor(array.length - 1); i > 0; i--) {
// 根节点与最后一个节点交换
swap(array, 0, i);
// 从根节点开始调整,并且最后一个结点已经为当前最大值,不需要再参与比较,所以第三个参数为 i,即比较到最后一个结点前一个即可
heapify(array, 0, i);
}
console.timeEnd('堆排序耗时');
return array;
};
// 交换两个节点
const swap = (array, i, j) => {
let temp = array[i];
array[i] = array[j];
array[j] = temp;
};
// 将 i 结点以下的堆整理为大顶堆,注意这一步实现的基础实际上是:
// 假设结点 i 以下的子堆已经是一个大顶堆,heapify 函数实现的
// 功能是实际上是:找到 结点 i 在包括结点 i 的堆中的正确位置。
// 后面将写一个 for 循环,从第一个非叶子结点开始,对每一个非叶子结点
// 都执行 heapify 操作,所以就满足了结点 i 以下的子堆已经是一大顶堆
const heapify = (array, i, length) => {
let temp = array[i]; // 当前父节点
// j < length 的目的是对结点 i 以下的结点全部做顺序调整
for (let j = 2 * i + 1; j < length; j = 2 * j + 1) {
temp = array[i]; // 将 array[i] 取出,整个过程相当于找到 array[i] 应处于的位置
if (j + 1 < length && array[j] < array[j + 1]) {
j++; // 找到两个孩子中较大的一个,再与父节点比较
}
if (temp < array[j]) {
swap(array, i, j); // 如果父节点小于子节点:交换;否则跳出
i = j; // 交换后,temp 的下标变为 j
} else {
break;
}
}
};测试
const array = [4, 6, 8, 5, 9, 1, 2, 5, 3, 2];
console.log('原始array:', array);
const newArr = heapSort(array);
console.log('newArr:', newArr);
// 原始 array: ?[4, 6, 8, 5, 9, 1, 2, 5, 3, 2]
// 堆排序耗时: 0.15087890625ms
// newArr: ? [1, 2, 2, 3, 4, 5, 5, 6, 8, 9]分析
第二,堆排序是稳定的排序算法吗 ?
因为在排序的过程,存在将堆的最后一个节点跟堆顶节点互换的操作,所以就有可能改变值相同数据的原始相对顺序。
所以,堆排序是不稳定的排序算法。
第三,堆排序的时间复杂度是多少 ?
堆排序包括建堆和排序两个操作,建堆过程的时间复杂度是 O(n),排序过程的时间复杂度是 O(nlogn),所以,堆排序整体的时间复杂度是 O(nlogn)。
最佳情况:T(n) = O(nlogn)。
最差情况:T(n) = O(nlogn)。
平均情况:T(n) = O(nlogn)。
动画
复杂性对比
| 名称 | 平均 | 最好 | 最坏 | 空间 | 稳定性 | 排序方式 |
|---|---|---|---|---|---|---|
| 归并排序 | O(n log n) | O(n log n) | O(n log n) | O(n) | Yes | Out-place |
| 快速排序 | O(n log n) | O(n log n) | O(n2) | O(logn) | No | In-place |
| 希尔排序 | O(n log n) | O(n log2 n) | O(n log2 n) | O(1) | No | In-place |
| 堆排序 | O(n log n) | O(n log n) | O(n log n) | O(1) | No | In-place |
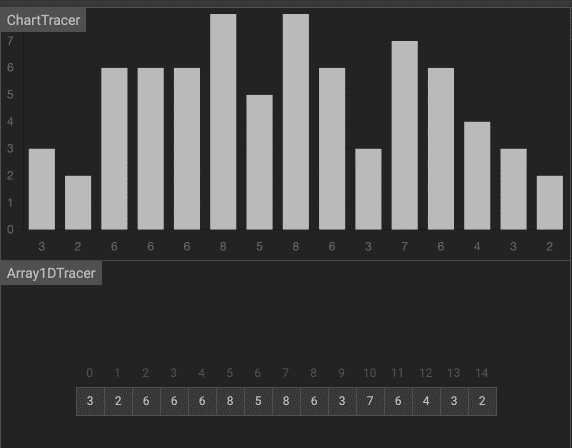
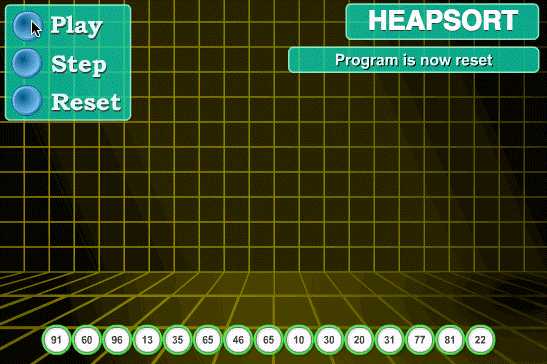
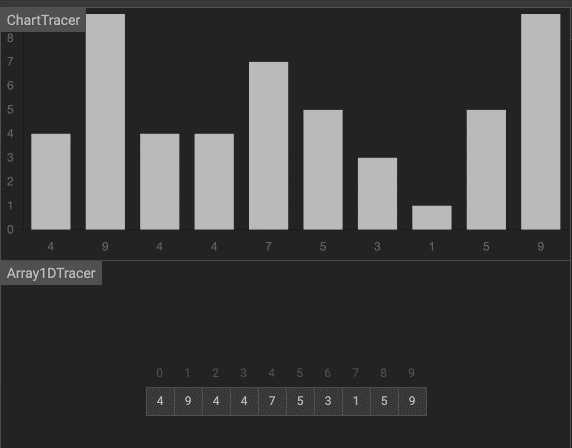
算法可视化工具
效果如下图。
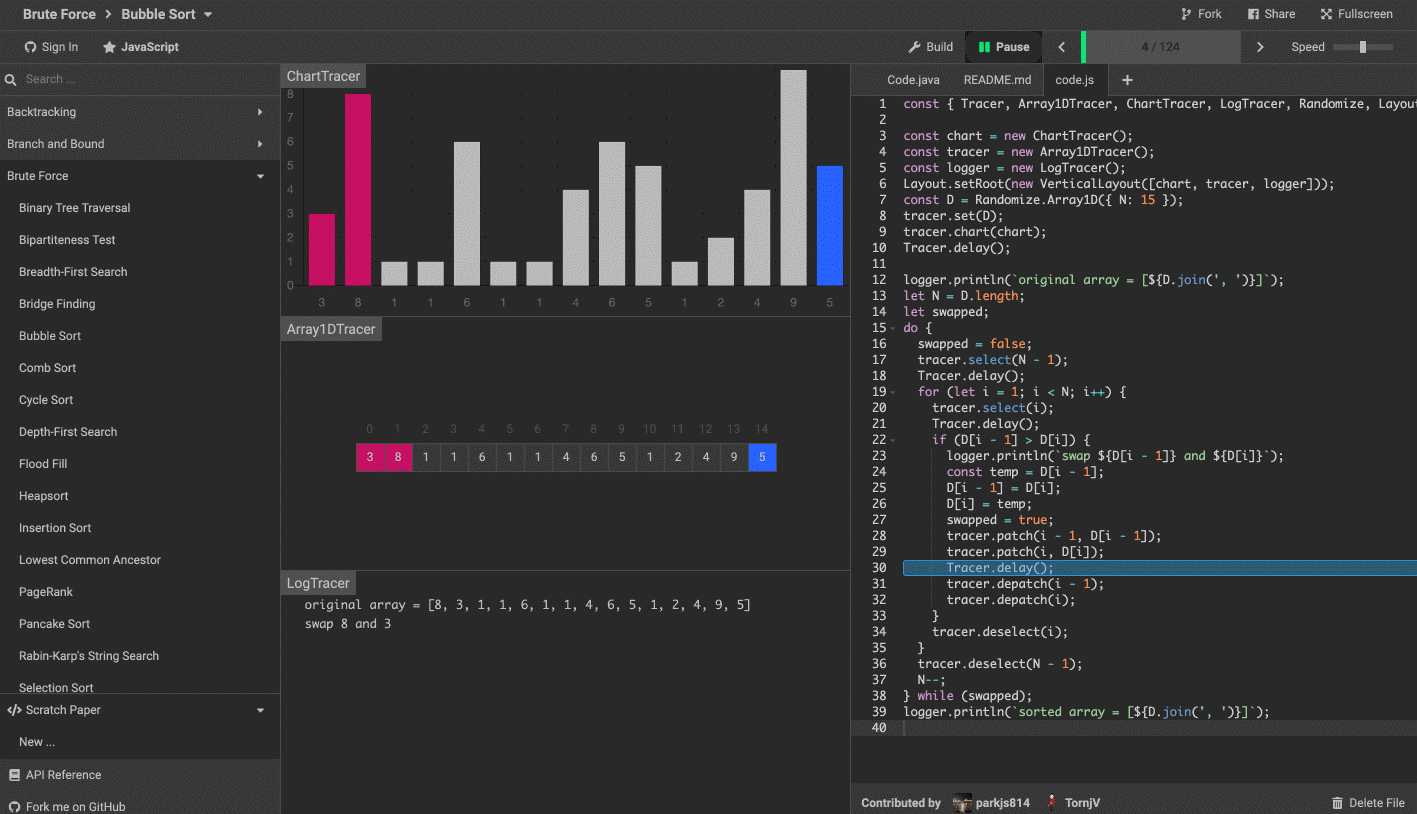
旨在通过交互式可视化的执行来揭示算法背后的机制。
算法可视化来源 https://visualgo.net/en
效果如下图。
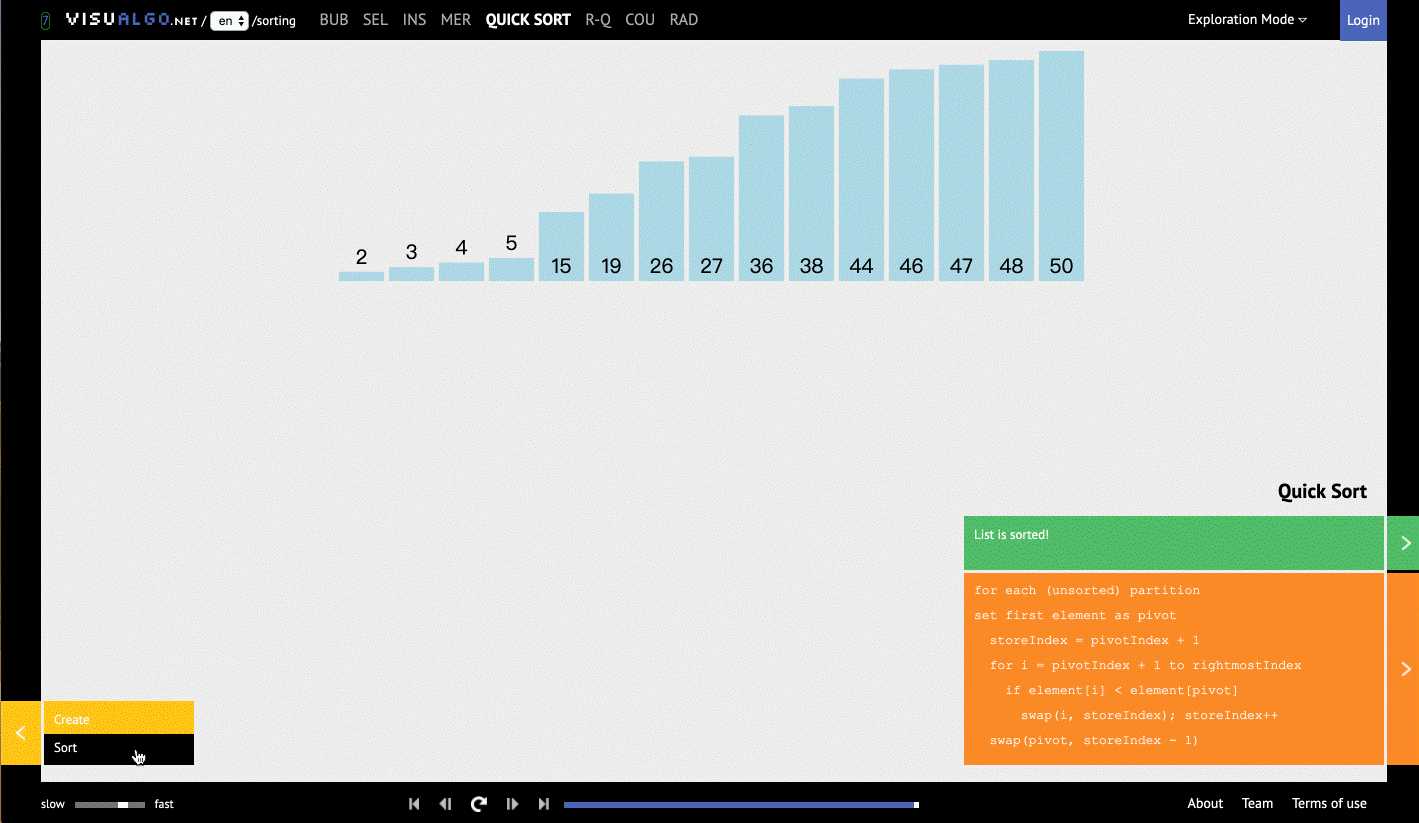
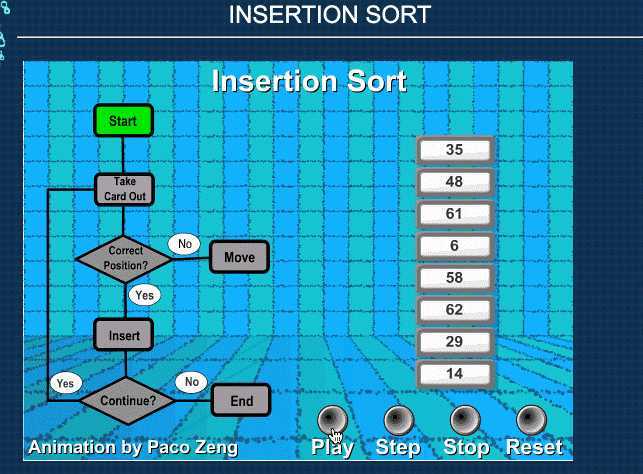
变量和操作的可视化表示增强了控制流和实际源代码。您可以快速前进和后退执行,以密切观察算法的工作方式。

文中所有的代码及测试事例都已经放到我的 GitHub 上了。
觉得有用 ?喜欢就收藏,顺便给个小星星吧。
参考文章:
JavaScript 数据结构与算法之美 - 归并排序、快速排序、希尔排序、堆排序
标签:代码执行 超过 下标 例子 创建 虚拟 空间 cpu http
原文地址:https://www.cnblogs.com/biaochenxuying/p/11450941.html