标签:idt matrix 综合 cte 平方根 预测算法 目标 有序 算法
分类与预测模型对训练集进行预测而得出的准确率并不能很好地反映预测模型未来的性能,为了有效判断一个预测模型的性能表现,需要一组没有参与预测模型建立的数据集,并在该数据集上评价预测模型的准确率,这组独立的数据集叫做测试集。模型预测效果评价,通常用相对/绝对误差、平均绝对误差、均方误差、均方根误差、平均绝对百分误差等指标来衡量。
1、绝对误差与相对误差
设$Y$表示实际值,$\hat{Y}$表示预测值,则$E$为绝对误差,其计算公式为:$E=Y-\hat{Y}$
$e$为相对误差,其计算公式为:$e=\frac{Y-\hat{Y}}{Y}$
2、平均绝对误差
平均误差的计算公式为:$MAE=\frac{1}{n} \sum_{i=1}^{n}\left|E_{i}\right|=\frac{1}{n} \sum_{i=1}^{n}\left|Y_{i}-\hat{Y}_{i}\right|$
其中,$MAE$表示平均绝对误差,$E_{i}$表示第$i$个实际值与预测值的绝对误差,$Y_{\mathrm{i}}$表示第$i$个实际值,$\hat{Y}_{i}$表示第$i$个预测值。
由于预测误差有正有负,为了避免正负相抵消,故取误差的绝对值进行综合并取其平均数,这是误差分析的综合指标法之一。
3、均方误差
均方误差的计算公式为:$MSE=\frac{1}{n} \sum_{i=1}^{n} E_{i}^{2}=\frac{1}{n} \sum_{i=1}^{n}\left(Y_{i}-\hat{Y}_{i}\right)^{2}$
其中,MSE表示均方差。均方误差一般用于还原平方失真程度。均方误差是预测误差平方之和的平均数,它避免了正负误差不能相加的问题。
由于对误差E进行了平方,加强了数值大的误差在指标中的作用,从而提高了这个指标的灵敏性,是一大优点。均方误差是误差分析的综合指标之一。
4、均方根误差
均方根误差的计算公式为:$RMSE=\sqrt{\frac{1}{n} \sum_{i=1}^{n} E_{i}^{2}}=\sqrt{\frac{1}{n} \sum_{i=1}^{n}\left(Y_{i}-\hat{Y}_{i}\right)^{2}}$
其中,RMSE表示均方根误差,其他符号同前。
这是均方误差的平方根,代表了预测值的离散程度,也叫标准误差,最佳拟合情况为$RMSE$=0。均方根误差也是误差分析的综合指标之一。
5、平均绝对百分误差
平均绝对百分误差为:$MAPE=\frac{1}{n} \sum_{i=1}^{n}\left|E_{i} / Y_{i}\right|=\frac{1}{n} \sum_{i=1}^{n}\left|\left(Y_{i}-\hat{Y}_{i}\right) / Y_{i}\right|$
其中,MAPE表示平均绝对百分误差。一般认为MAPE小于10时,预测精度较高。
6、Kappa统计
Kappa统计是比较两个或多个观测者对同一事物,或观测者对同一事物的两次或多次观测结果是否一致,是以由于机遇造成的一致性和实际观测的一致性之间的差别大小作为评价基础的统计指标。Kappa统计量和加权Kappa统计量不但可以用于无序和有序分类变量资料的一致性、重现性检验,而且能给出一个反映一致性大小的“量”值。
Kappa取值在[-1,+1]之间,其值的大小均有不同的意义:
Kappa=+1,说明两次判断的结果完全一致。
Kappa=-1,说明两次判断的结果完全不一致。
Kappa=0,说明两次判断的结果是机遇造成的。
Kappa<0,说明一致程度比机遇造成的还差,两次检查结果很不一致,在实际应用中无意义。
Kappa>0,说明有意义,Kappa越大,说明一致性愈好。
Kappa≥0.75,说明已经取得了相当满意的一致程度。
Kappa<0.4,说明一致程度不够。
7、识别准确度
识别精确度的计算公式为:$\text {Accuracy}=\frac{T P+F N}{T P+T N+F P+F N} \times 100 \%$
其中各项的含义:
TP(True Positives):正确的肯定,表示正确肯定的分类数。
TN(True Negatives):正确的否定,表示正确否定的分类数。
FP(False Positives):错误的肯定,表示错误肯定的分类数。
FN(False Negatives):错误的否定,表示错误否定的分类数。
8、识别精确率
识别精确率的计算公式为:$\text { Precision }=\frac{T P}{T P+F P} \times 100 \%$
9、反馈率
反馈率的计算公式为:$\text {Recall}=\frac{T P}{T P+T N} \times 100 \%$
10、ROC曲线
受试者工作特性(Receiver Operating Characteristic,ROC)曲线,得此名的原因在于曲线上各点反映着相同的感受性,它们都是对同一信号刺激的反应,只不过是在几种不同的判定标准下所得的结果而已。接受者操作特性曲线就是以虚惊概率为横轴,击中概率为纵轴所组成的坐标图,和被试在特定刺激条件下由于采用不同的判断标准得出的不同结果画出的曲线。
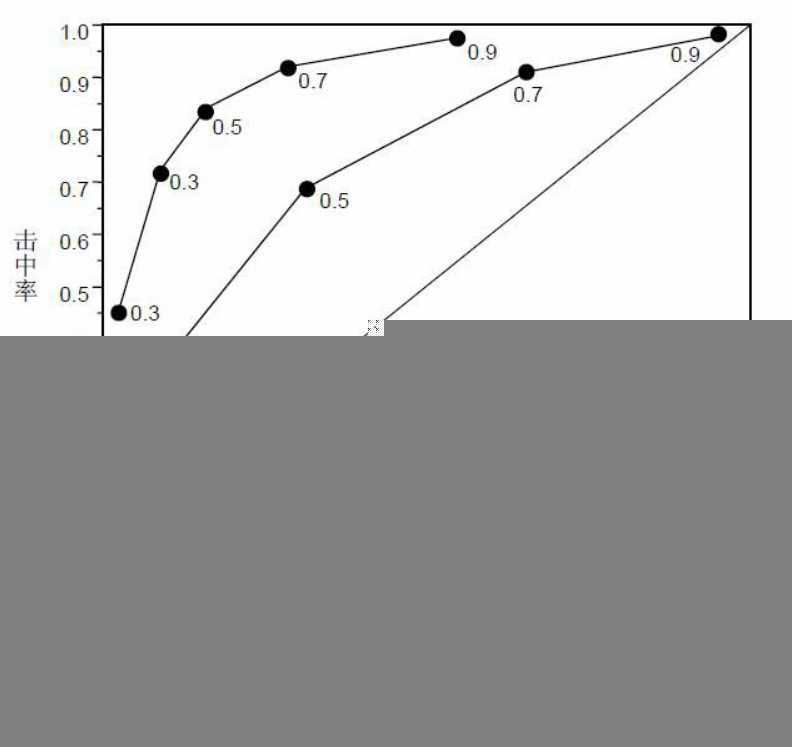
这是一种非常有效的模型评价方法,可为选定临界值给出定量提示。将灵敏度(Sensitivity)设在纵轴,1-特异性(1-Specificity)设在横轴,就可得出ROC曲线图。该曲线下的积分面积(Area)大小与每种方法的优劣密切相关,反映分类器正确分类的统计概率,其值越接近1说明该算法的效果越好。
11、混淆矩阵
混淆矩阵(Confusion Matrix)是模式识别领域中一种常用的表达形式。它描绘样本数据的真实属性与识别结果类型之间的关系,是评价分类器性能的一种常用方法。假设对于N类模式的分类任务,识别数据集D包括$T_{0}$个样本,每类模式分别含有$T_{i}$个数据(i=1…N)。采用某种识别算法构造分类器$C$,$c m_{i j}$,表示第$i$类模式被分类器$C$判断成第$j$类模式的数据占第$i$类模式样本总数的百分率,则可得到如下N·N维混淆矩阵:$$C M(C, D)=\left(\begin{array}{ccccc}{c m_{11}} & {c m_{22}} & {\dots} & {c m_{1 i}} & {\dots} & {c m_{1 N}} \\ {c m_{21}} & {c m_{22}} & {\dots} & {c m_{2 i}} & {\dots} & {c m_{2 N}} \\ {\vdots} & {\vdots} & {} & {\vdots} & {} \\ {c m_{i 1}} & {c m_{i 2}} & {\dots} & {c m_{i i}} & {\dots} & {c m_{i N}} \\ {\vdots} & {\vdots} & {} & {\vdots} & {} \\ {c m_{N 1}} & {c m_{N 2}} & {\dots} & {c m_{N i}} & {\dots} & {c m_{N N}}\end{array}\right)$$
混淆矩阵中元素的行下标对应目标的真实属性,列下标对应分类器产生的识别属性。对角线元素表示各模式能够被分类器C正确识别的百分率,而非对角线元素则表示发生错误判断的百分率。
通过混淆矩阵,可以获得分类器的正确识别率和错误识别率。
各模式正确识别率:$R_{i}=c m_{i i}, \quad i=1, \cdots, N$
平均正确识别率:$R_{A}=\sum_{i=1}^{N}\left(c m_{i i} \cdot T_{i}\right) / T_{0}$
各模式错误识别率:$W_{i}=\sum_{j=1, j \neq i}^{N} c m_{i j}=1-c m_{i i}=1-R_{i}$
平均错误识别率:$W_{A}=\sum_{i=1}^{N} \sum_{j=1, j \neq i}^{N}\left(c m_{i i} \cdot T_{i}\right) / T_{0}=1-R_{A}$
标签:idt matrix 综合 cte 平方根 预测算法 目标 有序 算法
原文地址:https://www.cnblogs.com/fangxiaoqi/p/11456301.html