标签:递归 函数 nbsp 常微分方程 img size font 原理 ima
用递推方法解递归方程,也就是我们常用的数学归纳法,用生成函数解递归方程,也就是我们使用循环代替递归。
这节,我们利用高等数学的常微分方程,来进行求解递归式。
K阶常系数线性齐次递归方程形如:
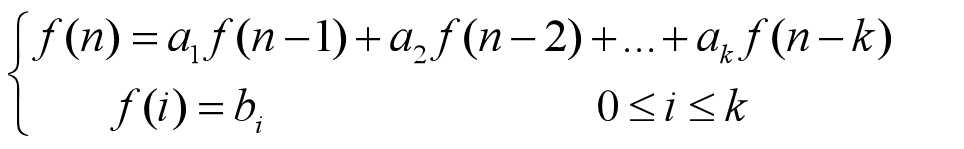
其中,bi为常数,第2项为方程初始条件。 在上式中,用xn取代f(n), 有:
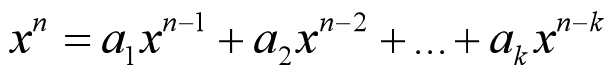
两边分别处以xn-k,得:
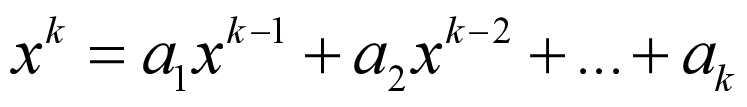
特征方程如下:
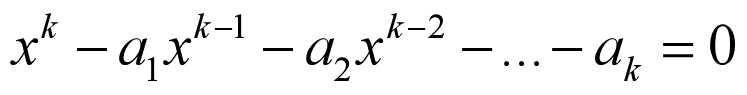
练习:
解下列递归方程:
1. f(n)=3f(n-1), f(0)=5
2. f(n)=2f(n-1) f(0)=2
3. f(n)=5f(n-1) – 6f(n-2), f(0)=1, f(1)=1
4. f(n)= -6f(n-1) – 9f(n-2), f(0)=3, f(1)=-3
5.求解斐波那契数列

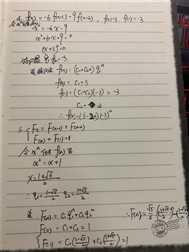
K阶常系数线性非齐次递归方程形如:
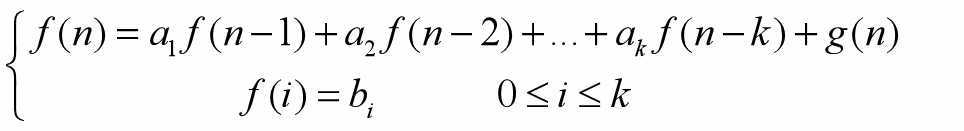
其中,bi为常数,第2项为方程初始条件。 它的通解形式为:
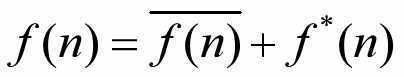
其中,
1) 为对应齐次递归方程的通解
2) f*(n) 为原非齐次递归方程的特解
解题原理:
1. 一般没有寻找特解的有效方法
2. 先根据g(n)具体形式,确定特解;再将特解代入递归方程,用待定系数法,求解特解的系数 3. g(n)分为以下几种情况 g(n)是n的m次的多项式 g(n)是n的指数函数

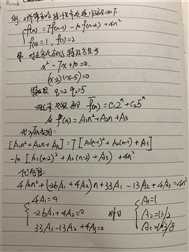
标签:递归 函数 nbsp 常微分方程 img size font 原理 ima
原文地址:https://www.cnblogs.com/littlepage/p/11470322.html