标签:ati mic ide family 分类 样本 概念 不能 类信息
C4.5属于决策树算法的分类树决策树更是常见的机器学习方法,可以帮助我们解决分类与回归两类问题。以决策树作为起点的原因很简单,因为它非常符合我们人类处理问题的方法,而且逻辑清晰,可解释性好。从婴儿到长者,我们每天都使用无数次!
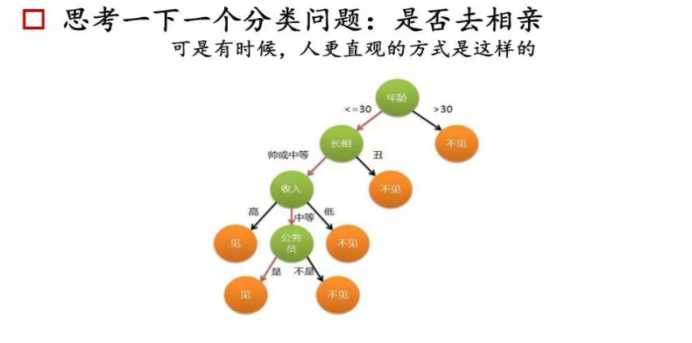
决策树的总体流程;
总体流程
分而治之(devide and conquer)
自根结点的递归过程
从每一个中间结点寻找一个划分(split and test)的属性
三种停止条件:
当前结点包含的样本属于同一类别,无需划分
当前属性集为空,或是所有样本在所有属性值上取值相同,无法划分
当前结点包含的样本集合为空,不能划分
核心数学概念:熵
信息熵(entropy)是度量样本集合“纯度”最常用的一种指标

C4.5算法流程
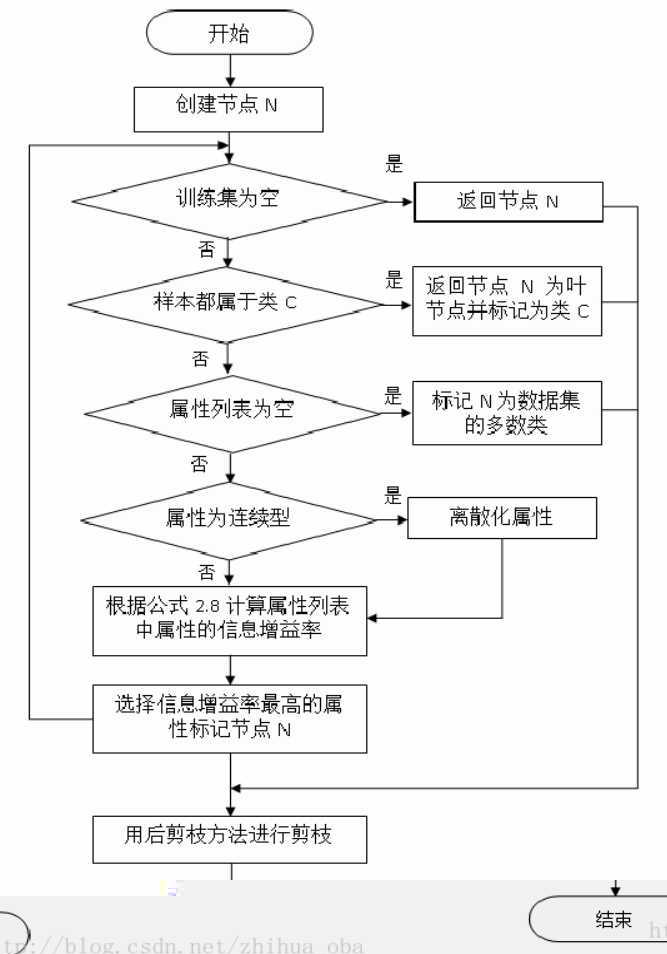
C4.5算法优缺点分析
优点:
(1)通过信息增益率选择分裂属性,克服了ID3算法中通过信息增益倾向于选择拥有多个属性值的属性作为分裂属性的不足;
(2)能够处理离散型和连续型的属性类型,即将连续型的属性进行离散化处理;
(3)构造决策树之后进行剪枝操作;
(4)能够处理具有缺失属性值的训练数据。
缺点:
(1)算法的计算效率较低,特别是针对含有连续属性值的训练样本时表现的尤为突出。
(2)算法在选择分裂属性时没有考虑到条件属性间的相关性,只计算数据集中每一个条件属性与决策属性之间的期望信息,有可能影响到属性选择的正确性。
算法详解:https://blog.csdn.net/zjsghww/article/details/51638126
算法程序
while(当前节点不纯)
1.计算当前节点的类别熵Info(D)(以类别取值计算)
2.计算当前节点的属性熵info(Ai)(按照当前属性取值下的类别取值计算)
3.计算各个属性的信息增益Gain(Ai) = Info(D)-info(Ai)
4.计算各个属性的分类信息度量H(Ai)(按照属性取值计算)
5.计算各个属性的信息增益率 IGR = Gain(Ai)/H(Ai)
and while
当前节点设置为叶子节点
标签:ati mic ide family 分类 样本 概念 不能 类信息
原文地址:https://www.cnblogs.com/normaltang/p/11484771.html