标签:结合 高斯 数学基础 取值 办公室 ati 表示 ace 离散
说到朴素贝叶斯算法,很自然地就会想到贝叶斯概率公式,这是我们在高中的时候就学过的只是,没错,这也真是朴素贝叶斯算法的核心,今天我们也从贝叶斯概率公式开始,全面撸一撸朴素贝叶斯算法。
定义1:完备事件组
${A_1} \cup {A_2} \cup \cdots \cup {A_n} = \Omega $,且${A_i} \cap {A_j} = \emptyset ,1 \le i \ne j \le n$,则称${A_1},{A_2}, \cdots ,{A_n}$为一个完备事件组。
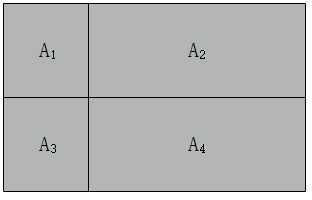
也就是说,如果${A_1},{A_2}, \cdots ,{A_n}$并集是完整的事件空间,且两两之间相互独立(不相交),那么${A_1},{A_2}, \cdots ,{A_n}$就是完备事件组。就像下图中的事件${A_1},{A_2},{A_3},{A_4}$,他们之间两两不相交,但合起来(并集)就构成了一个完整的大灰色矩形框(完整的事件空间):
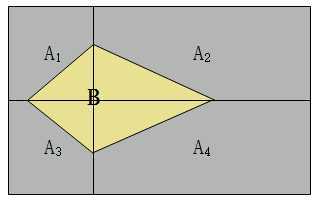
现在,如下图所示,有一个事件$B$,$B$事件只有在事件${A_i}$发生的基础上才会发生。注意,${A_i}$有可能是${A_1}$,也有可能是${A_2}$、${A_3}$、${A_4}$,而且${A_1}$、${A_2}$、${A_3}$、${A_4}$事件发生后发生$B$事件的概率可能不相等。
说到这里又有两个概念了:
先验概率:有简单统计分析可以获得的概率,例如$P({A_i})$
条件概率:在事件${A_i}$发生的前提下,发生事件B的概率,表示为$P(B|{A_i})$。
联合概率:事件${A_i}$和事件$B$同时发生的概率,表示为$P(B,{A_i})$。整个过程首先得保证${A_1}$发生,概率为$P({A_1})$,发生${A_1}$再发生$B$,概率是$P(B|{A_1})$,所以有:
由上面几个概念,就可以引申出全概率公式:
这就是$B$事件的全概率公式,意思是如果有某个事件$B$的发生总是以另一事件${A_i}$作为前提(原因),那么把各种前提事件${A_i}$下$B$发生的概率加起来就是事件$B$发生的概率。对上图中的例子就有:
$P(B) = P({A_1})P(B|{A_1}) + P({A_2})P(B|{A_2}) + P({A_3})P(B|{A_3}) + P({A_4})P(B|{A_4})$
从上面对全概率公式的介绍中我们知道了,事件$B$发生的概率就是在各个${A_i}$与事件$B$的联合概率之和,也就是在各种不同${A_i}$情况下发生$B$事件概率之和。现在,我们考虑另一种场景:已知事件$B$发生了,问是由事件${A_i}$导致的概率,也就是$B$发生前提下发生事件${A_i}$的条件概率,即$P({A_i}|B)$,怎么求呢?这就是贝叶斯概率公式解决的问题。
贝叶斯概率公式如下所示:
\[P({A_i}|B) = \frac{{P(B,{A_i})}}{{P(B)}}\]
也就是说,$B$发生前提下发生事件${A_i}$的条件概率等于事件${A_i}$、$B$的联合概率与事件$B$发生的概率之间的商。继续,我们将2.1节讲过的联合概率公式和全概率公式代入上面的贝叶斯概率公式,就得到了完整的贝叶斯公式:
\[P({A_i}|B) = \frac{{P(B,{A_i})}}{{P(B)}} = \frac{{P({A_i})P(B|{A_i})}}{{\sum\limits_1^n {P({A_i})P(B|{A_i})} }}\]
贝叶斯概率公式的作用:如果已知事件$B$发生了,去探求是某个原因${A_i}$导致这一结果发生的概率$P({A_i}|B)$,也就某个原因占所有原因的比例。
为了更加透彻理解贝叶斯概率公式,我们现在来分析一个例子:
病树的主人外出,委托邻居浇水,假设已知如果不浇水树死去的概率为$0.8$,若浇水,则树死去的概率为$0.15$,有$0.9$的把握确定邻居记得浇水。若主人回来时树已经死去,求邻居忘记浇水的概率?
我们用${A_1}$表示事件邻居记得浇水,${A_2}$表示事件邻居忘记浇水,用${B_1}$表示树活着,用${B_2}$表示树死了,那么,已知的概率有:
邻居记得浇水概率:$P({A_1}) = 0.9$
不浇水后树死去的条件概率:$P({B_2}|{A_2}) = 0.8$
浇水后树死去的条件概率:$P({B_2}|{A_1}) = 0.15$
邻居忘记浇水的概率:$P({A_2}=1 - P({A_1}) = 0.1$
那么,由全概率公式我们可以计算出树活着的概率:
$P({B_2}) = P({A_1})P({B_2}|{A_1}) + P({A_2})P({B_2}|{A_2}) = 0.9 \times 0.15 + 0.1 \times 0.8 = 0.215$
进而用贝叶斯概率公式计算树死去情况下邻居忘记浇水的概率:
$P({A_2}|{B_2}) = \frac{{P({A_2})P({B_2}|{A_2})}}{{P({B_2})}} = \frac{{0.1 \times 0.8}}{{0.215}} = 0.372$
我们通过一个例子来循序渐进地学习朴素贝叶斯算法。
假设办公室$6$成员工为程序员,$4$成为非程序员,程序员穿格子衬衫的概率是$0.7$,非程序员穿格子衬衫的概率是$0.1$,现在迎面走来一位穿格子衬衫的哥们,我们来判断一下这位是否是程序员?
用${A_1}$表示穿格子衬衫,${A_2}$表示不穿给支衬衫,${B_1}$表示是程序员,${B_2}$表示非程序员,有:
$P({B_1}) = 0.6$
$P({B_2}) = 0.4$
$P({A_1}|{B_1}) = 0.7$
$P({A_1}|{B_2}) = 0.1$
由贝叶斯概率公式可以计算那么穿格子衬衫的哥们是程序员和非程序员的概率分别是:
$P({B_1}|{A_1}) = \frac{{P({B_1})P({A_1}|{B_1})}}{{P({B_1})P({A_1}|{B_1}) + P({B_2})P({A_1}|{B_2})}} = \frac{{0.6 \times 0.7}}{{0.6 \times 0.7 + 0.4 \times 0.1}} = \frac{{0.42}}{{0.46}} \approx 0.91$
$P({B_2}|{A_1}) = \frac{{P({B_2})P({A_1}|{B_2})}}{{P({B_1})P({A_1}|{B_1}) + P({B_2})P({A_1}|{B_2})}} = \frac{{0.4 \times 0.1}}{{0.6 \times 0.7 + 0.4 \times 0.1}} = \frac{{0.04}}{{0.46}} \approx 0.09$
因为$P({B_1}|{A_1}) > P({B_2}|{A_1})$,所以,我们认为这位哥们是程序员。
对这位哥们是否是程序员进行分类的方法,就是朴素贝叶斯算法。我们来总结一下这个过程:
(1)又已有数据统计分析出一些先验概率和条件概率。就像上面的$P({B_1})$、$P({B_2})$、$P({A_1}|{B_1})$、$P({A_1}|{B_2})$。当然,这个例子中的这些概率是直接给出的,在真实应用中,这些概率需要通过统计分析得出。
(2)结合已知的先验概率和条件概率,通过贝叶斯概率公式计算属于各个分类的概率。在这一步骤中,有一个技巧,我们在回到上面计算两个概率$P({B_1}|{A_1}) $、$ P({B_2}|{A_1})$的过程,发现分母不同,但是分支都是一样的,因为都是计算穿格子衬衫的概率,所以,在实际算法应用中,我们只需要计算分子,然后比较大小即可。
(3)比较属于各个分类的概率,将数据划分到概率最大的分类中。
我想现在你已经对朴素贝叶斯算法有些感觉了,那么现在,我们系统的描述一下朴素贝叶斯算法,并将其扩展到更加一般化的多维情况。
假设存在包含$m$个特征,样本容量为$n$的数据集$D = \{ (x_1^{(1)},x_2^{(1)}, \cdots ,x_m^{(1)},{y_1}),(x_1^{(2)},x_2^{(2)}, \cdots ,x_m^{(2)},{y_2}), \cdots ,(x_1^{(n)},x_2^{(n)}, \cdots ,x_n^{(n)},{y_n})\} $,${y}$是分类标签,其取值${y_i} \in ({c_1},{c_2}, \cdots ,{c_K})$。
通过对数据集$D$的统计分析,我们可以获得每个类别的先验概率:
$P(Y = {c_k}),k = 1,2, \cdots ,K$
以及各分类条件下的不同特征的条件概率:
$P({X_j} = {x_j}|Y = {c_k})$ (在$ {c_k}$类中第$j$维特征取值为$ {x_j}$的概率)
朴素贝叶斯算法有一个前提假设,那就是各特征之间相互独立,对于不同特征组合下的条件概率有:
$P(X = x|Y = {C_k}) = P({X_1} = {x_1},{X_2} = {x_2}, \cdots ,{X_m} = {x_m}|Y = {C_k}) = \prod\limits_{j = 1}^m {P(} {X_j} = {x_j}|Y = {c_k})$
同时由全概率公式可得:
$P(X = x) = \sum\limits_{j = 1}^K {P(Y = {C_k}} )P({X_1} = {x_1},{X_2} = {x_2}, \cdots ,{X_m} = {x_m}|Y = {C_k}) = \sum\limits_{j = 1}^K {P(Y = {C_k}} )\prod\limits_{j = 1}^m {P(} {X_j} = {x_j}|Y = {c_k})$
当然,计算$P(X = x)$这一步其实是可以省略的,应该在贝叶斯概率公式中$P(X = x)$是作为分母,所有的$P(X = x)$都是一样的,只需要计算分子就可以了。
之后通过贝叶斯 概率公式计算不同特征组合下属于不同分类概率:
$P(Y = {C_k}|X = x) = \frac{{P(Y = {C_k})P(X = x|Y = {C_k})}}{{P(X = x)}}$
将之前获得的先验概率、条件概率、全概率公式都用上,代入到上式中:
$P(Y = {C_k}|X = x) = \frac{{P(Y = {C_k})\prod\limits_{j = 1}^m {P(} {X_j} = {x_j}|Y = {c_k})}}{{\sum\limits_{j = 1}^K {P(Y = {C_k}} )\prod\limits_{j = 1}^m {P(} {X_j} = {x_j}|Y = {c_k})}}$
最后比较属于各不同分类下的概率大小,取最大的一个分类概率,所以朴素贝叶斯分类算法可以表示为:
$P(Y = {C_k}|X = x) = \underbrace {argmax}_{{C_k}}\frac{{P(Y = {C_k})\prod\limits_{j = 1}^m {P(} {X_j} = {x_j}|Y = {c_k})}}{{\sum\limits_{j = 1}^K {P(Y = {C_k}} )\prod\limits_{j = 1}^m {P(} {X_j} = {x_j}|Y = {c_k})}}$
上面说过,计算各分类下概率时分母$P(X = x)$都一样,为节省计算量,可以分母,最终,朴素贝叶斯算法可以表示为:
$P(Y = {C_k}|X = x) = \underbrace {argmax}_{{C_k}}P(Y = {C_k})\prod\limits_{j = 1}^m {P(} {X_j} = {x_j}|Y = {c_k})$
这也是朴素贝叶斯分类算法的目标函数。
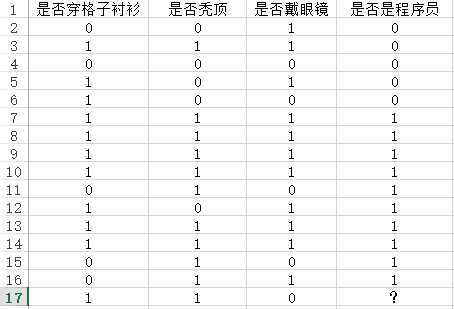
估计看了这么多数学表达,很多人都有些晕了,来,我们继续通过一个例子来解读。有如下所示的一个数据集(纯属杜撰),每个员工有三个特征属性——是否穿格子衬衫(${x_1}$)、是否秃顶(${x_2}$)、是否戴眼镜(${x_3}$),用来分类是否是程序员($y$),$1$表示肯定,$0$表示否定。现在要做的是对最后一条记录进行分类,即判断是否是程序员。
计算先验概率:
$P(y = 0) = \frac{5}{{15}} = \frac{1}{3}$
$P(y = 1) = \frac{{10}}{{15}} = \frac{2}{3}$
不同分类下各特征值的条件概率:
$P({x_1} = 0|y = 0) = \frac{3}{5},P({x_1} = 1|y = 0) = \frac{2}{5},P({x_1} = 0|y = 1) = \frac{2}{5},P({x_1} = 1|y = 1) = \frac{3}{5}$
$P({x_2} = 0|y = 0) = 1,P({x_2} = 1|y = 0) = 0,P({x_2} = 0|y = 1) = \frac{1}{{10}},P({x_2} = 1|y = 1) = \frac{9}{{10}}$
$P({x_3} = 0|y = 0) = \frac{3}{5},P({x_3} = 1|y = 0) = \frac{2}{5},P({x_3} = 0|y = 1) = \frac{1}{5},P({x_3} = 1|y = 1) = \frac{4}{5}$
通过贝叶斯概率公式计算最后一个样本属于不同分类的概率。
非程序员的概率:
$\eqalign{
& P(y = 0|{x_1} = 1,{x_2} = 0,{x_3} = 1) = \frac{{P(y = 0)P({x_1} = 1,{x_2} = 0,{x_3} = 1|y = 0)}}{{P({x_1} = 1,{x_2} = 0,{x_3} = 1)}} \cr
& = \frac{{\frac{1}{3} \times \frac{2}{5} \times 1 \times \frac{2}{5}}}{{\frac{1}{3} \times \frac{2}{5} \times 1 \times \frac{2}{5} + \frac{2}{3} \times \frac{3}{5} \times \frac{1}{{10}} \times \frac{4}{5}}} \approx 0.625 \cr} $
是程序员的概率:
$\eqalign{
& P(y = 1|{x_1} = 1,{x_2} = 0,{x_3} = 1) = \frac{{P(y = 1)P({x_1} = 1,{x_2} = 0,{x_3} = 1|y = 1)}}{{P({x_1} = 1,{x_2} = 0,{x_3} = 1)}} \cr
& = \frac{{\frac{2}{3} \times \frac{3}{5} \times \frac{1}{{10}} \times \frac{4}{5}}}{{\frac{1}{3} \times \frac{2}{5} \times 1 \times \frac{2}{5} + \frac{2}{3} \times \frac{3}{5} \times \frac{1}{{10}} \times \frac{4}{5}}} \approx 0.375 \cr} $
因为$P(y = 1|{x_1} = 1,{x_2} = 0,{x_3} = 1) \approx 0.625 > P(y = 0|{x_1} = 1,{x_2} = 0,{x_3} = 1) \approx 0.375$,该职工不是程序员的概率要大一些,所以判定该职工非程序员。
还是上面的预测是否是程序员的数据集,假设有如下所示的一条数据,然后预测是否是程序员:

还是按照上面的步骤进行计算,于是有:
$\eqalign{
& P(y = 0|{x_1} = 1,{x_2} = 1,{x_3} = 0) = \frac{{P(y = 0)P({x_1} = 1,{x_2} = 1,{x_3} = 0|y = 0)}}{{P({x_1} = 1,{x_2} = 1,{x_3} = 0)}} \cr
& = \frac{{\frac{1}{3} \times \frac{2}{5} \times 0 \times \frac{3}{5}}}{{\frac{1}{3} \times \frac{2}{5} \times 0 \times \frac{3}{5} + \frac{2}{3} \times \frac{3}{5} \times \frac{9}{{10}} \times \frac{0}{5}}} = 0 \cr} $
等于$0$。仔细一看就明白了因为在所有非程序员的分类中,没有一个秃顶的,即:
$P({x_2} = 1|y = 0) = 0$
所以造成贝叶斯概率公式计算式的分子是$0$。细细一想,这样的话,只要是秃顶的,无论是否是穿格子衬衫、是否戴眼镜,就一定是程序员。这样真的没问题吗?结合实际来想,秃顶的也可能是大领导啊,只是因为训练数据非程序员中没有秃顶的,就认为非程序员一定不秃顶显然不合适,而且也造成了是否穿衬衫、是否戴眼镜这两列信息没什么用了(信息丢失)。
这就是朴素贝叶斯算法的先天缺陷:其他属性携带的信息被训练集中未出现的属性值“抹去”,却预测出来的概率绝对为$0$。为了拟补这一缺陷,前辈们引入了拉普拉斯平滑的方法:对先验概率的分子(划分的计数)加$1$,分母加上类别数;对条件概率分子加$1$,分母加上对应特征的可能取值数量。这样在解决零概率问题的同时,也保证了概率和依然为$1$:
$P(c) = \frac{{|{D_c}|}}{{|D|}} \to P(c) = \frac{{|{D_c}| + 1}}{{|D| + N}}$
$P({x_i}|c) = \frac{{|{D_{{x_i}|c}}|}}{{|{D_c}|}} \to P({x_i}|c) = \frac{{|{D_{{x_i}|c}}| + 1}}{{|{D_c}| + {N_i}}}$
其中,$N$表示数据集中分类标签,${N_i}$表示第$i$个属性的取值类别数,${|D|}$样本容量,${|{D_c}|}$表示类别$c$的记录数量,${|{D_{{x_i}|c}}|}$表示类别$c$中第$i$个属性取值为${x_i}$的记录数量。
将这两个式子应用到上面的计算过程中,就可以弥补朴素贝叶斯算法的这一缺陷问题。
我们在上文中说到过的所有理论、案例都是围绕离散型属性来展开的,当属性为离散型时,先验概率和条件概率可以通过计算所在比例获得,但现实应用中的数据往往并不都是离散型属性也有可能是连续型,例如上面判断程序员的例子,在是否戴眼镜这一属性改为眼睛近视度数,这个近视度数就是连续型,其取值可以取值范围内的任意整数甚至浮点数。
当面对这种连续型的,又该怎么做呢?
有两种方法:
(1)通过划分区间的方式离散化。
这种方法思想是将特征属性的取值范围划分为若干个区间,从而将连续型属性离散化,例如眼睛近似度数是从0到1000度,那么我们可以划分为从0开始,区间长度为100的10个区间,这样就讲眼睛近视度数划分为10个离散类别,达到离散化的目的。
但是这种离散化的方法难以把握划分区间长度,如果划分区间太小,划分后的区间数量就会很多,每一个区间的记录数量很少,可能导致对条件概率$P(X = x|y)$误差不可靠。如果划分区间长度太长,就导致部分信息丢失,而且不同类别的记录也有很大可能划分到同一区间,导致分类不准确。
(2)通过概率密度函数计算概率。
这种方法首先需要假设该连续型属性的取值服从某种概率分布,然后通过训练数据做参数估计,获得分布函数,在计算概率时,根据密度函数来计算概率。
通常,在多数情况下,我们假设数据是服从高斯分布的,即$P({x_i}|c) \sim N({\mu _{c,i}},\sigma _{c,i}^2)$。其中,${\mu _{c,i}}$和$\sigma _{c,i}^2$分别是$c$类样本在第$i$个属性上取值的均值和方差,于是有:
$P({x_i}|c) = \frac{1}{{\sqrt {2\pi } {\sigma _{c,i}}}}{e^{ - \frac{{{{(x - {\mu _{c,i}})}^2}}}{{2\sigma _{c,i}^2}}}}$
最后,对朴素贝叶斯分类算法优缺点做一个总结。
优点:
(1)朴素贝叶斯分类算法根源于贝叶斯概率公式,有很好的数学基础,分类效率稳定。
(2)对小规模的数据表现很好,能个处理多分类任务,适合增量式训练,尤其是数据量超出内存时,我们可以一批批的去增量训练。
(3)对缺失数据不太敏感,算法也比较简单,常用于文本分类。
缺点:
(1)理论上,朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此,这是因为朴素贝叶斯模型给定输出类别的情况下,假设属性之间相互独立,这个假设在实际应用中往往是不成立的,在属性个数比较多或者属性之间相关性较大时,分类效果不好。而在属性相关性较小时,朴素贝叶斯性能最为良好。对于这一点,有半朴素贝叶斯之类的算法通过考虑部分关联性适度改进。
(2)需要知道先验概率,且先验概率很多时候取决于假设,假设的模型可以有很多种,因此在某些时候会由于假设的先验模型的原因导致预测效果不佳。
(3)由于我们是通过先验和数据来决定后验的概率从而决定分类,所以分类决策存在一定的错误率。
(4)对输入数据的表达形式很敏感。
参考:
https://www.cnblogs.com/pinard/p/6069267.html
https://www.jianshu.com/p/5953923f43f0
标签:结合 高斯 数学基础 取值 办公室 ati 表示 ace 离散
原文地址:https://www.cnblogs.com/chenhuabin/p/11508673.html