C++函数章节知识点浅析

标签：中介   多少   设计   asc   nec   自动调用   sort   好的   i++   

C++函数章节知识点浅析

一，为什么要用函数

1，可重用性：函数是定义好的，可重用的功能模块，可以方便在程序中多次调用。
2，使程序简洁明了：函数可以将一个比较复杂的程序系统的分为若干块简洁的模块，减少程序整体复杂性，便于分工合作和修改维护。
例如，求x的平方加y的平方的值：

#include<iostream>
using namespace std;
double fun(double x)//定义一个求平方的函数
{
    return x * x;
}
int main()
{
    double x, y,re;
    cin >> x >> y;
    re = fun(x) + fun(y);//分别调用fun()函数，再实现求和
    cout << re << endl;
    return 0;
}

二，为什么要用函数重载

1，C++允许功能相近的函数在相同的作用域内以相同函数名声明，从而形成重载。方便使用，便于记忆。

当参数类型变多时，如果不使用重载函数，就会使函数名变多，调用时要找到相应的函数名，十分繁琐，下面举例：

//当参数类型变化时，需要重新定义不同名字的函数，使得声明函数和调用函数变得麻烦
int add1(int x,int y);
float add2(foat x,float y);
double add3(doublex,double y);

利用重载函数实现上面功能：

//形参类型不同，定义相同名字函数，实现重载函数功能，调用时系统会自动调用相应参数类型的函数
int add(int x,int y);
float add(float x,float y);
double add(double x,double y);

三，什么是值传递

值传递是指在调用函数时将实际参数复制一份传递到函数中，这样在函数中如果对参数进行修改，将不会影响到实际参数
举例说明（超级经典的例子，哈哈）：

#include<iostream>
using namespace std;
void swap(int a, int b)
{
    int t = a;
    a = b;
    b = t;
}
int main()
{
    int x = 5,y=10;
    cout << "x=" << x << "   y=" << y << endl;
    swap(x, y);
    cout << "x=" << x << "   y=" << y << endl;
    return 0;
}

输出结果：

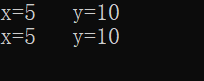
结果分析：
swap函数由于是值传递，其实并没有将主函数中的两个值交换，因为实参传递给形参时，形参重新开辟了一个存储空间，储存和实参相同的值，swap函数中操作的其实是形参的值，并不会影响实参。

四，什么是地址传递

地址传递是指当调用一个过程时，是把实参变量的内存地址传递给被调用过程的形参，也就是说形参与实参使用相同地址的内存单元。因此当在被调用过程中改变形参的值，就等于改变了实参的值。
举例：（只需要把上面swap函数稍微改一下就可以实现交换功能啦！）

void swap(int *a, int *b)//通过地址传递
{
    int t = *a;
    *a = *b;
    *b = t;
}

输出结果：

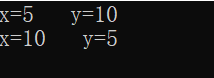
结果分析：
通过地址传递，形参与实参使用相同地址的内存单元。对形参的操作其实就是对实参的操作，因此当在被调用过程中改变形参的值，就等于改变了实参的值

地址传递的特性：
1，形参与实参使用相同地址的内存单元。因此当在被调用过程中改变形参的值，就等于改变了实参的值。
2，可以节省形实结合时多余的内存开销，因为只需要传给实参一个地址就行了，来看一个例子吧：

#include<iostream>
using namespace std;
void sort(int *a)//通过地址传递
{
    int t;
    for(int i=0;i<9;i++)
        for (int j = 0; j < 10; j++)
        {
            if (*(a + j) < *(a + j + 1))
            {
                t = *(a + j);
                *(a + j) = *(a + j + 1);
                *(a + j + 1) = t;
            }
        }
}

int main()
{
    int a[10] = { 3,0,4,5,6,9,14,1,12,7 };
    sort(a);
    for (int i = 0; i < 10; i++)
        cout << a[i] << " ";
    return 0;
}

通过地址传递，只需将数组首地址传递给形参，就可以进行排序，这样大大节省了内存开支。

五，设计实验和教案，分析如何编写递归函数

定义：函数直接或间接地调用自身，称为递归调用。
举例，求4！的值是多少？：

编写递归函数两大关键：
1，把问题分解为小部分，使其能够调用自身函数
可以这样分解：

2，确保最终分解出来的问题，是一个已知解的问题，即设置出口函数。

例子一：
求n!的值。

unsigned fac(unsigned n)
{
unsigned f;
if(n==0)//关键！设置出口
f=1;
else 
f=fac(n-1)*n;//调用自身
return f;
}

例子二（（难度较大））：

汉诺塔问题：
分析：有三根针A，B，C，将n个盘子从A针上移到C针上可以分解为下面三个步骤
1，将A中上n-1个盘子移到B针上（借助C针）：这是一个递归过程，无需考虑细节
2，把A针上剩下的一个盘子移到C针上：可以直接做到，递归出口
3，将B针上的n-1盘子移到C针上（借助A针）：这是一个递归过程，无需考虑细节

用hanoi函数实现1，3过程，move函数实现2过程

void move(char src, char dest)
{
    cout << src << "-->" << dest << endl;
}
//把n个盘子从src针移动到dest针，以medium针作为中介
void hanoi(int n, char src, char medium, char dest)
{
    if (n == 1)//递归出口
        move(src, dest);
    else
    {
        hanoi(n - 1, src, dest, medium);
        move(src, dest);
        hanoi(n - 1, medium, src, dest);
    }
}

C++函数章节知识点浅析

标签：中介   多少   设计   asc   nec   自动调用   sort   好的   i++   

原文地址：https://www.cnblogs.com/-believe-me/p/11519054.html