算法设计与分析——矩阵连乘问题

标签：strong   bsp   算法   oid   复杂   int   http   算法设计   计算   

问题描述：

给定n个矩阵｛A1,A2,…,An｝，其中Ai与Ai+1是可乘的，i=1，2…，n-1。如何确定计算矩阵连乘积的计算次序，使得依此次序计算矩阵连乘积需要的数乘次数最少。例如，给定三个连乘矩阵{A1，A2，A3}的维数分别是10*100，100*5和5*50，采用（A1A2）A3，乘法次数为10*100*5+10*5*50=7500次，而采用A1（A2A3），乘法次数为100*5*50+10*100*50=75000次乘法，显然，最好的次序是（A1A2)A3，乘法次数为7500次。

加括号的方式对计算量有很大的影响，于是自然地提出矩阵连乘的最优计算次序问题，即对于给定的相继n个矩阵，如何确定矩阵连乘的计算次序，使得依此次序计算矩阵连乘积需要的数乘次数最少。

问题分析：

 矩阵连乘也是Catalan数的一个常用的例子，关于时间复杂度的推算需要参考离散数学关于Catalan的内容。

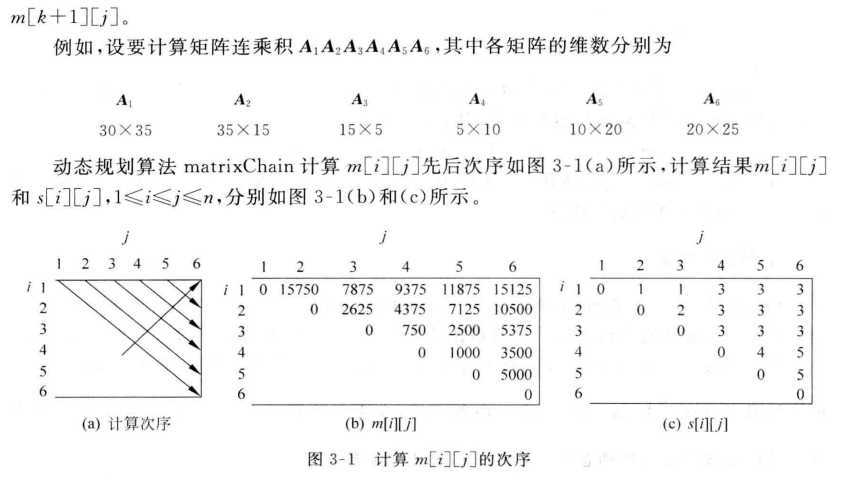
下面考虑使用动态规划法解矩阵连乘积的最优计算次序问题。

1、分析最优解的结构

 问题的最优子结构性质是该问题可以用动态规划求解的显著特征！！！

2、建立递归关系

 3、计算最优值

public static void matrixChain(int n) {
    for (int i = 1; i <= n; i++) {
        m[i][i] = 0;
    }
    for (int r = 2; r <= n; r++) {//i与j的差值
        for (int i = 1; i <= n - r + 1; i++) {
            int j = i + r - 1;
            m[i][j] = m[i + 1][j] + p[i - 1] * p[i] * p[j];
            s[i][j] = i;
            for (int k = i + 1; k < j; k++) {
                int t = m[i][k] + m[k + 1][j] + p[i - 1] * p[k] * p[j];
                if (t < m[i][j]) {
                    m[i][j] = t;
                    s[i][j] = k;
                }
            }
        }
    }
}

算法设计与分析——矩阵连乘问题

标签：strong   bsp   算法   oid   复杂   int   http   算法设计   计算   

原文地址：https://www.cnblogs.com/wkfvawl/p/11564275.html