标签：过程   fine   cout   算法   前缀   alt   单源最短路径   数据结构   归并   

一 哈夫曼树

1.1 基本概念

• 算法思想
  • 贪心算法（以局部最优，谋求全局最优）
    • 示例
      • 【树论：最优（二叉）数=带权路径最短的树】
        • 哈夫曼（树）编码
      • 【图论：最小（代价）生成树】
        • 普里姆算法（Prim）（加点法，归并点）
        • 克鲁斯卡尔（Kruskal）算法（加边法，归并边）
      • 【图论：单源最短路径=从某一结点出发至其他结点的带权路径之和最小 / 多源最短路径=某一对结点之间的带权路径之和最小】
        • 迪杰斯特拉算法（Dijskra）
• 定义
  • 哈夫曼树 = 最优((满)二叉)树 = 带权路径之和最短的树
  • 哈夫曼树所产生的哈夫曼编码 = (最优)前缀编码

1.2 算法描述/构造过程

1.3 算法实现

• 1> 定义存储结构

# define MAXNEGATIVE -9999 //最大负值 
# define MAXPOSITIVE  9999 //最大正值 

typedef struct HuffmanNode{ // 加 typedef : 避免发生编译错误 " variable or field 'functionName' declared void "
    double weight;
    int parent, lchild, rchild; //当前节点的双亲结点、左右孩子结点 
}*HuffmanTree;

• 2> 确定最小的两个结点的选择策略（贪婪策略）【次核心】

/**
 * 选择权值结点最小的两个结点 s1、s2 
 */
void Select(HuffmanTree &HT,int k,int *s1,int *s2){ 
    int min[2]={0, 0}; // 升序排名， 保留 HT中 权重值最小的两个结点的下标 
    cout<<"Select k:"<<k<<endl;
    HT[0].weight = MAXPOSITIVE; // 初始化为最大正值，方便被 初始结点比最小而比下去 
    for(int i=1;i<=k;i++){
//      cout<<"i:"<<i<<"\tweight:"<<HT[i].weight<<"\tparent:"<<HT[i].parent<<"\tparent.weight:"<<HT[HT[i].parent].weight<<endl;
        if( HT[i].parent==0 && (HT[i].weight<HT[min[1]].weight)){
            if(HT[i].weight<HT[min[0]].weight){ // 小于 最小者 
                min[1] = min[0]; min[0] = i; cout<<i<<"小于最小者！"<<endl;
            } else {
                min[1] = i;cout<<i<<"小于次小者！"<<endl;  //仅小于 次小者 
            }
        }
    } 
    *s1 = min[0]; // 最小者下标
    *s2 = min[1]; // 次小者下标 
//  cout<<"s1:"<<*s1<<"\ts2:"<<*s2<<endl; 
}

• 3> 创建 Huffman 树【核心】

/**
 * 创建 Huffman 树
 *   n : 初试结点（待编码结点）数 
 */
void CreateHuffmanTree(HuffmanTree &HT, int n){
    int m = 2*n-1;
    HT = new HuffmanNode[m+1]; // 0 位空余
    cout<<"Please input initiative node's weight : "<<endl; // 输入结点数据
    for(int i=1;i<=n;i++){
        cin>>HT[i].weight;
    }
    for(int k=1;k<=m;k++){ // 初始化所有结点 
        HT[k].lchild = 0;
        HT[k].rchild = 0;
        HT[k].parent = 0;
    }
    for(int j=n+1;j<=m;j++){
        int s1,s2;
        Select(HT, j-1, &s1, &s2); // 选择权值结点最小的两个结点s1、s2 
        HT[s1].parent = j; // 合并左右结点 
        HT[s2].parent = j; 
        HT[j].lchild = s1;
        HT[j].rchild = s2;
        HT[j].weight = HT[s1].weight + HT[s2].weight;
    }
}

• 4> 输出哈夫曼树

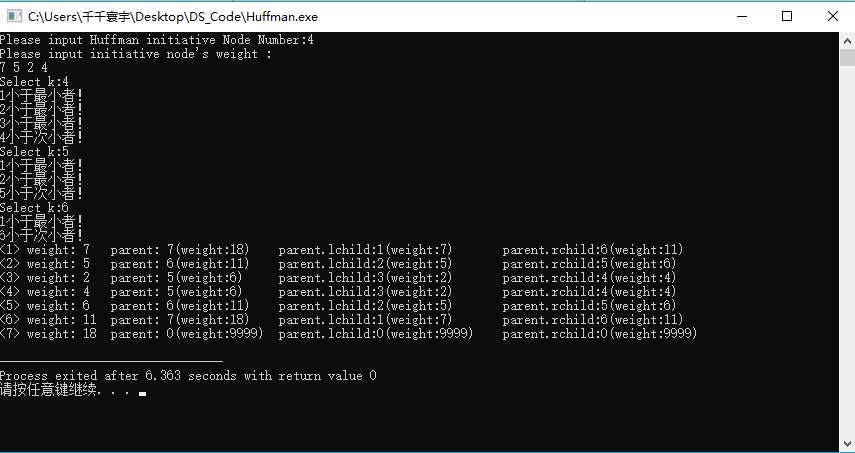
void OutputHuffmanTree(HuffmanTree &HT, int n){ // 输出 哈夫曼树 中 结点情况 
    int m = 2*n-1;
    for(int i=1;i<=m;i++){
        cout<<"<"<<i<<"> weight: "<<HT[i].weight<<"\t"<<"parent: "<<HT[i].parent<<"(weight:"<<HT[HT[i].parent].weight<<")\t";
        cout<<"parent.lchild:"<<HT[HT[i].parent].lchild<<"(weight:"<<HT[HT[HT[i].parent].lchild].weight<<")"<<"\t";
        cout<<"parent.rchild:"<<HT[HT[i].parent].rchild<<"(weight:"<<HT[HT[HT[i].parent].rchild].weight<<")"<<endl;
    }
}

• 5> 执行：Main函数

int main(){
    HuffmanTree HT;
    int n;
    cout<<"Please input Huffman initiative Node Number:"; // 输入哈夫曼结点初始结点数目 n
    int s1, s2;
    cin>>n; 
    CreateHuffmanTree(HT, n);
    OutputHuffmanTree(HT, n);
    return 0;
}

二 哈夫曼编码

三 哈夫曼译(解)码

四 参考文献

• 《数据结构(C语言版)：严蔚敏/吴伟民》

[C++] 数据结构之哈夫曼树(最优满二叉树) / 哈夫曼编码

标签：过程   fine   cout   算法   前缀   alt   单源最短路径   数据结构   归并   

原文地址：https://www.cnblogs.com/johnnyzen/p/11589415.html