迪杰斯特拉算法

标签：print   algorithm   private   system   数组   alt   i++   开始   fill   

问题描述

看一个应用场景和问题：

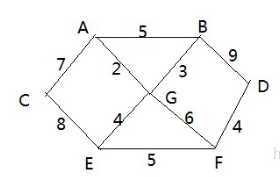
战争时期，胜利乡有7个村庄(A, B, C, D, E, F, G) ，现在有六个邮差，从G点出发，需要分别把邮件分别送到 A, B, C , D, E, F 六个村庄
各个村庄的距离用边线表示(权) ，比如 A – B 距离 5公里
问：如何计算出G村庄到 其它各个村庄的最短距离?
如果从其它点出发到各个点的最短距离又是多少?

代码实现

    /**
     * 存放顶点的数组
     */
    private String[] data;
    /**
     * 保存，从各个顶点出发到其它顶点的距离
     */
    private int[][] dis;
    /**
     * 保存到达目标顶点的前驱顶点
     */
    private int[][] pre;

    public FloydAlgorithm(String[] data, int[][] dis) {
        this.data = data;
        this.dis = dis;
        this.pre = new int[data.length][data.length];
        for (int i = 0; i < pre.length; i++) {
            Arrays.fill(pre[i], i);
        }
    }


    public void floydAlgorithm() {
        int len = 0;
        // 1. 对中间顶点遍历， k就是中间顶点的下标
        for (int k = 0; k < dis.length; k++) {
            // 2. 从i顶点开始出发
            for (int i = 0; i < dis.length; i++) {
                // 3. 到达j顶点
                for (int j = 0; j < dis.length; j++) {
                    len = dis[i][k] + dis[k][j];
                    if (len < dis[i][j]) {
                        dis[i][j] = len;
                        pre[i][j] = k;
                    }
                }
            }
        }
    }

    public void show(){
        for (int i = 0; i < dis.length; i++) {
            for (int j = 0; j < dis[i].length; j++) {
                System.out.print(data[i]+"==>"+data[j]+"最短路径为："+dis[i][j]+"\t");
            }
            System.out.println();
        }
    }


    public static void main(String[] args) {
        // 测试看看图是否创建成功
        String[] data = {"A", "B", "C", "D", "E", "F", "G"};
        //创建邻接矩阵
        int[][] matrix = new int[data.length][data.length];
        final int N = 65535;
        matrix[0] = new int[]{0, 5, 7, N, N, N, 2};
        matrix[1] = new int[]{5, 0, N, 9, N, N, 3};
        matrix[2] = new int[]{7, N, 0, N, 8, N, N};
        matrix[3] = new int[]{N, 9, N, 0, N, 4, N};
        matrix[4] = new int[]{N, N, 8, N, 0, 5, 4};
        matrix[5] = new int[]{N, N, N, 4, 5, 0, 6};
        matrix[6] = new int[]{2, 3, N, N, 4, 6, 0};
        FloydAlgorithm floydAlgorithm = new FloydAlgorithm(data, matrix);
        floydAlgorithm.floydAlgorithm();
        floydAlgorithm.show();
    }

迪杰斯特拉算法

标签：print   algorithm   private   system   数组   alt   i++   开始   fill   

原文地址：https://www.cnblogs.com/MND1024/p/11611593.html