标签:通过 独立 返回 坐标 mic 线性模型 离散 坐标下降 分布
参数:
fit_intercept : 布尔值
是否计算此模型的截距。 如果设置为false,则计算中不会使用截距(例如,如果数据已居中)。
verbose : 布尔值或整数可选
设置详细度
max_iter:整数,可选
要执行的最大迭代次数。
normalize:布尔值,可选,默认为True
当fit_intercept设置为False时,该参数将被忽略。 如果为真,则回归前的回归量X将通过减去平均值并除以l2-范数而归一化。
如果您自己想要标准化,请在调用fit到一个带有normalize=False估计器之前使用sklearn.preprocessing.StandardScaler。
precompute : True | False | ‘auto’
是否使用预先计算的Gram矩阵来加速计算。
cv:int,交叉验证生成器或迭代器,可选的
确定交叉验证拆分策略。 cv可能的输入是:
a)None,使用默认的3折交叉验证,
b)Integer,以指定折叠的数量。
c)一个要用作交叉验证生成器的对象。
d)一个迭代生产的训练/测试分割。
对于整数/无输入,使用KFold。
eps:float,可选 Cholesky对角线因子计算中的机器精度正则化。 对于有很严重病态的系统增加这个。(修正值)
positive : boolean (default=False)
将系数限制为> = 0。此种情况下,对于小α值,模型系数不收敛于普通最小二乘解。
仅仅达到由逐步的Lars-Lasso算法确定的α值中的最小值的系数通常与坐标下降Lasso估计的解相一致。
因此,使用LassoLarsCV只适用于期望并得到或者得到稀疏解(系数分布离散度大)的问题。
属性:
coef_:数组,形状(n_features,)
参数矢量
intercept_:浮点
决策函数的独立项。
coef_path_:数组,形状(n_features,n_alphas)
沿着路径的系数的变化值
alpha_:float
被估计的正则参数α
alphas_:数组,形状(n_alphas,)
沿着路径的不同α值
cv_alphas_:数组,形状(n_cv_alphas,)
沿着不同折路径的所有alpha值
n_iter_:类似数组或int
利用最佳alpha值通过Lars算法运行的迭代次数。
方法:
fit(X,y)使用X,y作为训练数据来拟合模型。
get_params([deep])获取此估算器的参数。
Predict(X)使用线性模型进行预测
score(X,y [,sample_weight])返回预测的决定系数R ^ 2。
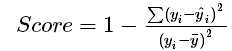
其中分别为真实值、真实值均值和预测值。
set_params(** params)设置此估算器的参数。
标签:通过 独立 返回 坐标 mic 线性模型 离散 坐标下降 分布
原文地址:https://www.cnblogs.com/dinol/p/11615997.html