标签:算法 处理 get tps 透明度 描述 图案 log 结束
区域:指已经表示成点阵形式的填充图形,是象素的集合。
区域填充:将区域内的一点(常称【种子点】)赋予给定颜色,然后将这种颜色扩展到整个区域内的过程。
区域填充算法要求区域是连通的,因为只有在连通区域中,才可能将种子点的颜色扩展到区域内的其它点。

1)内点表示:枚举出区域内部的所有象素,内部所有象素着同一个颜色,边界像素着与内部象素不同的颜色。
2)边界表示:枚举出区域外部的所有象素,边界上的所有象素着同一个颜色,内部像素着与边界象素不同的颜色。
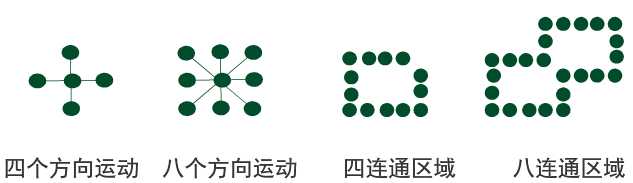
1)四向连通区域:从区域上一点出发可通过【上、下、左、右】四个方向移动的组合,在不越出区域的前提下,到达区域内的任意象素。
2)八向连通区域:从区域上一点出发可通过【上、下、左、右、左上、右上、左下、右下】八个方向移动的组合,在不越出区域的前提下,到达区域内的任意象素。
给定区域G一种子点(x, y),首先判断该点是否是区域内的一点,如果是,则将该点填充为新的颜色,然后将该点周围的四个点(四连通)或八个点(八连通)作为新的种子点进行同样的处理,通过这种扩散完成对整个区域的填充。
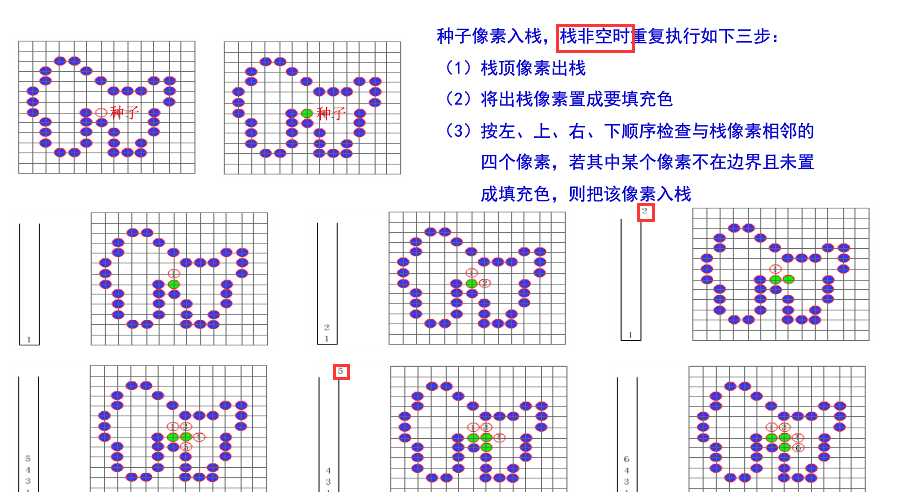
这里给出一个四连通的种子填充算法(区域填充递归算法),使用【栈结构】来实现
原理算法原理如下:种子像素入栈,当【栈非空】时重复如下三步:
这里给出八连通的种子填充算法的代码:
void flood_fill_8(int[] pixels, int x, int y, int old_color, int new_color)
{
if(x<w&&x>0&&y<h&&y>0)
{
if (pixels[y*w+x]==old_color)
{
pixels[y*w+x]== new_color);
flood_fill_8(pixels, x,y+1,old_color,new_color);
flood_fill_8(pixels, x,y-1,old_color,new_color);
flood_fill_8(pixels, x-1,y,old_color,new_color);
flood_fill_8(pixels, x+1,y,old_color,new_color);
flood_fill_8(pixels, x+1,y+1,old_color,new_color);
flood_fill_8(pixels, x+1,y-1,old_color,new_color);
flood_fill_8(pixels, x-1,y+1,old_color,new_color);
flood_fill_8(pixels, x-1,y-1,old_color,new_color);
}
}
}
a)有些像素会多次入栈,降低算法效率,栈结构占空间
b)递归执行,算法简单,但效率不高,区域内每一像素都要进/出栈,费时费内存
c)改进算法,减少递归次数,提高效率
从给定的种子点开始,填充当前扫描线上种子点所在的一区段,然后确定与这一段相邻的上下两条扫描线上位于区域内的区段(需要填充的区间),从这些区间上各取一个种子点依次把它们存起来,作为下次填充的种子点。反复进行这过程,直到所保存的各区段都填充完毕。
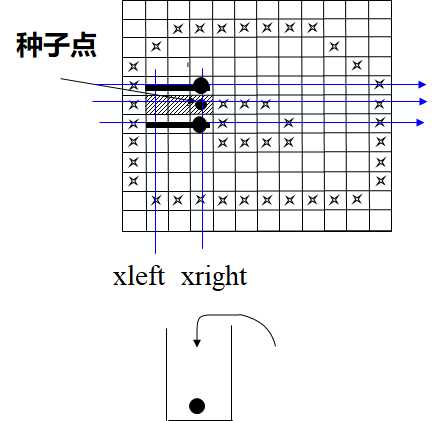
步骤 1:(初始化)将算法设置的堆栈置为空。将给定的种子点(x, y)压入堆栈
步骤 2:(出栈)如果堆栈为空,算法结束;否则取栈顶元素(x, y)作为种子点
步骤 3:(区段填充)从种子点(x, y)开始,沿纵坐标为y的当前扫描线向左右两个方向逐个像素用新的颜色值进行填充,直到边界为止即象素颜色等于边界色。设区间两边界的横坐标分别为xleft 和xright。
步骤4:在与当前扫描线相邻的上下两条扫描线上,以区间[xleft, xright]为搜索范围,求出需要填充的各小区间,把各小区间中最右边的点并作为种子点压入堆栈,转到步骤2。
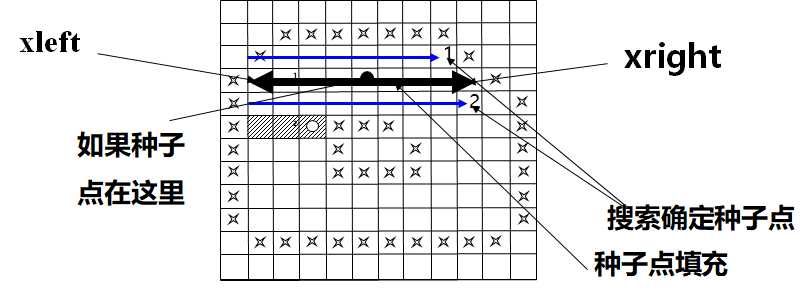
1)搜索原则:
从前一个填充的区间(边界之间的范围xleft, xright)作为后一条扫描线种子点寻找的范围。
2)填充原则:
从种子点往左,右填,填到边界
上述算法的描述过于抽象,直接看演示

Stack stack=new Stack();//堆栈 pixel_stack初始化
Stack.push (point); //(x,y)是给定的种子像素
while (!stack.empty())
{
p=(Point)(stack.pop());//出栈,从堆栈中取一像素作种子像素
x=p.x;
y=p.y;
savex=x;//保存种子点的横坐标x的值
while (pixels [y*w+x]!= boundary_color)
{
pixels [y*w+x]= new_color;
x++;
} //从种子像素开始向右填充到边界
xright=x–1; //保存线段的右端点
x=savex–1; //设定种子点往左填充的起点
while (pixels [y*w+x]!= boundary_color)
{
pixels [y*w+x] = new_color;
x=x–1;
}
//从种子像素开始向左填充到边界,以上两步完成区间填充。
xleft=x+1; //保存线段的左端点,加1是因为前面 循环时多减一次
x=xleft; //起点是上次的左端点
y=y+1; //开始处理上一条扫描线
while(x<=xright) //在上一条扫描线上检查是否需要填充
{
span_need_fill=false; //先设定为不需要填充
while (pixels [y*w+x] ==old_color&&x<=xright )
{
//待填充的线段
span_need_fill=true; //发现有旧象素,需要填充
x=x+1;
} //待填充的线段处理完,即遇到边界色,!=old_color跳出
if (span_need_fill) //如果区间需要填充,则将其右端点作为种子点压进堆栈
{
p=new Point(x-1,y);
stack.push (p); //进栈
span_need_fill=false;
}
//继续向右检查以防有遗漏
while (pixels [y*w+x] !=old_color &&x<=xright )
x=x+1;
} //在上一条扫描线上检查完
x=xleft;
y=y–2; //形成下一条扫描线的y值
//在下一条扫描线上从左向右检查位于区间[xleft,xright]上的像素,其方法与在上一条扫描线上检查的情况完全一样,见书。
}//出栈完
上一篇博客讲述了多边形的扫描转换 ,这里将多边形扫描转换和区域填充算法进行比较总结。
多边形扫描转换是指将多边形的顶点表示转化为点阵表示
区域填充只改变填充颜色,不改变区域表示方式
在区域填充算法中,要求给定区域内的一点作为种子点,然后从这一点根据连通性将新的颜色扩展到整个区域。
扫描转换多边形是从多边形的边界(顶点)信息出发,利用多种形式的连贯性进行填充的。
扫描转换区域填充的核心是知道多边形的边界,要得到多边形内部的像素集,有很多种办法。其中扫描线算法是利用一套特殊的数据结构,避免求交,然后一条条扫描线确定。
区域填充条件更强一些,不但要知道边界,而且要知道区域内的一点,可以利用四连通或八连通区域不断向外扩展。
填充一个定义的区域的选择包括:
a)选择实区域颜色或图案填充方式
b)选择某种颜色和图案
这些填充选择可以应用于多边形区域或用曲线边界定义的区域;此外,区域可用多种画笔、颜色和透明度参数来绘制
标签:算法 处理 get tps 透明度 描述 图案 log 结束
原文地址:https://www.cnblogs.com/wkfvawl/p/11625712.html