标签:The 合并 merge blog 副本 二叉树 github radix for
排序算法可以分为内部排序和外部排序,内部排序是数据记录在内存中进行排序,而外部排序是因排序的数据很大,一次不能容纳全部的排序记录,在排序过程中需要访问外存。
常见的内部排序算法有:冒泡排序、选择排序、插入排序、希尔排序、堆排序、快速排序、归并排序、基数排序等。
前面三种是简单排序,后续算法是在前面基础上进行优化。本文将基于C语言,依次介绍上述八大排序算法。
主要思想:依次对两个数比较大小,较大的数冒起来,较小的数压下来。
形象理解:一队新兵N个人整齐站成一列,教官想让他们按照身高排好队,看起来更协调,于是从前走到后走一趟,每次遇到相邻的两个人身高不协调时,就让两人互换位置。当走完一趟时,个子最高的人就被排到了最后。教官回到前排后发现队伍仍然不协调,于是又按照原样走了一趟。这样循环走了N-1趟之后,教官终于满意了。(注意:每次走一趟时,之前排到后面的高个子就不参与这次排序了;有时候可能还没走完N-1趟,教官就发现队伍已经协调了,于是排序结束。)
特点:简单易懂,排序稳定,但速度慢。
主要思想:针对冒泡排序,有一个地方可以优化,即在跑一趟的过程中,没必要两两交换,可以先记下最小值,跑完一趟后直接将最小值换到前面。
特点:比冒泡更快一些,但代价是跳跃性交换,排序不稳定。
完整代码
#include <stdio.h>
#include <stdlib.h>
void Swap_Two(int *p1, int *p2); //交换两个整数
void Select_Sort(int A[], int N); //选择排序
//主函数,其余类似
int main()
{
int N, i;
int *p = NULL;
//将N个整数存储至数组中
scanf("%d", &N); //读入个数N
p = (int *)malloc(sizeof(int) * N); //申请数组
for(i=0; i<N; i++){
scanf("%d", &p[i]);
}
//排序并打印
Select_Sort(p, N);
for(i=0; i<N; i++){
printf("%d", p[i]);
if(i != N-1)
printf(" ");
}
free(p);
return 0;
}
void Swap_Two(int *p1, int *p2){ //交换两个长整型数
int temp;
temp = *p1;
*p1 = *p2;
*p2 = temp;
return;
}
void Select_Sort(int A[], int N){ //选择排序
int i, j, min_idx;
for(i=0; i<N-1; i++){
min_idx = i; //初始化最小值索引
for(j=i+1; j<N; j++){
if(A[j] < A[min_idx]) //若待排序列中有比当前最小值还小的,则更新最小值索引
min_idx = j;
}
if(min_idx != i) //若更新过最小值索引
Swap_Two(&A[i], &A[min_idx]);
}
return;
}
主要思想:过程跟拿牌一样,依次拿N张牌,每次拿到到牌后,从后往前看,遇到合适位置就插进去。最终手上的牌从小到大。
特点:当数据规模较小或者数据基本有序时,效率较高。
完整代码
void Swap_Two(int *p1, int *p2){ //交换两个整数
int temp;
temp = *p1;
*p1 = *p2;
*p2 = temp;
return;
}
void Insert_Sort(int A[], int N){ //直插排序
int temp, i, k;
for(i=1; i<N; i++){
temp = A[i];
for(k=i-1; k>=0 && temp<A[k]; k--){
A[k+1] = A[k];
}
A[k+1] = temp;
}
return;
}
主要思想:设增量序列个数为k,则进行k轮排序。每一轮中,按照某个增量将数据分割成较小的若干组,每一组内部进行插入排序;各组排序完毕后,减小增量,进行下一轮的内部排序。
特点:针对插入排序的改进,当数据规模较大或无序时也比较高效。精妙之处在于,可以同时构造出两个特殊的有利条件(数据量小,基本有序),一个有利条件弱时,另外一个有利条件就强。(刚开始时虽然每组有序度低,但其数据量小;随着每轮的增量逐渐压缩,虽然各组数据量逐渐变大,但其有序度逐渐增加。)
完整代码
void Shell_Sort(int A[], int N){ //希尔排序
int k, i, j, p, temp;
int t = 0;
int D[33]; //假定增量序列不超过2^32
//定义Hibbard增量序列
for(k=1; k<33; k++){
t = 2 * t + 1; //增量序列项
if(t < N){
D[k] = t;
}else{
break;
}
}
//进行k-1(增量序列的个数)趟插排
for(p=k-1; p>=1; p--){
for(i=D[p]; i<N; i++){
temp = A[i];
for(j=i-D[p]; j>=0 && temp<A[j]; j-=D[p]){
A[j+D[p]] = A[j];
}
A[j+D[p]] = temp;
}
}
return;
}主要思想:将待排数组构建成一个最大堆,将堆顶最大元素换到后面,然后堆容量减1;类似进行N-1次操作即可。
主要思想:分治思想。选一基准元素,依次将剩余元素中小于该基准元素的值放置其左侧,大于等于该基准元素的值放置其右侧;然后,取基准元素的前半部分和后半部分分别进行同样的处理;以此类推,直至各子序列剩余一个元素时,即排序完成。
注意:对于小规模数据(n<100),快排由于用了递归,其效率可能还不如插排。因此通常可以定义一个阈值,当递归的数据量很小时停止递归,直接调用插排。
主要思想:类似两个有序链表的合并,每次两两合并相邻的两个有序序列,直至整个序列有序。
主要思想:基数排序是按照低位先排序,然后收集;再按照高位排序,然后再收集;依次类推,直到最高位。
完整代码
#define Radix 10
#define MaxDigit 4
typedef struct ENode{ //定义元素结点
int data;
struct ENode *next;
}*PtrToNode;
typedef struct BucketNode{ //定义桶结点结构
PtrToNode head;
PtrToNode tail;
}*Bucket;
void LSDRadix_Sort(int A[], int N){ //基排序
int i, D; //D为位, d为第D位上的数字(范围为0到9)
//定义两个大小为Radix的桶,并初始化
Bucket B1 = malloc(Radix * sizeof(struct BucketNode));
Bucket B2 = malloc(Radix * sizeof(struct BucketNode));
for(i=0; i<Radix; i++){
B1[i].head = B1[i].tail = B2[i].head = B2[i].tail = NULL; //注意大bug:B1为桶指针,但是B1[i]为结构体
}
//将数组中元素按照倒数第D位数字分别挂到桶B1上
D = 1;
Transfer_Array_To_Bucket(A, B1, N, D);
D++;
//开始相互倒腾,每倒腾一趟就往前看一位
while(D <= MaxDigit){
if(D % 2 == 0)
Transfer_Bucket_To_Bucket(B1, B2, D);
else
Transfer_Bucket_To_Bucket(B2, B1, D);
D++;
}
//倒腾结束后将桶中的元素依次倒入数组A中
if(D % 2 == 0)
Transfer_Bucket_To_Array(B1, A, N);
else
Transfer_Bucket_To_Array(B2, A, N);
//释放两个桶及其元素
Free_Bucket(B1);
Free_Bucket(B2);
return;
}
void Transfer_Array_To_Bucket(int A[], Bucket B, int N, int D){ //将数组A中元素按照第D位挂到桶B中
int i, d;
PtrToNode temp;
for(i=0; i<N; i++){
d = Get_Digit(A[i], D); //获取A[i]倒数第D位数字
temp = malloc(sizeof(struct ENode)); //创建一个新结点并初始化
temp->data = A[i];
temp->next = NULL;
if(B[d].tail == NULL){ //若桶的d位置上为空
B[d].head = B[d].tail = temp;
}else{
B[d].tail->next = temp;
B[d].tail = temp;
}
}
return;
}
void Transfer_Bucket_To_Array(Bucket B, int A[], int N){ //将桶B1中元素依次倒入数组A中,最多不超过N
int k, i = 0;
PtrToNode p;
for(k=0; k<Radix; k++){
p = B[k].head;
while(p != NULL){
if(i < N){
A[i++] = p->data;
p = p->next;
}else{
return;
}
}
}
return;
}
void Transfer_Bucket_To_Bucket(Bucket B1, Bucket B2, int D){ //依次将桶B1中元素按照第D位挂到B2中,
int k, d;
PtrToNode p, temp;
//依次从B1中取下元素结点,根据D位数字挂到B2上
for(k=0; k<Radix; k++){
p = B1[k].head;
while(p != NULL){
//从B1中取该元素,并获取第D位数字
temp = p;
p = p->next;
d = Get_Digit(temp->data, D); //获取该结点第D位数字
//将该元素挂到B2上
temp->next = NULL; //肯定作为本次转移的尾结点
if(B2[d].head == NULL){ //若B2[d]为空位置
B2[d].head = B2[d].tail = temp;
}else{ //若B2[d]不为空位置,则将temp结点接到尾结点上
B2[d].tail->next = temp;
B2[d].tail = temp;
}
}
//取完B1[k]上的所有结点后,设置其首尾结点指针为空
B1[k].head = B1[k].tail = NULL;
}
return;
}
int Get_Digit(int X, int D){ //获取X倒数第D位数字
int k, i;
for(i=0; i<D-1; i++)
X = X / Radix;
k = X % Radix;
return k;
}
复杂度与稳定性的比较
| 算法类别 | 平均时间复杂度 | 最好情况复杂度 | 最坏情况复杂度 | 空间复杂度 | 稳定性 |
|---|---|---|---|---|---|
| 冒泡排序 | \(O(n^2)\) | \(O(n)\) | \(O(n^2)\) | \(O(1)\) | 稳定 |
| 选择排序 | \(O(n^2)\) | \(O(n^2)\) | \(O(n^2)\) | \(O(1)\) | 不稳定 |
| 插入排序 | \(O(n^2)\) | \(O(n)\) | \(O(n^2)\) | \(O(1)\) | 稳定 |
| 希尔排序 | \(O(n^{1.5})\) | - | - | \(O(1)\) | 不稳定 |
| 堆排序 | \(O(n log(n))\) | \(O(n log(n))\) | \(O(n log(n))\) | \(O(1)\) | 不稳定 |
| 快速排序 | \(O(n log(n))\) | \(O(n log(n))\) | \(O(n^2)\) | \(O(1)\) | 不稳定 |
| 归并排序 | \(O(n log(n))\) | \(O(n log(n))\) | \(O(n log(n))\) | \(O(n)\) | 稳定 |
| 基排序 | \(O(d*n)\) | \(O(d*n)\) | \(O(d*n)\) | \(O(n)\) | 稳定 |
以下是基于浙大数据结构课练习题测试(09-排序1 排序 (25 分))。
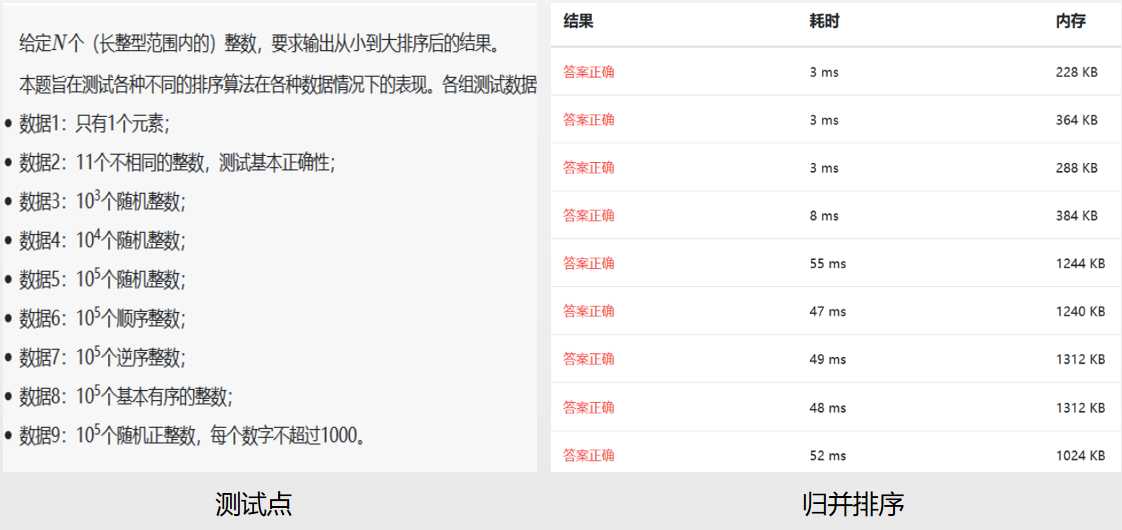
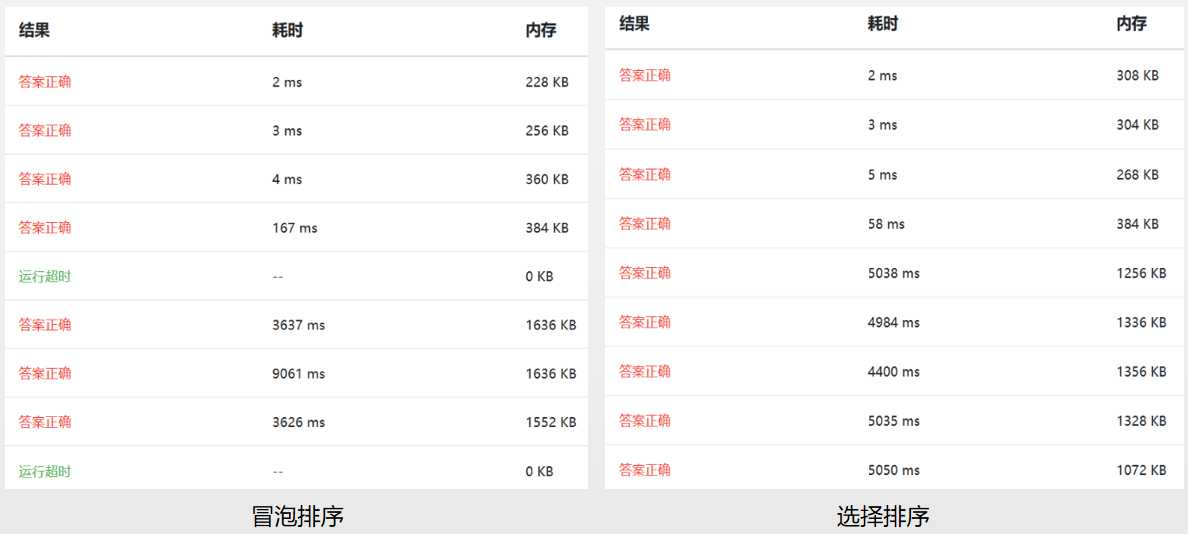
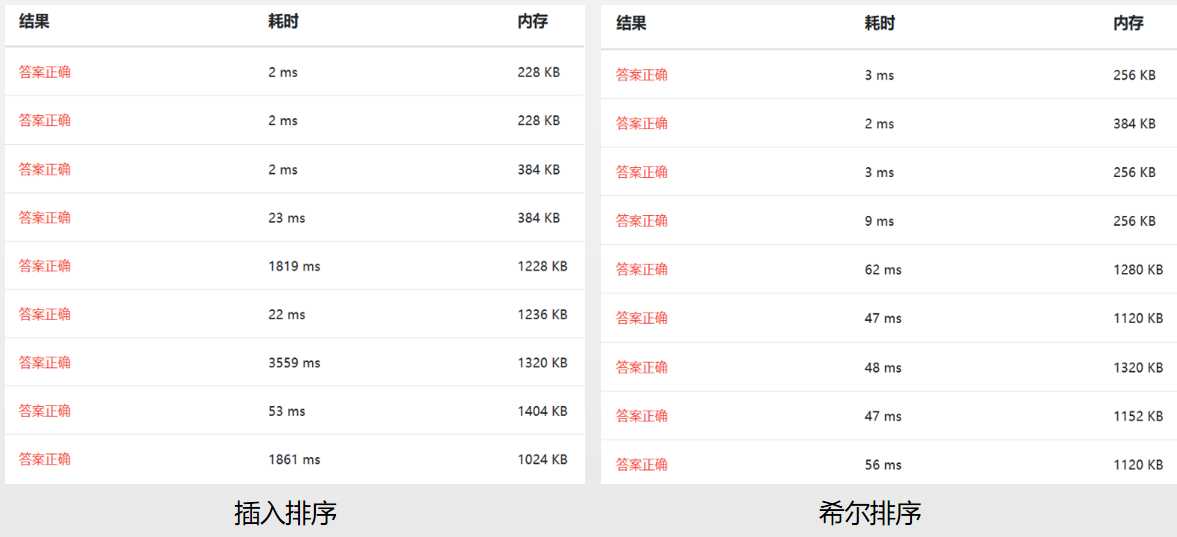
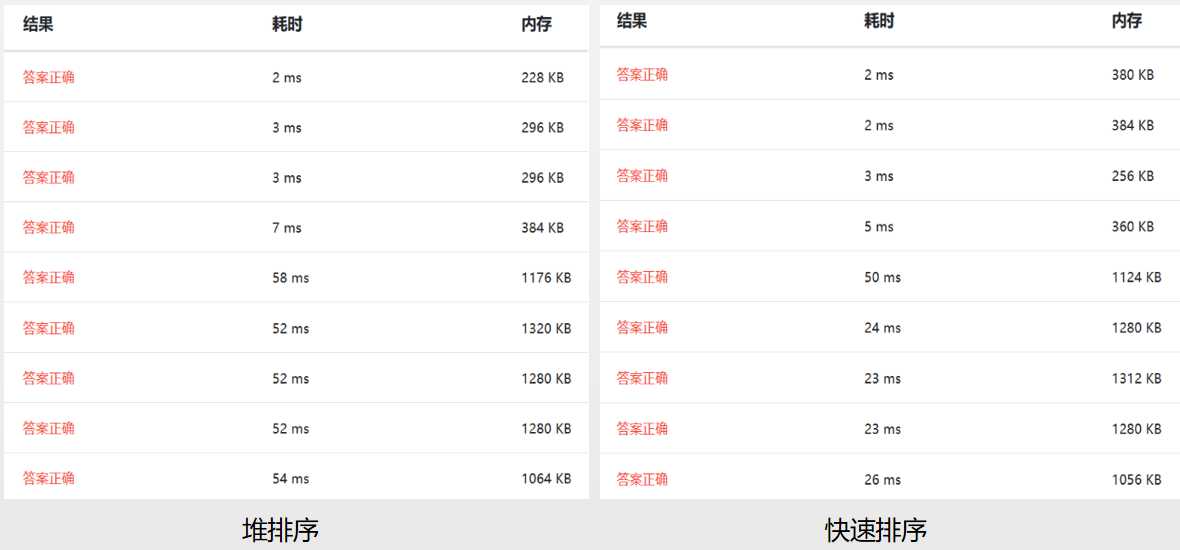
参考:
https://blog.csdn.net/qq_39207948/article/details/80006224
https://www.cnblogs.com/onepixel/articles/7674659.html
https://www.runoob.com/w3cnote/sort-algorithm-summary.html
标签:The 合并 merge blog 副本 二叉树 github radix for
原文地址:https://www.cnblogs.com/inchbyinch/p/11630388.html