标签：bool   二维   图片   static   list   tar   div   targe   查找   

问题描述

题目描述
在一个二维数组中(每个一维数组的长度相同),每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序.请完成一个函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
要求
时间限制:1秒
空间限制:32768K

方法原型

public boolean find(int target, int [][] array)

输入输出例子
在以下二维数组中

{
        {1,2,8,9},
        {2,4,9,12},
        {4,7,10,13},
        {6,8,11,15}
}

查找4, 应该返回true.

解题思路

审题后可知这个题有两个可以简化解题的关键点，一个是只需要判断数组中有否某数字存在，而不需要知道具体数目或位置。
其次是数组中的行、列都是有序的，这可以加快我们查找的速度。
为什么说行、列都是有序的可以加快我们查找的速度呢？我么先把问题简化成一维数组讨论，假设有一个升序的一维数组，那么从头开始遍历数组，如果当前遍历的数字大于要查找的数字，则因为该数组升序，所以之后的所有数字都大于要查找的数字，利用这个性质，我们可以跳过很多不必要的遍历，加快查找的速度。
将一维数组扩展为题目所述的二维数组，结论就是：从数组的左上角开始遍历，如果当前遍历的数字大于要查找的数字，则当前行及往下的所有行的往右所有列的数字都大于要查找的数字（不合格，不需要遍历）。
以上的话说起来比较拗口，我们通过下图加以说明：

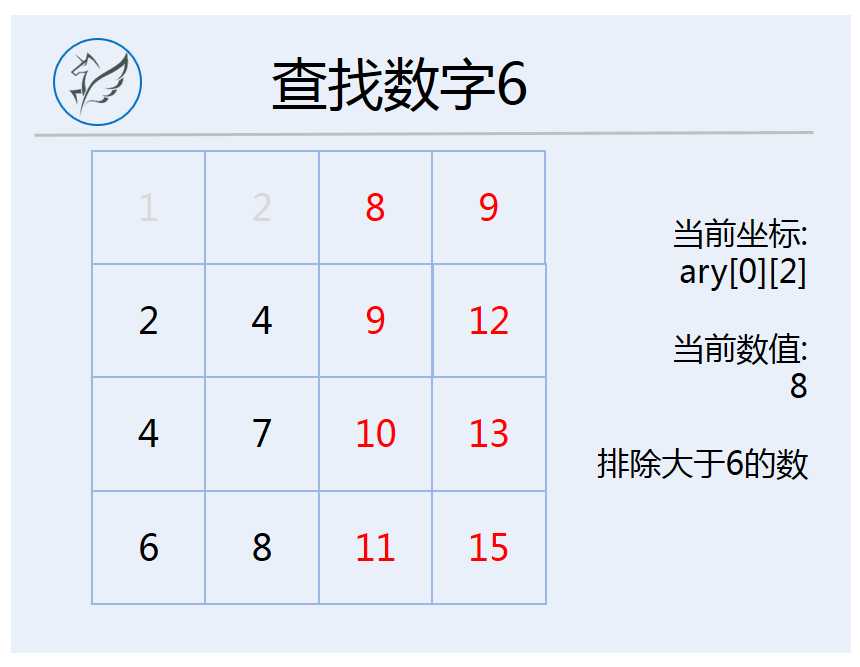
如果在图示数组中，寻找是否存在数字6，当前正遍历到0行2列，并且发现其中的元素8是大于6的，那么图示的所有标红的位置的数字，必然全部都大于6，可以在后续的遍历中直接排除。

以下动图展示在一个二维数组中，完整查找数字6的过程：

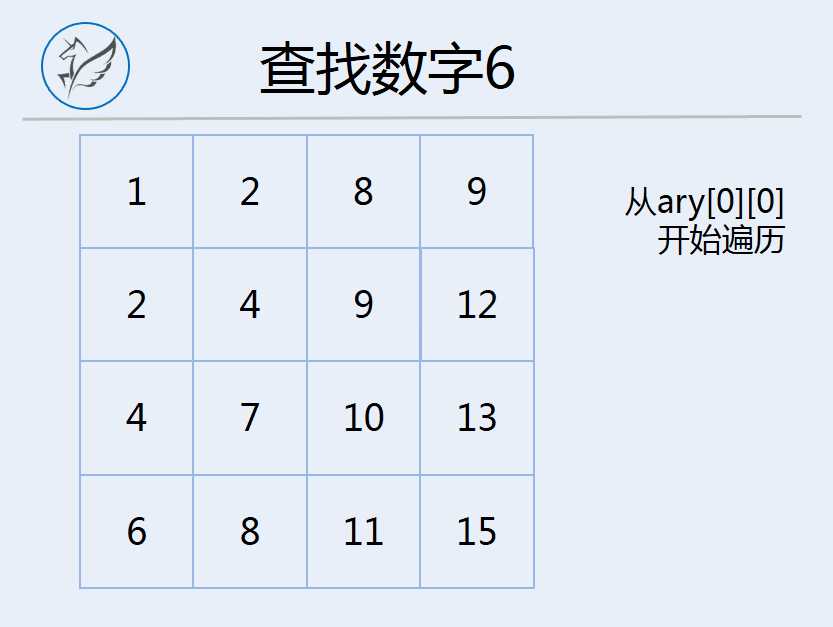
其实，以上的过程理解后，这种批量排除的算法可以进一步优化，那就是每次从剩余有效的二维数组的右上角作为起点开始遍历，这样效率更高的原因是，不仅可以批量排除大于目标数的数字，还可以批量淘汰小于目标数的数字：

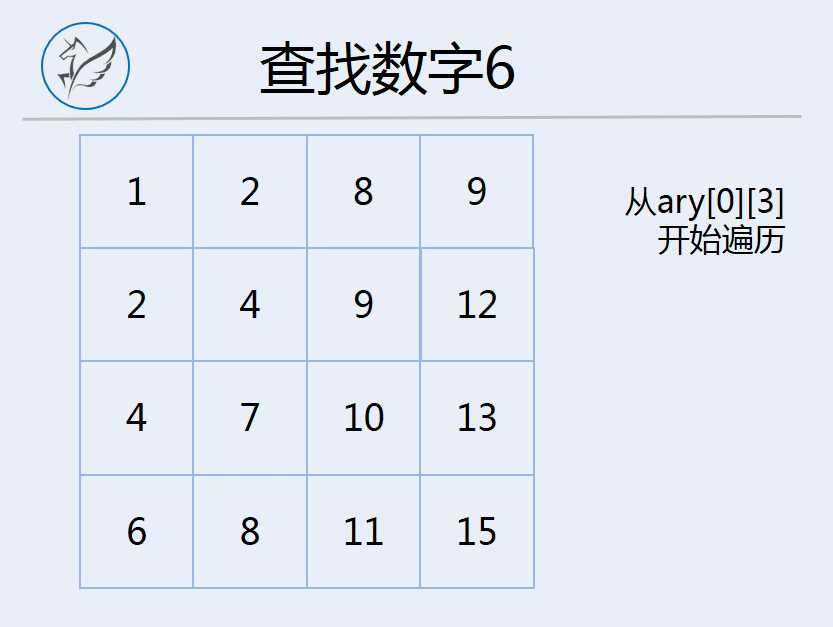
因为后一种方法的遍历逻辑更简单，效率也更高，因此我们最终采用这种解法。

相关代码

package com.shellmad;

public class Solution {
    public static void main(String[] args) {
        Solution solution = new Solution();
        int[][] array = {
                {1,2,8,9},
                {2,4,9,12},
                {4,7,10,13},
                {6,8,11,15}
        };

        if (solution.find(6, array)) {
            System.out.println("找到");
        } else {
            System.out.println("没找到");
        }
    }

    public boolean find(int target, int [][] array) {

        // 检查输入
        if (array == null || array.length == 0 || array[0].length == 0) {
            return false;
        }

        int rows = array.length;
        int row = 0;
        int column = array[0].length - 1;

        // 遍历二维数组
        while (row < rows && column >= 0) {

            if (array[row][column] == target) {
                return true;
            } else if (array[row][column] > target) {
                column--;
            } else {
                row++;
            }
        }
        return false;
    }
}

经典算法题-基础-二维数组中的查找

标签：bool   二维   图片   static   list   tar   div   targe   查找   

原文地址：https://www.cnblogs.com/shellmad/p/11638562.html