标签:应该 ret cst algorithm 技术 ora color 堆优化 const
小P和小R在玩一款益智游戏。游戏在一个正权有向图上进行。 小P 控制的角色要从A 点走最短路到B 点,小R 控制的角色要从C 点走最短路到D 点。 一个玩家每回合可以有两种选择,移动到一个相邻节点或者休息一回合。 假如在某一时刻,小P 和小R 在相同的节点上,那么可以得到一次特殊奖励,但是在每 个节点上最多只能得到一次。 求最多能获得多少次特殊奖励
第一行两个整数n,m 表示有向图的点数和边数。 接下来m 行每行三个整数xi,yi,li,表示从xi 到yi 有一条长度为li 的边。 最后一行四个整数A,B,C,D,描述小P 的起终点,小R 的起终点。
输出一个整数表示最多能获得多少次特殊奖励。若小P不能到达B点或者小R不能到达D点则输出-1。
5 5
1 2 1
2 3 2
3 4 4
5 2 3
5 3 5
1 3 5 4
2
提示
对于30%的数据,满足n≤50 对于60%的数据,满足n≤1000,m≤5000 对于100%的数据,满足n≤50000,m≤200000,1≤li≤500000000
分析
A到B,C到D的最短路有很多条。
但对于任意一条A到B的最短路和任意一条C到D的最短路如果他们有交点,那交点一定是连续的,否则一定存在交点更多的两条最短路。
如图
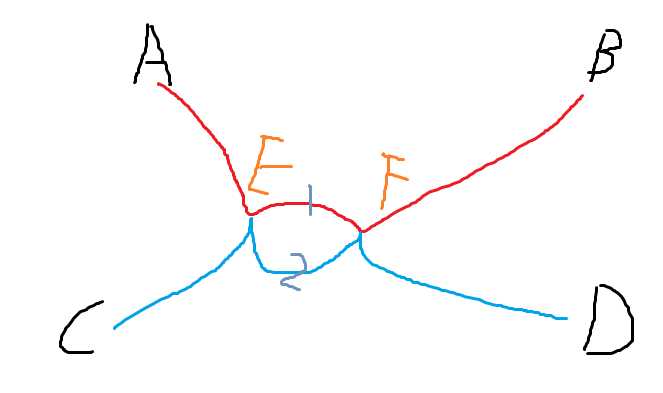
如果A到B的路径(红色)与C到D的路径(蓝色)有不连续的交点E与F
那么E通过路径1到达F与E通过路径2到达F的距离应该是一样,否则路径A-B,路径C-D中有一条不是最短路
此时,若A走到达E后走路径2到达F会与路径C-D有更多交点
即走绿色这条路<-也是最短路
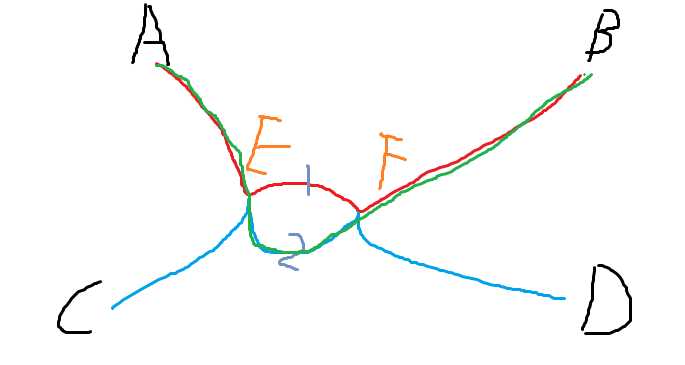
所以最优方案中特殊奖励的点一定是连续的。
于是我们可以用同时在A-B最短路上和C-D最短路上的有向边构成一个新图
那么新图一定是一个有向无环图,但不一定联通
最后对新图拓扑排序dp最长链即可
代码(给你们演示一下堆优化的SPFA)
#include<queue>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn=50005;
const int maxm=200005;
struct node{int id;long long d;};
bool operator <(node a,node b){return a.d>b.d;}
int info[maxn],nx[maxm<<1],v[maxm<<1],w[maxm<<1],re[maxm<<1];long long d[5][maxn];
int n,m,en,ans,ecnt,p[5],dp[maxn],vis[maxn],inp[maxn],top[maxn],lef[maxm<<1];priority_queue<node>q;
void add(int u1,int v1,int w1,int r){nx[++ecnt]=info[u1];info[u1]=ecnt;v[ecnt]=v1;w[ecnt]=w1;re[ecnt]=r;}
void SPFA(int k)
{
memset(vis,0,sizeof vis);
d[k][p[k]]=0;q.push((node){p[k],0});
while(!q.empty())
{
node nw=q.top();q.pop();
if(vis[nw.id]==1)continue;vis[nw.id]=1;d[k][nw.id]=nw.d;
for(int i=info[nw.id];i;i=nx[i])
if(!((k%2)^re[i])&&d[k][v[i]]>nw.d+w[i])q.push((node){v[i],nw.d+w[i]});
}
}
int main()
{
scanf("%d%d",&n,&m);memset(d,0x7f,sizeof d);
for(int i=1,u1,v1,w1;i<=m;i++)scanf("%d%d%d",&u1,&v1,&w1),add(u1,v1,w1,1),add(v1,u1,w1,0);
for(int k=1;k<=4;k++)scanf("%d",&p[k]),SPFA(k);
if(d[1][p[2]]==d[0][0]||d[3][p[4]]==d[0][0]){puts("-1");return 0;}
for(int x=1;x<=n;x++)
{
for(int e=info[x];e;e=nx[e])
if(re[e]&&d[1][x]+w[e]+d[2][v[e]]==d[1][p[2]]&&d[3][x]+w[e]+d[4][v[e]]==d[3][p[4]])
lef[e]=1,inp[v[e]]++;
}
for(int x=1;x<=n;x++)if(inp[x]==0)top[++en]=x,dp[x]=1;
for(int i=1;i<=en;i++)
{
int nw=top[i];
for(int e=info[nw];e;e=nx[e])
if(lef[e])
{
dp[v[e]]=max(dp[v[e]],dp[nw]+1);
ans=max(ans,dp[v[e]]);inp[v[e]]--;
if(!inp[v[e]])top[++en]=v[e];
}
}
printf("%d\n",ans);
}
标签:应该 ret cst algorithm 技术 ora color 堆优化 const
原文地址:https://www.cnblogs.com/firecrazy/p/11656407.html