标签：car   algo   dong   spl   col   mamicode   复杂   roc   出现   

字符串匹配算法

原文摘录：https://www.cnblogs.com/gaochundong/p/string_matching.html

首先是一系列概念定义：

• 文本Text: 是一个长度为n的数组T[1..n]  (??这里第一位置索引是数字1)
• 模式Pattern: 是一个长度为m的数组P[1..m],  并且m<=n.
• T和P的元素都属于有限的字母表Σ 表
• 概念：有效位移Valid Shift（用字母s代表）。即P在T中出现，并且位置移动s次。如果0<=  s <= n-m ,并且T[s+1..s+m] = P[1..m]，则s是有效位移。

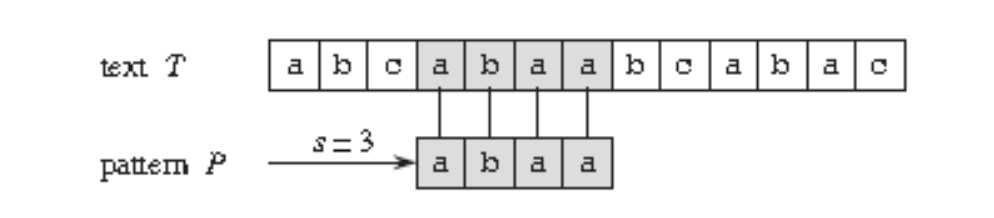
 上图的有效位移是3。

解决字符串的算法非常多：

朴素算法（Naive Algorithm）、Rabin-Karp 算法、有限自动机算法（Finite Automation）、 Knuth-Morris-Pratt 算法（即 KMP Algorithm）、Boyer-Moore 算法、Simon 算法、Colussi 算法、Galil-Giancarlo 算法、Apostolico-Crochemore 算法、Horspool 算法和 Sunday 算法等。

字符串匹配算法通常分为2个步骤：预处理和匹配。算法的总运行时间是两者之和。

下文举例：

• 朴素的字符串匹配算法（Naive String Matching Algorithm）
• Knuth-Morris-Pratt 字符串匹配算法（即 KMP 算法）
• Boyer-Moore 字符串匹配算法

   

   

朴素的字符串匹配算法（Naive String Matching Algorithm）

就是穷举法，枚举法，也叫暴力匹配。是最低效最原始的算法。特点：

1. 无预处理阶段。（因为是暴力匹配）
2. 对Pattern，可以从T的首或尾开始逐个匹配字母，比较顺序没有限制。
3. 最坏时间复杂度O((n-m+1)*m).

方法是使用循环来检查是否在范围n-m+1中存在满足条件P[1..m] = T[s+1..s+m]的有效位移s。

伪代码：

Native_string_matcher(T, P)
  n <- length[T]
  m <- length[P]
  for s <- 0 to n - m
    do if P[1..m] = T[s+1..s+m]
       then print "Pattern occurs with shift"

Knuth-Morris-Pratt 字符串匹配算法（即 KMP 算法）

这是对Pattern进行预处理的算法。

我的理解是：

P中是否有重复的字符串。对自身匹配，逐个位移，并记录位移后，能够匹配（重复）几个字符。然后在实际和其他文本进行匹配时，就可以利用已知的信息，减少重复比较。

字符串匹配算法

标签：car   algo   dong   spl   col   mamicode   复杂   roc   出现   

原文地址：https://www.cnblogs.com/chentianwei/p/11665656.html