标签:return invalid result tar kth 块代码 des 否则 结构
结对成员:钟苑莉 张冰微
一、 Github项目地址:https://github.com/Clarazhangbw/ruangongjd
二、PSP表格
|
PSP2.1 |
Personal Software Process Stages |
预估耗时(分钟) |
实际耗时(分钟) |
|
Planning |
计划 |
30 |
30 |
|
· Estimate |
· 估计这个任务需要多少时间 |
30 |
30 |
|
Development |
开发 |
1960 |
2270 |
|
· Analysis |
· 需求分析 (包括学习新技术) |
120 |
150 |
|
· Design Spec |
· 生成设计文档 |
40 |
50 |
|
· Design Review |
· 设计复审 (和同事审核设计文档) |
20 |
30 |
|
· Coding Standard |
· 代码规范 (为目前的开发制定合适的规范) |
30 |
30 |
|
· Design |
· 具体设计 |
60 |
80 |
|
· Coding |
· 具体编码 |
1600 |
1800 |
|
· Code Review |
· 代码复审 |
30 |
40 |
|
· Test |
· 测试(自我测试,修改代码,提交修改) |
60 |
90 |
|
Reporting |
报告 |
80 |
110 |
|
· Test Report |
· 测试报告 |
30 |
50 |
|
· Size Measurement |
· 计算工作量 |
20 |
20 |
|
· Postmortem & Process Improvement Plan |
· 事后总结, 并提出过程改进计划 |
30 |
40 |
|
合计 |
|
2070 |
2410 |
三、效能分析
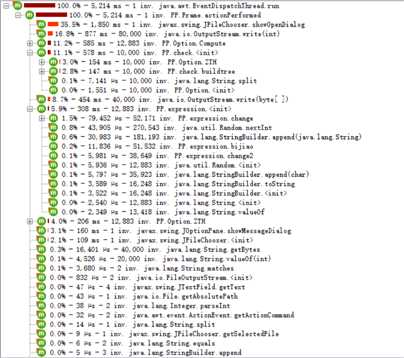

通过Jprofiler进行效能分析,产生10000道题共耗时5,214ms,其中消耗最大的函数是JFileChooser.showOpenDialog(),耗时1,850ms,占35.5%。经分析后,原因可能在于用户在界面上选择文件时需要时间选择,因此需要等待用户选择的时间。
本次效能分析我们在利用工具得到代码运行时间前已经逐一优化了,比如产生表达式时利用表达式的格式分配随机数去判断括号个数及位置,以及在查重时改变原有的判断二叉树每一个结点然后调换左右子树进行查重分析的方式,利用+或*的数量及用结点列表记录+或*的位置进行重构相应的二叉树再进行重复判断。这些过程的改进都是优化代码效率的过程,因此最后运用JProfiler进行效能分析时,也得到了较为满意的结果。证明了在代码思路设计过程中我们的优化都是有效的。
四、设计实现过程
1.模块化实现过程
首先从用户需求出发,通过界面获取用户输入的题目数值范围和题目数量。先针对产生一道有效表达式进行分析,产生一道有效表达式大体分为三个步骤:第一个步骤是随机生成一道表达式,我们用expression模块实现。第二个步骤是对随机生成的表达式进行计算,得到计算结果,并在计算过程中将不符合题目规则的表达式标记为无效。此步骤我们用option模块实现。第三个步骤是查重,查重步骤主要思路是将计算后产生的初步有效表达式与有效表达式进行逐一比较,若重叠则舍弃当前产生的初步有效表达式,若不重叠则将表达式放入有效表达式数组中,便于后续写入用户选择的题目文件中。此步骤用check模块实现。上述为产生一道有效表达式的主要过程,根据用户输入的题目数量,循环以上步骤,产生规定数量的有效表达式。最后将有效表达式题目写进题目文件,同时将有效表达式的答案写入当前目录下的答案文件。通过比较标准文件和用户答案文件生成校对文件。
2.各模块的具体实现过程
设计用户界面,通过用户输入,获取用户规定的题目数量以及题目数值范围,当用户点击“生成”按钮时,获取用户选择的题目文件路径,程序调用expression模块,option模块、check模块,不断循环产生经过计算查重后规定数量的有效表达式并写入题目文件中,同时将计算过程中产生的有效表达式的标准答案写入答案文件中。当用户点击“校对”按钮时,获取用户选择的标准答案文件,再获取用户选择的需要校对的用户答案文件。将校对后的结果按照规定的格式写入校对文件中。图形界面作为程序与用户的交互媒介,能够通过得到用户每一次输入的题目数量及数值范围,可多次生成符合用户需求的文件。
expression模块作用是产生随机表达式。设计思路是,在构造方法中,利用标记分别控制表达式符号的个数及种类,数值的类型,表达式中括号对的数量及位置,随机产生一条表达式。另外,有三个辅助函数,change()函数将随机生成的数值转换为自然数或真分数的形式,change2()函数将控制符号种类的随机数转为对应的符号字符,bijiao()函数判断生成的数值是否在用户规定的数值范围内。
option模块的作用是计算随机生成的表达式的结果,并将不符合题目要求的表达式(计算过程中出现负数或除数为0)标记为无效。具体思路体现为,首先通过ZTH()函数将随机生成的表达式转化为后缀表达式,利用栈的性质,用栈来存储运算符,越往栈顶优先级越高,越先计算,最终得到表达式的运算结果。在该过程中调用operate()函数,通过将数值统一转化为分数的形式,计算单个运算符与两个数值的运算结果。并设计faddf()函数,fminusf()函数,fmulf()函数,fdevf()函数实现两个分数具体的加减乘除运算过程。
check模块的功能是将计算后的初步有效表达式与有效表达式进行比较,最终确定新的有效表达式。主要思路为,首先比较当前表达式与有效表达式的符号个数,若符号个数相同,进行进一步查重。调用option模块的KTH()函数将两个表达式转为后缀表达式,再调用buildtree()函数将后缀表达式转换为二叉树,返回广度搜索后的结点列表。check2()函数中,依据+或*数量及在表达式中的位置,产生与其同构的所有二叉树,再调用postOrderRe()将各种情况下要比较的两棵二叉树转换为后缀表达式进行匹配。如果相同,说明该表达式与有效表达式重叠,如果不相同,则将当前表达式放进有效表达式数组中。
3.各模块及模块内函数关系图
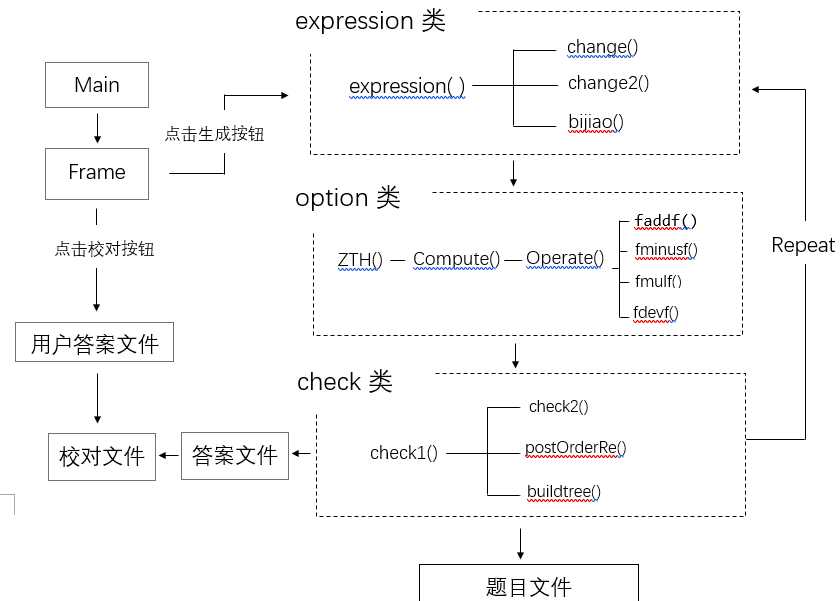
五、代码说明
1.随机产生表达式
Random random=new Random(); int tag=1; String expression1=new String(); //放表达式 int fhnum=0; //放表达式的符号个数 int i=1; int row1=(int) (random.nextInt(4)); //第一个运算符的种类 0:+ 、1:-、2:×、3:÷ int row2=(int) (random.nextInt(4)); //第二个运算符的种类 0:+ 、1:-、2:×、3:÷ int row3=(int) (random.nextInt(4)); //第三个运算符的种类 0:+ 、1:-、2:×、3:÷ int kuh1=(int) (random.nextInt(2)); //括号 0:有括号,1:无括号 int kuh2=(int) (random.nextInt(2)); //两个运算符时,有括号的话是加在哪个位置 int kuh3=(int) (random.nextInt(3)); //三个运算符时,有一个括号的话是加在哪个位置‘ int kuh4=(int) (random.nextInt(5)); //三个运算符时,有二个括号的话是加在哪个些位置 public expression(int b) { char fuhao1=change2(row1); //随机数控制符号种类 char fuhao2=change2(row2); char fuhao3=change2(row3); int range=b; //题目中的数值范围 int number=(int) (random.nextInt(3)+1); //随机数,控制运算符个数 int tag1=(int) (random.nextInt(2)); //利用分母是否等于1控制生成的随机数是整数还是分数 int tag2=(int) (random.nextInt(2)); int tag3=(int) (random.nextInt(2)); int tag4=(int) (random.nextInt(2)); int z1,m1,z2,m2,z3,m3,z4,m4; boolean t; do { z1=(int) (random.nextInt(range)); //分子1 m1=(int) (random.nextInt(range)+1); //分母1 if(tag1==1) m1=1; t=bijiao(z1,m1,range); }while(!t); do { z2=(int) (random.nextInt(range)); //分子2 m2=(int) (random.nextInt(range)+1); //分母2 if(tag2==1) m2=1; t=bijiao(z2,m2,range); }while(!t); do{ z3=(int) (random.nextInt(range)); //分子3 m3=(int) (random.nextInt(range)+1); //分母3 if(tag3==1) m3=1; t=bijiao(z3,m3,range); }while(!t); do { z4=(int) (random.nextInt(range)); //分子4 m4=(int) (random.nextInt(range)+1); //分母4 if(tag4==1) m4=1; t=bijiao(z4,m4,range); }while(!t); fhnum=number; if(number==1) {//只有一个运算符的情况 expression1=change(z1,m1)+" "+fuhao1+" "+change(z2,m2)+" "+"="; } if(number==2) {//有两个运算符的情况 if(kuh1==0) {//表达式中无括号 expression1=change(z1,m1)+" "+fuhao1+" "+change(z2,m2)+" "+fuhao2+" "+change(z3,m3)+" "+"="; } else {//表达式中有括号 if(kuh2==0) {//随机数kuh2为0时括号在前面 expression1="("+" "+change(z1,m1)+" "+fuhao1+" "+change(z2,m2)+" "+")"+" "+fuhao2+" "+change(z3,m3)+" "+"="; } else if(kuh2==1) {//随机数kuh2为1时括号在后面 expression1=change(z1,m1)+" "+fuhao1+" "+"("+" "+change(z2,m2)+" "+fuhao2+" "+change(z3,m3)+" "+")"+" "+"="; } } } if(number==3) {//有三个运算符的情况 if(kuh1==0) {//表达式中无括号 expression1=change(z1,m1)+" "+fuhao1+" "+change(z2,m2)+" "+fuhao2+" "+change(z3,m3)+" "+fuhao3+" "+change(z4,m4)+" "+"="; } else if(kuh1==1) {//表达式中有括号 if(kuh2==0) {//表达式有一对括号 switch(kuh3) {//利用kuh3的值控制括号的位置 case 0: expression1="("+" "+change(z1,m1)+" "+fuhao1+" "+change(z2,m2)+" "+")"+" "+fuhao2+" "+change(z3,m3)+" "+fuhao3+" "+change(z4,m4)+" "+"="; case 1: expression1=change(z1,m1)+" "+fuhao1+" "+"("+" "+change(z2,m2)+" "+fuhao2+" "+change(z3,m3)+" "+")"+" "+fuhao3+" "+change(z4,m4)+" "+"="; case 2: expression1=change(z1,m1)+" "+fuhao1+" "+change(z2,m2)+" "+fuhao2+" "+"("+" "+change(z3,m3)+" "+fuhao3+" "+change(z4,m4)+" "+")"+" "+"="; } }else if(kuh2==1) {//表达式有两对括号 switch(kuh4) {//利用kuh4的值控制括号的位置 case 0: expression1="("+" "+"("+" "+change(z1,m1)+" "+fuhao1+" "+change(z2,m2)+" "+")"+" "+fuhao2+" "+change(z3,m3)+" "+")"+" "+fuhao3+" "+change(z4,m4)+" "+"="; case 1: expression1="("+" "+change(z1,m1)+" "+fuhao1+" "+change(z2,m2)+" "+")"+" "+fuhao2+" "+"("+" "+change(z3,m3)+" "+fuhao3+" "+change(z4,m4)+" "+")"+" "+"="; case 2: expression1="("+" "+change(z1,m1)+" "+fuhao1+" "+"("+" "+change(z2,m2)+" "+fuhao2+" "+change(z3,m3)+" "+")"+" "+")"+" "+fuhao3+" "+change(z4,m4)+" "+"="; case 3: expression1=change(z1,m1)+" "+fuhao1+" "+"("+" "+"("+" "+change(z2,m2)+" "+fuhao2+" "+change(z3,m3)+" "+")"+" "+fuhao3+" "+change(z4,m4)+" "+")"+" "+"="; case 4: expression1=change(z1,m1)+" "+fuhao1+" "+"("+" "+change(z2,m2)+" "+fuhao2+" "+"("+" "+change(z3,m3)+" "+fuhao3+" "+change(z4,m4)+" "+")"+" "+")"+" "+"="; } } } } }
2.计算单个表达式的结果
public class option { int tagg=1; //减运算过程中是否出现负数或除运算过程中分母是否为0的标记 String result=" "; //用于存放表达式的运算结果 String f1=" "; //用于存放通分后的第一个分数 String f2=" "; //用于存放通分后的第二个分数 public String ZTH(String s){ //用于将中缀表达式转换为后缀表达式的函数 String h=" "; Stack<String> os=new Stack<String>(); //利用栈存储运算符,越往栈顶的优先级越高 String[] ex=s.split(" "); int l=ex.length; for(int i=0;i<l-1;i++) //l-1,因为表达式最后一个是=,不用加进去 { String part=ex[i]; switch(part){ case "+": case "-": while(os.size()!=0){ String s1=os.pop(); if(s1.equals("(")){ os.push(s1); //将(重新压进栈,然后退出循环 break; } h=h+s1+" "; } os.push(part); break; case "*": case "÷": while(os.size()!=0){ String s2=os.pop(); if(s2.equals("+")||s2.equals("-")||s2.equals("(")){ os.push(s2); break; }else{ h=h+s2+" "; } } os.push(part); break; case "(": os.push(part); break; case ")": //遇到)就把栈中的运算符弹出直到遇到( while(os.size()!=0){ String s3=os.pop(); if(s3.equals("(")){ break; }else{ h=h+s3+" "; } } break; default: //part为数值的情况 h=h+part+" "; break; } } while(os.size()!=0){ //将最后栈中剩余的运算符一并弹出 h=h+os.pop()+" "; } return h; } public void Compute(String s){ //利用后缀表达式计算表达式的结果 tagg=1; //初始化tagg Stack<String> cs=new Stack<String>(); //用于计算的栈 result=" "; //初始化,用于保存计算结果 String[] hex=s.split(" "); //这里我们从第hex[1]开始,因为0那个是空格 int l1=hex.length; for(int j=1;j<l1;j++){ //从左到右遍历后缀表达式 if(hex[j].matches("\\d+")||hex[j].matches("\\d+/\\d+")||hex[j].matches("\\d+‘\\d+/\\d+")){ cs.push(hex[j]); //如果遍历到的是数值则直接入栈 } else{ //如果遍历到的是运算符,将栈顶的两个数值弹出,计算结果后,再将结果压进栈 String s1=cs.pop(); String s2=cs.pop(); result=Operate(hex[j],s2,s1); cs.push(result); if(tagg==0)break; //如果标记为0,停止计算,此时的result是无效的 } } result=cs.pop(); } public String Operate(String op,String s1,String s2){ //计算最简表达式 String result=" "; //将两个数值统一化为分数的形式进行计算 if(s1.matches("\\d+")){ //将自然数s1化为分数,分母为1 f1=s1+"/"+1; } if(s1.matches("\\d+/\\d+")){ f1=s1; } if(s1.matches("\\d+‘\\d+/\\d+")){ //如果s1为" ‘ / "这种形式,将其化为假分数 String[] ss1=s1.split("‘"); String sz1=ss1[0]; String sf=ss1[1]; String[] sff=sf.split("/"); String sfz=sff[0]; String sfm=sff[1]; int z1=Integer.parseInt(sz1); int fz=Integer.parseInt(sfz); int rfm=Integer.parseInt(sfm); int rfz=z1*rfm+fz; f1=rfz+"/"+rfm; } if(s2.matches("\\d+")){ //s2的转化规则与s1相同 f2=s2+"/"+1; } if(s2.matches("\\d+/\\d+")){ f2=s2; } if(s2.matches("\\d+‘\\d+/\\d+")){ String[] ss2=s2.split("‘"); String sz2=ss2[0]; String sf=ss2[1]; String[] sff=sf.split("/"); String sfz=sff[0]; String sfm=sff[1]; int z2=Integer.parseInt(sz2); int fz=Integer.parseInt(sfz); int rfm=Integer.parseInt(sfm); int rfz=z2*rfm+fz; f2=rfz+"/"+rfm; } switch(op){ //判断操作符属于哪一类 case "+": result=faddf(f1,f2); break; case "-": result=fminusf(f1,f2); break; case "*": result=fmulf(f1,f2); break; case "÷": result=fdevf(f1,f2); break; } return result; } public String faddf(String s1,String s2){ //实现两个分数相加 String[] s11=s1.split("/"); //分别获得两个分数的分子分母 String sfz1=s11[0]; String sfm1=s11[1]; String[] s22=s2.split("/"); String sfz2=s22[0]; String sfm2=s22[1]; int fz1=Integer.parseInt(sfz1); int fm1=Integer.parseInt(sfm1); int fz2=Integer.parseInt(sfz2); int fm2=Integer.parseInt(sfm2); int y1=fz1*fm2; //对两个分数进行通分 int y2=fz2*fm1; int y3=y1+y2; int rfm=fm1*fm2; if(rfm==1)return String.valueOf(y3); //如果和的分母为1,直接输出分子 int z=y3/rfm; int rfz=y3-z*rfm; if(rfz==0)return String.valueOf(z); //分数化简后只剩下整数部分 else if(z==0)return rfz+"/"+rfm; //和的整数部分为0且分数部分不为0的情况 else return z+"‘"+rfz+"/"+rfm; //和的整数部分和分数部分都不为0的情况 } public String fminusf(String s1,String s2){ //实现两个分数相减 String[] ss1=s1.split("/"); //分别获得两个分数的分子分母 String sfz1=ss1[0]; String sfm1=ss1[1]; int fz1=Integer.parseInt(sfz1); int fm1=Integer.parseInt(sfm1); String[] ss2=s2.split("/"); String sfz2=ss2[0]; String sfm2=ss2[1]; int fz2=Integer.parseInt(sfz2); int fm2=Integer.parseInt(sfm2); int z1m2=fz1*fm2; //对这两个分数进行通分 int z2m1=fz2*fm1; int rfm=fm1*fm2; int cha=z1m2-z2m1; if(rfm==1){ //如果得到的两个分数的差的分母为1 if(cha<0){tagg=0;return "invalid";} //且得到的差的分子为负数,tagg=0 else return String.valueOf(cha); //否则直接返回差的分子部分 } //如果得到的差的分母不为1 if(cha<0){ //且差的分子部分为负数 tagg=0; //则tagg=0 return "invaild"; }else if(cha==0){ //如果在差的分母不为1的情况下分子为0 return "0"; //则返回字符串0 }else{ //如果差的分母不为1,且分子大于0 int z=cha/rfm; //尝试将得到的差化为真分数的形式 if(z==0){ return cha+"/"+rfm; }else{ int rfz=cha-z*rfm; if(rfz==0) return String.valueOf(z); else return z+"‘"+rfz+"/"+rfm; } } } public String fmulf(String s1,String s2){ //实现两个分数相乘 String[] s11=s1.split("/"); //分别获得两个分数的分子分母 String sfz1=s11[0]; String sfm1=s11[1]; String[] s22=s2.split("/"); String sfz2=s22[0]; String sfm2=s22[1]; int fz1=Integer.parseInt(sfz1); int fm1=Integer.parseInt(sfm1); int fz2=Integer.parseInt(sfz2); int fm2=Integer.parseInt(sfm2); int z=fz1*fz2; //分子相乘 int fm=fm1*fm2; //分母相乘 int y=z/fm; if(fm==1)return String.valueOf(z); //如果积的分母部分为1,则直接返回分子部分 if(z==0){ //如果积的分子为0,则直接返回字符串0 return "0"; }else if(y==0){ //如果不符合以上两种情况,则将得到的积转化为规定的真分数的形式 return z+"/"+fm; }else{ int fz=z-y*fm; if(fz==0)return String.valueOf(y); else return y+"‘"+fz+"/"+fm; } } public String fdevf(String s1,String s2){ //实现两个分数相除 String[] s11=s1.split("/"); //分别获得两个分数的分子分母 String sfz1=s11[0]; String sfm1=s11[1]; String[] s22=s2.split("/"); String sfz2=s22[0]; String sfm2=s22[1]; int fz1=Integer.parseInt(sfz1); int fm1=Integer.parseInt(sfm1); int fz2=Integer.parseInt(sfz2); int fm2=Integer.parseInt(sfm2); if(fz2==0){tagg=0;return "invalid";} //如果第二个分数为0,tagg=0 if(fz1==0)return "0"; //如果第一个分数的分子为0,则直接返回字符串0 String d1=s1; //否则,第一个分数保持不变 String d2=fm2+"/"+fz2; //第二个分数转化为其倒数 return fmulf(d1,d2); //除运算转变为乘运算 } }
3.查重
public class check1{ option oo=new option(); int []fhs=new int[10000]; //放有效符号个数的字符串数组 String por=""; int cc=1; //全局变量控制check2 int c=0; int tag5=1; //标记表达式属不属于有效表达式 public check1(int i,expression exp1,String []bds) { int k=i; //用户规定的表达式的个数 String b=exp1.expression1; //当前 产生的表达式 int d=exp1.fhnum; //当前产生的表达式的符号个数 String e=oo.ZTH(b); //调用ZTH()将当前生成的表达式转换为后缀表达式 String []e1=e.split(" "); //将后缀表达式用空格分割放入字符串数组 int e12=e1.length-1; String []e13=new String[e12]; for(int e14=0;e14<e13.length;e14++) { //去掉后缀表达式最前面的空格 e13[e14]=e1[e14+1]; } List<TreeNode> list1=buildtree(e13); //将后缀表示式转换为二叉树并返回广度搜索后的结点列表 for(c=0;c<k;c++) { if(bds[c]==null) break; //当有效表达式数组为空时 if((fhs[c])==d) { //先判断符号个数,当符号个数相同时,进行查重 String e2=oo.ZTH(bds[c]); //调用后缀函数获取后缀表达式 String []e21=e2.split(" "); int e23=e21.length-1; String []e22=new String[e23]; for(int e24=0;e24<e22.length;e24++) { e22[e24]=e21[e24+1]; } List<TreeNode> list2=buildtree(e22); //记录有效表达式的结点列表,作为后续查重比较的参照对象 List<TreeNode> list3=buildtree(e22); List<TreeNode> list4=buildtree(e22); List<TreeNode> list5=buildtree(e22); List<TreeNode> list6=buildtree(e22); List<TreeNode> list7=buildtree(e22); List<TreeNode> list8=buildtree(e22); List<TreeNode> list9=buildtree(e22); List<TreeNode> list10=buildtree(e22); List<TreeNode> list11=buildtree(e22); List<TreeNode> list12=buildtree(e22); List<TreeNode> list13=buildtree(e22); List<TreeNode> list14=buildtree(e22); List<TreeNode> list15=buildtree(e22); boolean ch=check2(list1,list2,list3,list4,list5,list6,list7,list8,list9,list10,list11,list12,list13,list14,list15); if(ch==false) { tag5=0; break;} //如果当前表达式与有效表达式重叠,则舍弃并推出循环 } } if (tag5==1) { //如果不重叠,将当前表达式写入有效表达式数组 bds[c]=b; } } public List<TreeNode> buildtree(String []o) { //将后缀表达式转换为二叉树,返回广度搜索后的结点列表 Stack<TreeNode> stack=new Stack<TreeNode>(); List<TreeNode> nodelist=new ArrayList<TreeNode>(); Queue<TreeNode> myQueue=new LinkedList<TreeNode>(); List<TreeNode> myQueue1=new ArrayList<TreeNode>(); TreeNode root=new TreeNode(" "); for(int i=0;i<o.length;i++) //将后缀表达式转换为二叉树 { if(o[i].equals("+")||o[i].equals("-")||o[i].equals("*")||o[i].equals("÷")) { root=new TreeNode(o[i]); root.right=stack.pop(); root.left=stack.pop(); stack.push(root); } else { stack.push(new TreeNode(o[i])); } } ((LinkedList<TreeNode>) myQueue).add(root); //广度搜索二叉树,记录广度搜索二叉树后的结点列表 while(!myQueue.isEmpty()) { TreeNode node=myQueue.poll(); myQueue1.add(node); if(null!=node.left) { ((LinkedList<TreeNode>) myQueue).add(node.left); } if(null!=node.right) { ((LinkedList<TreeNode>) myQueue).add(node.right); } } return myQueue1; } public boolean check2(List<TreeNode> list1,List<TreeNode> list2,List<TreeNode> list3,List<TreeNode> list4,List<TreeNode> list5,List<TreeNode> list6,List<TreeNode> list7,List<TreeNode> list8,List<TreeNode> list9,List<TreeNode> list10,List<TreeNode> list11,List<TreeNode> list12,List<TreeNode> list13,List<TreeNode> list14,List<TreeNode> list15) { //利用蛮力法查重 int []addr=new int[3]; int num=0; por=""; postOrderRe(list1.get(0)); String list1por=por; for(int r=0;r<list2.size();r++) { if(list2.get(r).val=="+"||list2.get(r).val=="*") { addr[num]=r; //记录列表中“+”或“*”的树节点的位置 num++; //记录列表中“+”或“*”的个数 } } //根据列表中“+”或“*”的个数,分析相应的情况 if(num==0) { //如果无+或*,则直接比较后缀表达式,若相同则重叠 por=""; postOrderRe(list2.get(0)); String list2por=por; if(list1por.equals(list2por)) return false; else return true; } if(num==1) { //如果无+或*的个数为1,则根据+或*的位置,获取其另一个同构的二叉树,转换成后缀表达式后与有效表达式的后缀比较,若相同则重叠 TreeNode trn; por=""; postOrderRe(list2.get(0)); String listpor2=por; if(list1por.equals(listpor2)) return false; //将当前表达式的后缀表达式与有效表达式的后缀表达式比较,若相同则重叠 trn=list3.get(addr[0]).left; //若不同,调换“+”或“*”位置的结点的左右子树,再判断,若相同则重叠 list3.get(addr[0]).left=list3.get(addr[0]).right; list3.get(addr[0]).right=trn; por=""; postOrderRe(list3.get(0)); String listpor3=por; if(list1por.equals(listpor3)) return false; else return true; } if(num==2) { /*如果+或*的个数为2,则根据+或*的位置,分别获取另外三种与其同构的二叉树,加上原本的有效表达式,一共四种情况, 分别转换成后缀表达式后与当前表达式的后缀比较,若相同则重叠*/ List<TreeNode> l3=new ArrayList<TreeNode>(); List<TreeNode> l4=new ArrayList<TreeNode>(); List<TreeNode> l5=new ArrayList<TreeNode>(); List<TreeNode> l6=new ArrayList<TreeNode>(); l3=list4; l4=list5; l5=list6; l6=list7; TreeNode trn4,trn5,trn6,trn7; por=""; postOrderRe(l3.get(0)); String listpor3=por; if(list1por.equals(listpor3)) return false; trn4=l4.get(addr[0]).left; l4.get(addr[0]).left=l4.get(addr[0]).right; l4.get(addr[0]).right=trn4; por=""; postOrderRe(l4.get(0)); String listpor4=por; if(list1por.equals(listpor4)) return false; trn5=l5.get(addr[1]).left; l5.get(addr[1]).left=l5.get(addr[1]).right; l5.get(addr[1]).right=trn5; por=""; postOrderRe(l5.get(0)); String listpor5=por; if(list1por.equals(listpor5)) return false; trn6=l6.get(addr[0]).left; l6.get(addr[0]).left=l6.get(addr[0]).right; l6.get(addr[0]).right=trn6; trn7=l6.get(addr[1]).left; l6.get(addr[1]).left=l6.get(addr[1]).right; l6.get(addr[1]).right=trn7; por=""; postOrderRe(l6.get(0)); String listpor6=por; if(list1por.equals(listpor6)) return false; return true; } if(num==3) { /*如果+或*的个数为3,则根据+或*的位置,分别获取另外七种与其同构的二叉树,加上原本的有效表达式,一共八种情况, 分别转换成后缀表达式后与当前表达式的后缀比较,若相同则重叠*/ List<TreeNode> l7=new ArrayList<TreeNode>(); List<TreeNode> l8=new ArrayList<TreeNode>(); List<TreeNode> l9=new ArrayList<TreeNode>(); List<TreeNode> l10=new ArrayList<TreeNode>(); List<TreeNode> l11=new ArrayList<TreeNode>(); List<TreeNode> l12=new ArrayList<TreeNode>(); List<TreeNode> l13=new ArrayList<TreeNode>(); List<TreeNode> l14=new ArrayList<TreeNode>(); l7=list8; l8=list9; l9=list10; l10=list11; l11=list12; l12=list13; l13=list14; l14=list15; TreeNode trn8,trn9,trn10,trn11,trn12,trn13,trn14,trn15,trn16,trn17,trn18,trn19; por=""; postOrderRe(l7.get(0)); String listpor7=por; if(list1por.equals(listpor7)) return false; trn8=l8.get(addr[0]).left; l8.get(addr[0]).left=l8.get(addr[0]).right; l8.get(addr[0]).right=trn8; por=""; postOrderRe(l8.get(0)); String listpor8=por; if(list1por.equals(listpor8)) return false; trn9=l9.get(addr[1]).left; l9.get(addr[1]).left=l9.get(addr[1]).right; l9.get(addr[1]).right=trn9; por=""; postOrderRe(l9.get(0)); String listpor9=por; if(list1por.equals(listpor9)) return false; trn10=l10.get(addr[2]).left; l10.get(addr[2]).left=l10.get(addr[2]).right; l10.get(addr[2]).right=trn10; por=""; postOrderRe(l10.get(0)); String listpor10=por; if(list1por.equals(listpor10)) return false; trn11=l11.get(addr[0]).left; l11.get(addr[0]).left=l11.get(addr[0]).right; l11.get(addr[0]).right=trn11; trn12=l11.get(addr[1]).left; l11.get(addr[1]).left=l11.get(addr[1]).right; l11.get(addr[1]).right=trn12; por=""; postOrderRe(l11.get(0)); String listpor11=por; if(list1por.equals(listpor11)) return false; trn13=l12.get(addr[0]).left; l12.get(addr[0]).left=l12.get(addr[0]).right; l12.get(addr[0]).right=trn13; trn14=l12.get(addr[2]).left; l12.get(addr[2]).left=l12.get(addr[2]).right; l12.get(addr[2]).right=trn14; por=""; postOrderRe(l12.get(0)); String listpor12=por; if(list1por.equals(listpor12)) return false; trn15=l13.get(addr[1]).left; l13.get(addr[1]).left=l13.get(addr[1]).right; l13.get(addr[1]).right=trn15; trn16=l13.get(addr[2]).left; l13.get(addr[2]).left=l13.get(addr[2]).right; l13.get(addr[2]).right=trn16; por=""; postOrderRe(l13.get(0)); String listpor13=por; if(list1por.equals(listpor13)) return false; trn17=l14.get(addr[0]).left; l14.get(addr[0]).left=l14.get(addr[0]).right; l14.get(addr[0]).right=trn17; trn18=l14.get(addr[1]).left; l14.get(addr[1]).left=l14.get(addr[1]).right; l14.get(addr[1]).right=trn18; trn19=l14.get(addr[2]).left; l14.get(addr[2]).left=l14.get(addr[2]).right; l14.get(addr[2]).right=trn19; por=""; postOrderRe(l14.get(0)); String listpor14=por; if(list1por.equals(listpor14)) return false; return true; }return true; } public void postOrderRe(TreeNode biTree) { //后序遍历二叉树,将二叉树转换为后缀表达式 if(biTree!=null) { postOrderRe(biTree.left); postOrderRe(biTree.right); por+=biTree.val; } } }
六、测试运行
1.expression模块测试
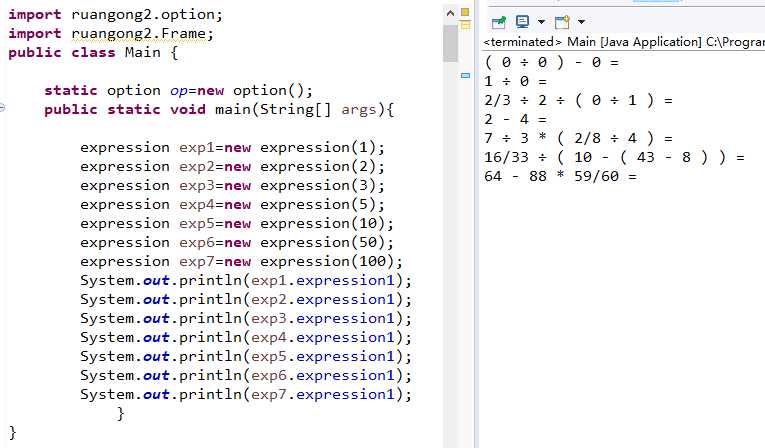
2.option模块测试
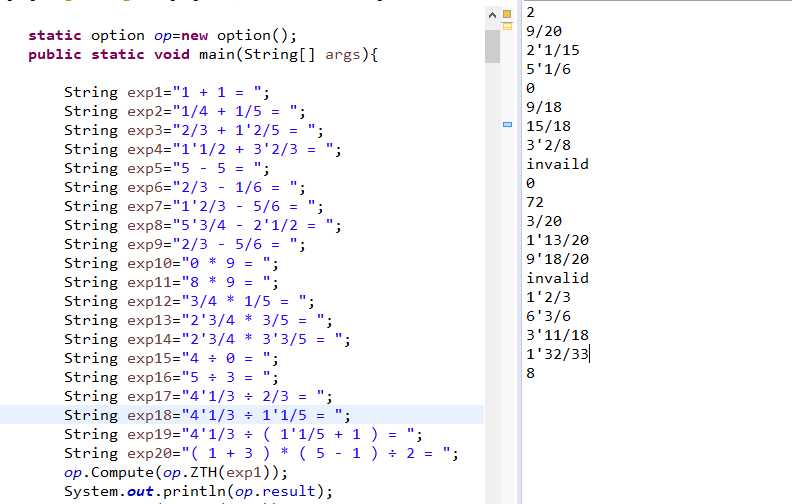
3.check模块测试
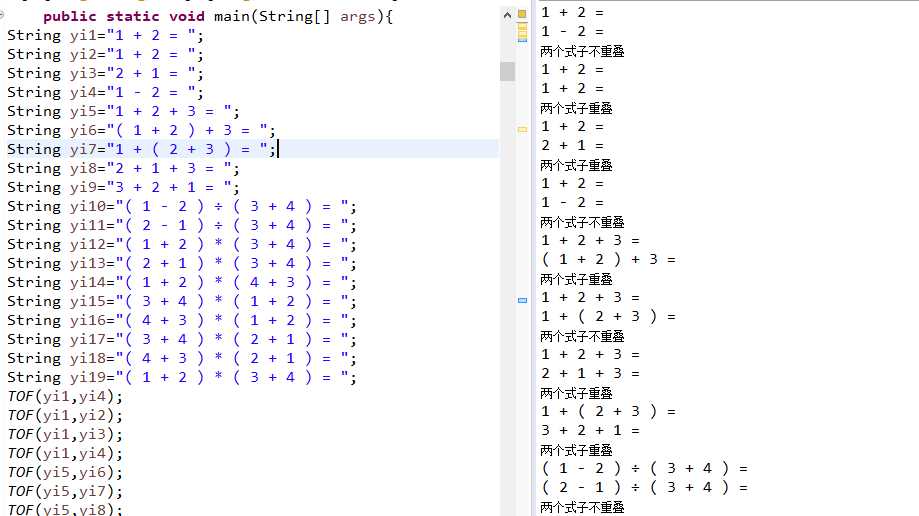

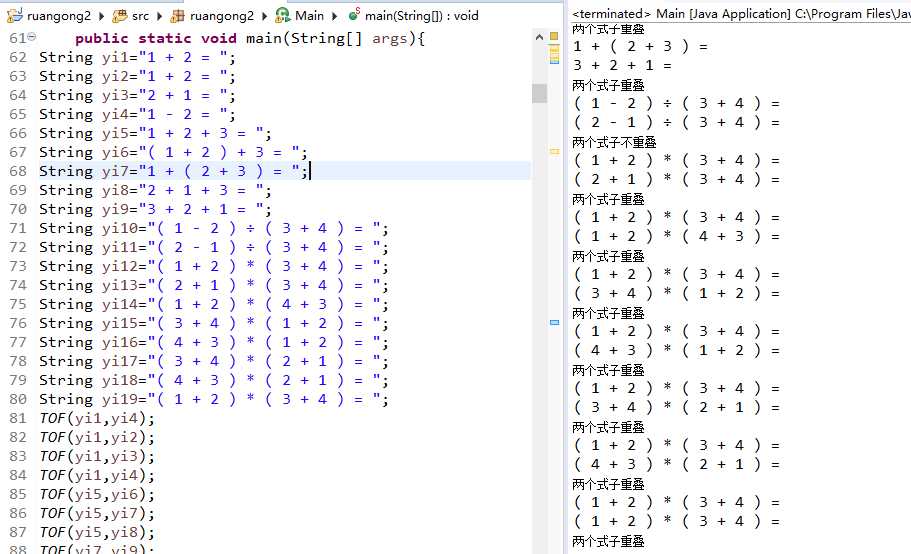
4.用户界面
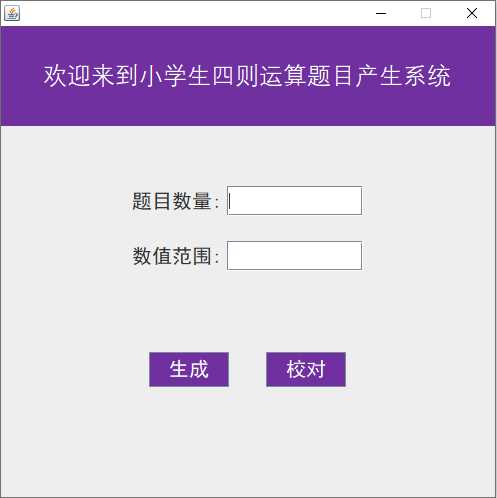
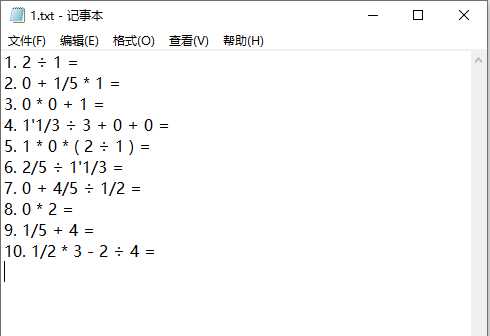
5.生成题目文件
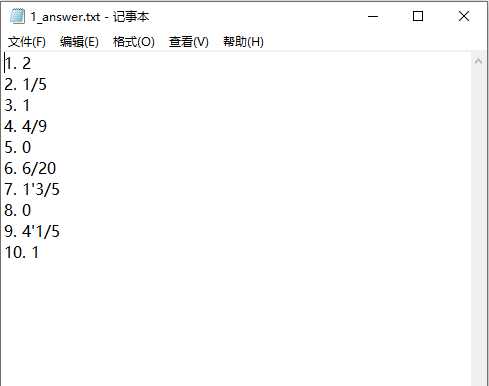
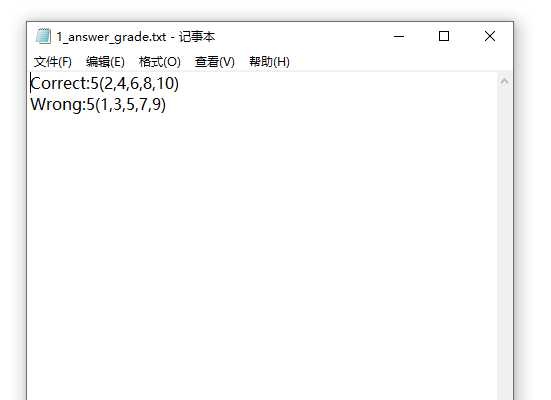
7.校对功能
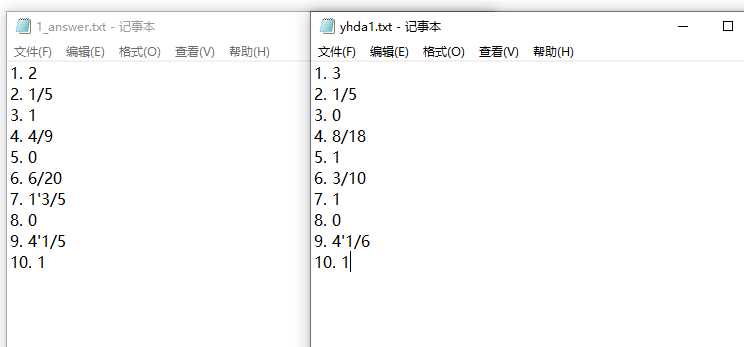
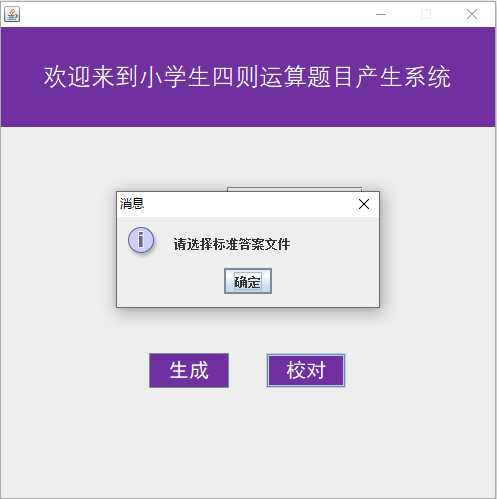
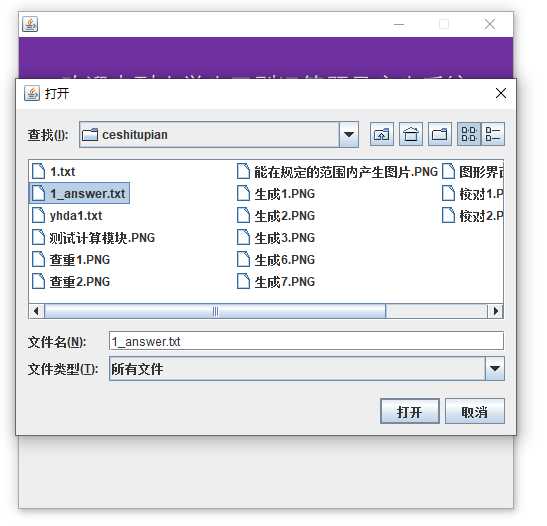
七、遇到的困难及解决办法
1.产生表达式时,需要考虑在表达式中随机生成括号的问题。一开始我们考虑首先在表达式中利用随机数控制左括号在有效区域放置并记录放置位置,然后再通过判断左括号的个数随机在右括号有效区域内放置右括号。这样的生成括号方式虽然能够产生有括号的表达式,但是我们发现它会产生无效的括号对,比如在仅有一个运算符的表达式中增加括号,以及给一整个表达式增加括号。为了解决这个问题,针对本次相项目,由于给定最多一个表达式中只允许放3个运算符,因此我们列举了括号的放置情况,发现最多情况下只有10种情况。因此我们利用几个随机数分别控制括号对的数量以及括号对的位置,确定表达式。这样做省去了判断左右括号是否对应以及避免了一些无效增加括号对的情况。不足之处在于如果运算符增加,情况会增加无法一一列举。
2.查重是整个项目耗时最长的模块。我们一开始发现两个表达式有效变换的形式有很多种,要判断每一种情况下表达式是否重叠十分的复杂。也花了较长的时间去理解清楚两个表达式为什么会重叠。最后发现原因是+或*有交换律,÷或*则没有,当我们将中缀表达式经过后缀表达式转换为二叉树时,只有树节点为+或*的才可以调换其左右子树从而产生其同构树,即表明+或*的左右表达式在运算上没有优先级之分。我们最初采用逐步缩小查重范围的方式,首先利用正则表达式判断需要比较的两个表达式的符号个数是否相同,如果相同,再判断数值是否相同,排除掉符号个数不同或数值不同的表达式,进入最终的比较,采取逐一比较树结构的结点,若同层同一边子树树节点不同则调换左右结点再重新判断,调换完如果相同就继续遍历直到遍历完整棵树的结点。但是在后来的思考过程中,我们发现,这种情况下需要在每一层遇到运算符为÷或-的时候,不允许调换左右结点。并且需要考虑+和*也需要调换左右结点。情况十分复杂。也是我们遭遇的瓶颈。为了解决这个问题,我们重新分析当前的表达式,我们利用最原始的方式,发现可以仅判断+或*的个数,记录+或*在式子中出现的位置,因为+或*两边的结点调换是可以列出所有的情况的,并且情况之间都是由规律的。因此我们采取了蛮力法,将当前表达式的二叉树所有同构二叉树都列举出来并分别写出后缀表达式与有效表达式的后缀表达式比较。如果相同,表示重叠。虽然实现查重的过程中使用了蛮力法,但是由于每种情况下需要写的代码都将近一致,所以其实不算复杂。并且能够较为直观的将表达式的所有同构写出来。最终我们完美的实现了查重功能。
3.校对文件。我们在校对答案时考虑了一个问题。如果答案是分数但是由于分数可以不是最简形式那怎么办呢。这样情况下,即使用户输入正确的结果,但是由于同一个数值用分数表示可以有不同的形式,所以可能会导致即使数值对了但是也会因为“长得不一样”而判错。我们根据这个问题开始思考,那么必须让数值一样形式不一样的也能匹配到相同啊!最后我们想到,如果数值相同的话,两个数值相减肯定为0,如果运用减法运算就完全不用考虑形式的问题了!因此我们调用option模块里两个数值相减的函数fminusf()去将结果相减后校对。最终成功校对了,实现了校对功能。
八、项目小结
本次结对项目,我们两个人首先一起分析了题目,确定了代码的实现所需要的模块以及框架。在分析清楚的基础上分配代码任务,规定了每日的计划以及总的任务进度表。完成了基本的代码后,我们一起对各个模块进行测试,确定各个模块均能够独立实现之后,对接模块之间的接口以及调用关系。将代码整合,构成整个程序。在撰写博客上,我们分工合作,逐步完成功能测试,PSP表,博客撰写以及效能分析等。总的来说,此次结对项目我们分工有序,遇到问题时先独立解决后寻求队友帮助,一起解决问题。在进行各自的代码任务时保持联系,了解双方进度从而确保任务进度。共同完成整个项目,是一个十分愉快而且收获很大的合作经历。
我们在本次结对编程中有一个不足之处在于,由于我们模块代码是分开两台电脑写的,在原先开始编码时,我们没有留意到双方电脑编码格式的问题,没有做统一的规范,导致最后在传代码时出现了中文乱码的情况,比较难解决。这是一个教训也是一个经验,在往后的合作项目中,我们都会注意这个问题。
这次结对编程收获很大,我们意识到了两个人合作的话可以在遇到不懂的时候共同讨论问题,在讨论中碰撞思想,更容易解决问题。平常一个人想的时候可能有时候会由于当局者迷的原因,而忽略了一下因素导致问题的死循环。但是两个人一起讨论一起面对问题的时候,能够看出对方思想的漏洞及时提出,及时止损,促进了项目完成的进度。另外我们发现两个人共同分析并制定并通过互相了解进度是十分有必要而且有效的,双方先确定总体框架一致,在逐步完善框架,是一个十分有趣而且锻炼的过程。我们在完成此次项目的过程中,在双方身上都发现了自己值得学习的地方。总而言之,这是一个很棒的体验。
标签:return invalid result tar kth 块代码 des 否则 结构
原文地址:https://www.cnblogs.com/clarazhang/p/11689444.html