标签:|| 源码 这一 相同属性 case 修改 描述 creat 清华大学
红黑树是一种特殊的平衡二叉树(AVL),可以保证在最坏的情况下,基本动态集合操作的时间复杂度为O(logn)。因此,被广泛应用于企业级的开发中。
在一棵红黑树中,其每个结点上增加了一个存储位(属性color)来表示结点的颜色,且颜色只能是red or black。通过对任何一条从根到叶子的简单路径上各个结点的颜色进行约束,红黑树确保没有一条路径会比其他路径长出2倍,因而是近似于平衡的。
树中每个结点包含5个属性:color、val、lchild、rchild和p(可选)。如果一个结点没有子结点或父结点,则该结点相应指针属性的值为NIL。我们可以把这些NIL视为指向二叉搜索树的叶结点(外部结点)的指针,而把带关键字的结点视为树的内部结点。
一棵红黑树是满足下面红黑性质的二叉搜索树:
为了便于处理红黑树代码中的边界条件,使用一个哨兵来代表NIL。对于一棵红黑树tree,哨兵NIL是与一个与树中普通结点有相同属性的对象。它的color属性为black,其他属性可以为任意值。
在一棵含有n个关键字的红黑树上,进行插入和删除操作,需要的时间复杂度为O(logn),由于这两个操作,会导致插入和删除后的树不满足红黑树的性质。为了维护这些性质,需要改变树中某些结点的颜色以及指针结构。
指针结构的修改是通过旋转来完成的,这是一种能保持二叉搜索树性质的搜索树局部操作,旋转分为左旋和右旋。如下图所示:

下面给出左旋和右旋操作的代码为:
1 template<typename T> 2 void RedBlackTree<T>::LeftRotation(RedBlackNode<T>* &t){ 3 RedBlackNode<T> *temp = t->rchild; 4 t->rchild = temp->lchild; 5 if(Parent(t)==NIL){ 6 root = temp; 7 } 8 temp->lchild = t; 9 Parent(t)->rchild = temp; 10 } 11 12 template<typename T> 13 void RedBlackTree<T>::RightRotation(RedBlackNode<T>* &t){ 14 RedBlackNode<T> *temp = t->lchild; 15 t->lchild = temp->rchild; 16 if(Parent(t)==NIL){ 17 root = temp; 18 } 19 temp->rchild = t; 20 Parent(t)->lchild = temp; 21 }
左旋和右旋的伪码可以参考《算法导论》(砖头书)。
前面说过,在一棵含有n个关键字的红黑树上,执行插入操作,需要时间复杂度为O(logn)。为了做到这一点,需要往原红黑树中插入一个红色的结点。那么问题来了,为什么插入的是红色结点,而不是黑色结点呢?我们知道,红黑树有五个性质,如果插入红色结点,则可能会违反性质4,而如果是插入黑色结点,则一定会违反性质5。也就是说,插入红色结点比插入黑色结点更不容易违反红黑树的性质,而违反性质条数越多,相应的要做的调整操作也就越多,导致算法的时间复杂度也就越高,从而影响算法的执行速度。在《数据结构算法与解析》(高一凡著,清华大学出版社)一书中,给出了插入结点为红色以及插入结点为黑色两种操作的算法,本文以插入结点为红色进行讲解。
对于一棵红黑树来说,插入一个红色结点,主要有六种情况,其中三种与另外三种是对称的。这一点取决于插入结点 z 的父亲结点是插入结点的祖父结点的左孩子还是右孩子。
下面给出两种对称下,所对应的三种情况:

上图显示了该情况的情形,这种情况实在插入结点z的父结点z.p和其叔结点y都是红色时发生的。因为插入结点z的祖父结点z.p.p是黑色的,所以将z.p和y都着为黑色,来解决z和z.p都是红色的问题,而由于性质5的要求,如果只是把z.p和y的颜色改为黑色,则会破坏该性质,因此需要对z.p.p结点的颜色进行调整,以保证性质5的满足。
但是,性质1调整以后,就一定能维持红黑树的性质吗?我们以z表示新插入的结点,z‘表示经过此次操作后的结点,由上述操作可以知道,z‘=z.p.p。则经过此次操作后,有以下结果:
如果结点z‘在下一次操作开始时是根结点,则在这次操作中case1修正了唯一被破坏的性质4。由于z‘是红色的而且是根结点,所以性质2成为唯一被违反的性质,这是由z‘导致的。
如果结点z‘在下一次操作开始时不是根结点,则case1不会导致性质2被破坏,case1修正了在这次操作的开始唯一违反的性质4。然后把z’着色为红色而z‘.p不变,因此,如果z‘.p是黑色的,则没有违反性质4,若是z‘.p是红色的,则违反了性质4。
在case2和case3中,z的叔结点是黑色的。通过z是z.p的右孩子还是左孩子来区别这两种情况(叔结点都是黑色,无法在逻辑上进行区别)。对于这两种情况,如下图所示:

左图为case2,右图为case3
我们发现case2与case3存在某种指针结构上的关系,很明显二者之间可以通过左旋和右旋操作进行相互转换。由于z和z.p都是红色的,因此,旋转操作对树的黑高和性质5都无影响。无论怎么进入哪两种情况,y总是黑色的,否则就要执行case1对应的操作。此外,这种旋转操作,有个好处是,并不改变旋转后,z的身份,尽管会导致z的左右孩子身份改变了,但依旧是z.p的孩子。在case3中,我们可以通过改变某些结点的颜色,并作一次右旋,就能保证性质5。这样,由于在一行中不会再存在有两个红色结点,因此,保证了红黑树的性质,所有的处理也到此完毕了。如下所示:
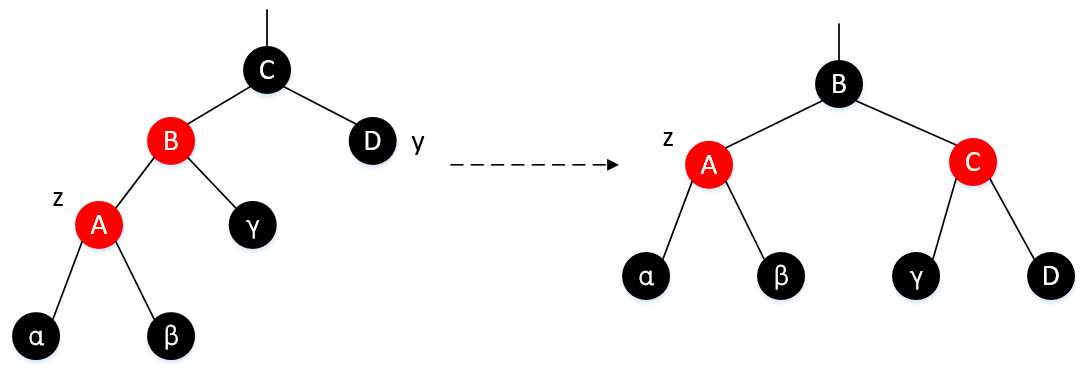
可以看到,case2和case3的操作,会最终使得插入结点后的树,维持红黑树的性质。由此,不禁怀疑,这样的操作能完全保证吗?答案是肯定的。下面来证明:
由于结点z在case2和case3中都不是根结点,因此,性质2未被破坏,这两种情况因此也不会引起性质2的违反。由此,证明了z.p为z.p.p的左孩子时候,对插入z后的红黑树,按照上述调整,可以做到恢复红黑树的性质。而当z.p为z.p.p的右孩子时,由于与前面一大情况是对称的,因此,通过修改left和right的对应,就可实现。而完全实现树的回复,可以通过while循环来保持。以下是实现树的插入的代码:
1 template<typename T> 2 bool RedBlackTree<T>::Insert(T e){ 3 RedBlackNode<T> *p, *f; 4 p = f = NULL; 5 6 if(!searchBST(root, p, e, f)){//not found, need to create, p points to the last node. 7 8 RedBlackNode<T> *s = createNewNode(e); 9 if(root==NULL){ 10 root = s; 11 root->color = "black"; 12 } 13 else{ 14 if(e<p->val){ 15 p->lchild = s; 16 } 17 else{ 18 p->rchild = s; 19 } 20 if(p->color == "red"){//double red node, need to adjust 21 adjustDoubleRed(s, p); 22 } 23 } 24 return true; 25 } 26 else{//node exists. return false 27 return false; 28 } 29 } 30 31 template<typename T> 32 RedBlackNode<T>* RedBlackTree<T>::Parent(RedBlackNode<T>* &t)const{ 33 /* 34 *@Parameter: 35 *q: a queue to save rb-node. 36 *t: a point which points to a node in the RBTree. 37 *father: a point which points to the father node of t. 38 */ 39 queue<RedBlackNode<T>*> q; 40 RedBlackNode<T>* father; 41 if(root!=NULL){ 42 q.push(root); 43 while(!q.empty()){//BFSTraverse to find the father node of t. 44 father = q.front(); 45 q.pop(); 46 if((father->lchild!=NIL&&father->lchild==t)||(father->rchild!=NIL&&father->rchild==t)){ 47 return father; 48 } 49 else{ 50 if(father->lchild!=NIL){ 51 q.push(father->lchild); 52 } 53 if(father->rchild!=NIL){ 54 q.push(father->rchild); 55 } 56 } 57 } 58 } 59 return NIL; //not found, return NIL 60 } 61 62 template<typename T> 63 bool RedBlackTree<T>::searchBST(RedBlackNode<T>* &t, RedBlackNode<T>* &p, T &e, RedBlackNode<T>* f)const{ 64 //在树中t中递归地查找其值等于e的数据,若查找成功,则指针p指向该数据 65 //结点,并返回true,否则指针p指向查找路径上访问的最后一个结点以便插入 66 //并返回false,指针f指向p的双亲,其初始调用值为NULL。Insert()调用 67 if(t==NULL||t==NIL){ 68 p = f; 69 return false; 70 } 71 if(e==t->val){ 72 p = t; 73 return true; 74 } 75 else if(e<t->val){ 76 return searchBST(t->lchild, p, e, t); 77 } 78 else{ 79 return searchBST(t->rchild, p, e, t); 80 } 81 } 82 83 template<typename T> 84 void RedBlackTree<T>::LeftRotation(RedBlackNode<T>* &t){ 85 RedBlackNode<T> *temp = t->rchild; 86 t->rchild = temp->lchild; 87 if(Parent(t)==NIL){ 88 root = temp; 89 } 90 temp->lchild = t; 91 Parent(t)->rchild = temp; 92 } 93 94 template<typename T> 95 void RedBlackTree<T>::RightRotation(RedBlackNode<T>* &t){ 96 RedBlackNode<T> *temp = t->lchild; 97 t->lchild = temp->rchild; 98 if(Parent(t)==NIL){ 99 root = temp; 100 } 101 temp->rchild = t; 102 Parent(t)->lchild = temp; 103 } 104 105 template<typename T> 106 void RedBlackTree<T>::adjustDoubleRed(RedBlackNode<T>* &s, RedBlackNode<T>* &p){ 107 /* 108 *@Parameter: 109 *s: rb-node. 110 *p: the father node of s. 111 */ 112 RedBlackNode<T> *y, *gp; 113 while(p->color=="red"){ 114 gp = Parent(p); 115 if(p==gp->lchild){ 116 y = gp->rchild; 117 if(y->color=="red"){//case 1 118 p->color = "black"; 119 y->color = "black"; 120 gp->color = "red"; 121 s = gp; 122 p = Parent(s); 123 } 124 else if(s==p->rchild){//case 2 125 s = p; 126 LeftRotation(p); 127 } 128 else{ 129 p->color = "black"; 130 gp->color = "red"; 131 RightRotation(gp); 132 } 133 } 134 else{ 135 y = gp->lchild; 136 if(y->color=="red"){//case 1 137 p->color = "black"; 138 y->color = "black"; 139 gp->color = "red"; 140 s = gp; 141 p = Parent(s); 142 } 143 else if(s==p->lchild){//case 2 144 s = p; 145 RightRotation(s); 146 } 147 else{ 148 p->color = "black"; 149 gp->color = "red"; 150 LeftRotation(gp); 151 } 152 } 153 } 154 root->color = "black"; 155 }
代码的操作,与前文图片所描述的操作相一致。
由于红黑树与BST树相似,因此,其删除操作与BST树在逻辑上是基本一致的,唯一的区别在于,红黑树需要对删除结点后的树进行调整,使其符合红黑树的性质。对于一棵红黑树来说,如果先不考虑结点的颜色,删除一个结点无非是三种情况,这一点与BST树是一致的,即:
根据上述三种情况,可以编写出BST树的删除结点操作的代码,下面给出BST树的删除操作示意图:



很明显,红黑树在结点的结构上,也是符合上述形式的,即左<根<右,因此,红黑树的删除操作是从BST输的删除操作的基础上,修改得到的,为什么需要修改呢?就是因为红黑树的每个结点具有红黑属性。
由于红黑属性的影响,导致,删除结点后红黑树将不符合红黑树原有的特性,我们知道,删除某个结点,按照上述调整,将会使得被删除结点所在的子树不符合原红黑树的特性1、2、4或5(非删除结点不受影响)。因此,只需要对子树进行颜色调整,就能使红黑树性质保持不变。
如何删除的原理已经讲明白了,那么我们看,两个结点是如何替换(也就是发生删除操作的)。

在伪码中,结点u为被替换结点,你可以理解为,被删除结点,而v是用来替换被删除结点的结点(通常为u的子节点或者u的右子树结点的最小节点)。
下面是我实现的transplant函数:
1 template<typename T>
2 void RedBlackTree<T>::Transplant(RedBlackNode<T>* &u, RedBlackNode<T>* &v){
3 /*
4 *a function to achieve node u is replaced by v.
5 *@Parameter:
6 *u: a node which is replaced by v.
7 *v: a node wants to replace u.
8 */
9 if(Parent(u) == NIL){//待删除结点为根结点.
10 root = v;
11 }
12 else if(u==Parent(u)->lchild){
13 Parent(u)->lchild = v;
14 }
15 else{
16 Parent(u)->rchild = v;
17 }
18 }
下面给出删除操作的伪代码(源自《算法导论》)。

在上述代码中,结点z为删除结点,y为指向结点z的指针。我们知道,BST的删除操作是很容易实现的,对于红黑树来说,关键在于,删除操作以后,什么情况下,会破坏红黑树的红黑性质。
由于y的颜色有可能发生改变(因为根据代码,y始终指向树结构中被删除结点的位置),用变量y_original_color存储了发生改变前的y位置的颜色。第2行和第10行在给y赋值之后,立即设置该变量。当z有两个子结点时,则y!=z且结点y移至红黑树中结点z的原始位置;第20行给y赋予和z一样的颜色。然后保存y的原始颜色,以在删除操作结束时,测试它;如果它是黑色的,那么删除或移动y会引起红黑性质的破坏,为什么会是黑色引起红黑性质的破坏呢?

如上图所示,如果删除结点5,对于左侧的树,如果删除结点y,则结点7不会违反任何红黑树的性质,因为结点y的子结点为必定为黑色(由于红黑树的性质),因此,y为红色不会引起红黑树性质的改变;对于右侧的树,如果删除结点y,则如果结点y的子结点为NIL(黑色),不会引起结点7与结点y子结点之间都为红色,从而不违反了红黑树的性质。

从左边的红黑树来看,如果待删除结点颜色为黑色,当对该结点进行操作时,则由于,其子结点为红色,与y结点的父结点同为红色,因此,会违背红黑树的性质,而如果是右边的情况,则不会,因为删除结点y以后,由于结点4依旧为黑色,不会破坏红黑树的性质。对于这种情况下,左子树结点不存在而右子树结点存在的情况,也是同样的道理,读者可以自己画图思考一下。
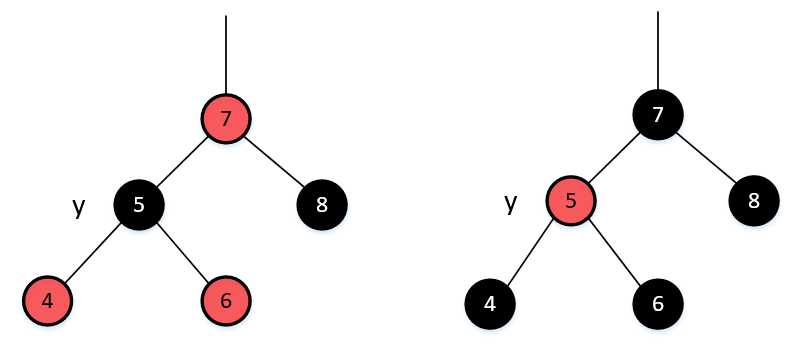
从上图来看,如果删除结点5,会与情况2一样而违反性质,而对于右边的树,则不会,因为,我们删除的方式,是将z结点也就是结点5的左子树,连接到结点5右子树的值最小的结点上。然后用这个最小结点来替换原来结点z(也就是图上结点5的位置)。这样做的好处是,仍可以保证删除后的树仍满足BST树的性质,我们只需要对被删除结点的子树进行修改颜色性质就可以了,而且,不论最小结点的颜色如何,都不会导致出现两个红结点的情况。这一点可能很多人会存在疑惑,我们来分析一下:
对于左右子树都存在的的删除结点来说,此时,y从指向z转向了指向删除结点z的右子树种最小的一个结点(右子树的最左结点),这样的指向,无非两种情况,一种是右子树的最左结点就是被删除结点z的右孩子,即其右孩子的左孩子为NIL,这样,以上右图为例,y指向了结点6,然6后,用y_original_color来保存结点6的颜色,用x指向6的右孩子,由于在这里,y的父亲结点依旧为删除结点z,因此,设置好结点属性x.p = y,然后,执行替换操作(Transplant)来实现删除的目的,可以看到,transplant操作是对删除结点z和替换结点y进行操作的,对于这种情况来说,是将z与其右孩子进行替换,根据伪码,结点7的左孩子指向了结点6。然后结点6也就是现在的结点y的左孩子指向了结点z的左孩子,这样就完成了然后将结点y的颜色,改成结点z的颜色,为什么这么做呢,是为了保持与原来红黑树相同的特性,因为我们知道,在删除结点5之前,结点5左右两棵子树的一条路径上的黑色结点数目是相同的,但是,由于结点6的上位(替换了其父结点),而父结点的左孩子直接成为其左子树,这就导致了左右两子树的不平衡,调整为与z结点相同的颜色以后,可以使得对红黑树修改操作仅局限于结点y这棵子树中进行。
另一种情况则是右子树的最左结点不是被删除结点z的右孩子,即其右孩子的左孩子非空,那么,其余操作不变,比较巧妙的是,这里运用了最左结点的左孩子为NIL的特性,将最左结点的右子树接到了其父节点的左边(这就保证了BST树的有序性),且这样的做法,使得该结点与树在结构上断开,无法通过树的根结点访问到,因此,后续再执行一次删除结点z与结点y的替换操作,就可以完成这样的删除操作。这种情况下,会产生y为红色或者黑色结点的问题,同样,也只会有黑色会违背红黑树的性质。
通过上面的分析,我们很容易得到这样的结论,那就是,只有当y为黑色结点的时候,才会发生违背红黑树性质的情况,因此,需要对这样的情况进行修改,来保持红黑树的性质。下面给出《算法导论》中,关于该操作的伪代码:

在分析源码以前,我们首先来分析,执行删除操作以后,会出现哪些违背红黑树性质的情况。在这个操作中,结合删除操作的代码,我们可以发现,x始终指向具有双重黑色的非根结点。那么,就会有4种情况,这四种情况与插入操作中的是类似的,请读者结合上述删除操作,自行分析。
下面附上红黑树删除操作的代码。
1 template<typename T> 2 void RedBlackTree<T>::Delete(RedBlackNode<T>* &t){ 3 /* 4 *function to delete node t in redblacktree. 5 *@Parameter: 6 *t: a node need to be deleted. 7 */ 8 RedBlackNode<T> *y; 9 RedBlackNode<T> *p; 10 y = t; 11 string y_original_color = y->color; 12 if(t->lchild==NIL){ 13 p = t->rchild; 14 Transplant(t, t->rchild); 15 } 16 else if(t->rchild==NIL){ 17 p = t->lchild; 18 Transplant(t, t->lchild); 19 } 20 else{ 21 y = TreeMinimum(t->rchild); 22 y_original_color = y->color; 23 p = y->rchild; 24 if(Parent(y)!=t){ 25 Transplant(y, y->rchild); 26 y->rchild = t->rchild; 27 } 28 Transplant(t, y); 29 y->lchild = t->lchild; 30 y->color = t->color; 31 } 32 33 if(y_original_color=="black"){ 34 RBDeleteFixup(p); 35 } 36 delete t; 37 t = NULL; 38 }
红黑树删除后,修改颜色的操作代码。
template<typename T> RedBlackNode<T>* RedBlackTree<T>::TreeMinimum(RedBlackNode<T>* t){ RedBlackNode<T> *p; while(t!=NIL){ p = t; t = t->lchild; } return p; } template<typename T> void RedBlackTree<T>::RBDeleteFixup(RedBlackNode<T>* &t){ RedBlackNode<T> *p; RedBlackNode<T> *f; while(t!=NIL&&t->color=="black"){ if(t==Parent(t)->lchild){ p = Parent(t)->rchild; if(p->color=="red"){ p->color = "black"; Parent(t)->color = "red"; f = Parent(t); LeftRotation(f); p = Parent(t)->rchild; } if(p->lchild->color=="black"&&p->rchild->color=="black"){ p->color = "red"; t = Parent(t); } else if(p->rchild->color=="black"){ p->lchild->color = "black"; p->color = "red"; RightRotation(p); p = Parent(t)->rchild; } else{ p->color = Parent(t)->color; Parent(t)->color = "black"; p->rchild->color = "black"; f = Parent(t); LeftRotation(f); t = root; } } else{ p = Parent(t)->lchild; if(p->color=="red"){ p->color = "black"; Parent(t)->color = "red"; f = Parent(t); RightRotation(f); p = Parent(t)->lchild; } if(p->rchild->color=="black"&&p->lchild->color=="black"){ p->color = "red"; t = Parent(t); } else if(p->lchild->color=="black"){ p->rchild->color = "black"; p->color = "red"; LeftRotation(p); p = Parent(t)->lchild; } else{ p->color = Parent(t)->color; Parent(t)->color = "black"; p->lchild->color = "black"; f = Parent(t); RightRotation(f); t = root; } } } t->color = "black"; }
标签:|| 源码 这一 相同属性 case 修改 描述 creat 清华大学
原文地址:https://www.cnblogs.com/sgatbl/p/9484097.html