标签:for info 实践 最大 for语句 分析 复杂度 运算 算法
1.实践题目
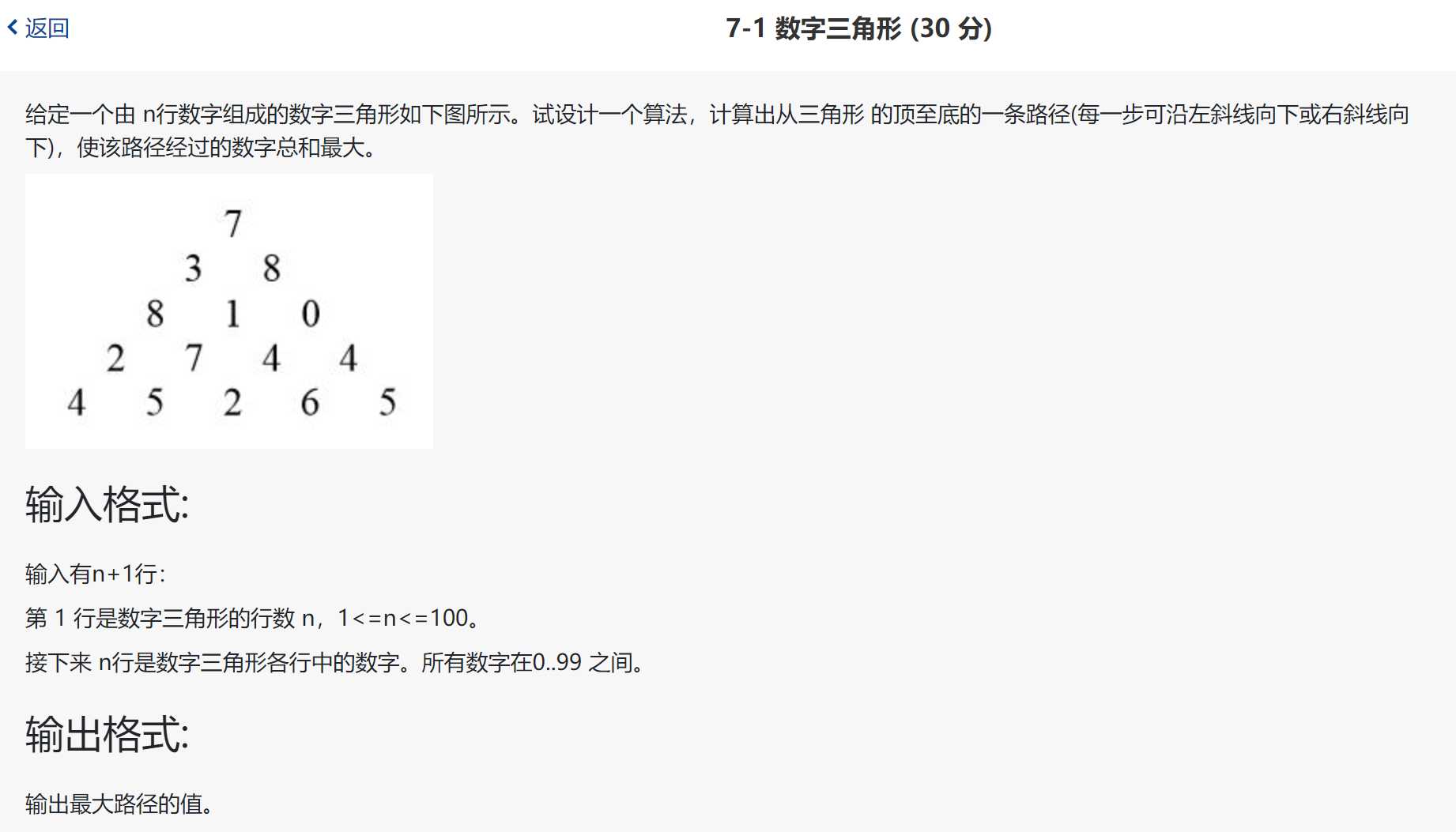
2.问题描述
设计一个算法,计算出从三角形 的顶至底的一条路径(每一步可沿左斜线向下或右斜线向下),使该路径经过的数字总和最大。
3.算法描述
定义一个二维数组a[][]存放各行各列的数字,再定义maxSum[i][j]二维数组用来存放从a[i][j]往下经过路径的数字最大和,则该题的解即为从上到下递归求maxSum[1][1]。再用备忘录方法,定义maxSum[][]所有值初值为-1,若已求过则该maxSum的值不为-1,这样可以把每个所求过的maxSum[][]都存下来,防止重复计算子问题。
过程如下,定义MaxSum函数为该递归的函数,函数内定义x为MaxSum[i+1][j],y为MaxSum[i+1][j+1](x为MaxSum[i][j]的左下方的最大数字和,y为右下方的最大数字和),从MaxSum[1][1]开始递归,设置判断如果maxSum不为-1,即之前计算过则直接返回该数值。
4.算法时间及空间复杂度分析
因为运用了备忘录方法,该数字三角形中数字总和为n(n+1)/2,该递归时间复杂度即为O(n²)
5.心得体会
一开始没有用备忘录方法,所以导致重复运算过多在PTA上有一个运行超时,这个时候才意识到备忘录方法的重要性。在这道题做完之后,又参考了网上的填表方法,同样是O(n²)的时间复杂度用两个for语句从下往上的找到最大值,也是动态规划里的方法之一。
标签:for info 实践 最大 for语句 分析 复杂度 运算 算法
原文地址:https://www.cnblogs.com/zttt/p/11707153.html