标签:str inf www class 计算 十六进制 bsp 超过 href
计算机采用二进制主要是为了方便硬件的实现,电流的通、断,或电压的高、低正好能够表示二进制的0和1两个数码。二进制好处分述如下:
一、可行性:若使用十进制数,则需要这样的电子器件,它必须有能表示0—9数码的10个物理状态,这在技术上是相当困难的(目前为止没有完全解决),而使用二进制数,只需0,1两个状态,技术上轻而易举,如开关的通与断,晶体管中导通与截止等,磁介质的带磁与不带磁。
二、可靠性:二进制只有两种状态,数字传输处理不易出错。
三、简易性:二进制运算法则比较简单,数值、图形、文字等各种形式的信息,需要计算机加工处理时,首先必须按一定的法则转换成二进制数.
用二进制数表示一个数值时,位数比较长,不便书写和记忆,所以人们常用八进制数或十六进制数和十进制数来表示二进制数.
二进制
范围:0、1
性质:逢二进一
八进制
范围:0、1、2、3、4、5、6、7
性质:逢八进一
十进制
范围:0、1、2、3、4、5、6、7、8、9
性质:逢十进一
十六进制
范围:0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F
性质:逢十六进一
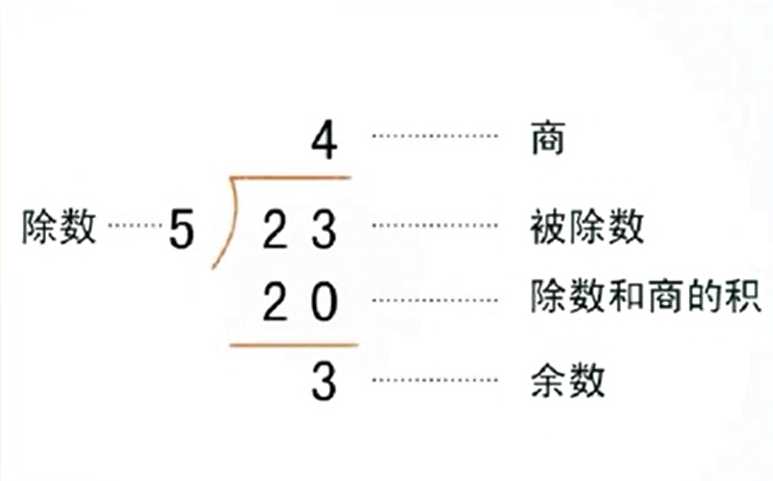
首先我们来看一个除法公式,从这个除法我们可以得出余数的求法。
余数 = 被除数 - (商 * 除数)
3 = 23 - (4 * 5)
高进制转低进制采用辗转相除法
低进制转高进制采用权相加法
十进制数和十六进制数采用8421码翻译成二进制数(适用于15以内的数,如果超过15就需要拆分成15以内的数之和再进行二进制运算)
十进制转换成2进制
100(10)转换成二进制:100 / 2 = 50....余0、50 / 2 = 25....余0、25 / 2 = 12....余1、12 / 2 = 6....余0、6 / 2 = 3....余0、3 / 2 = 1....余1、1 / 2 = 0....余1。
十进制转换成二进制:采用的是辗转相除法,十进制数除以2其得到的商继续除以2直到商为0为止,然后再将得到的余数倒叙排列就是二进制对应的十进制数。比如十进制数100转换成二进制数为1100100。
那么逢二进一又是什么意思?又怎么具体使用呢?
比如十进制数9用二进制数表示:二进制数运算规则是逢二进一,二进制数表示只有数字0和1。
将十进制数9拆分为(1+1) +(1+1) +(1+1) +(1+1) +1 = 10 + 10 + 10 + 10 + 1
其中的(1+1)= 10 就是采用二进制的逢二进一运算规则。
后面的10 + 10 + 10 + 10 + 1 = 10 + 10 + 10 + 10 + 01涉及到二进制的加法,二进制的加法规则很简单,低位和低位相加,高位和高位相加,配合二进制的逢二进一运算规则可以得出最后的答案:(10 + 10) + (10 + 10) + 01 = 100 + 100 + 01 = 1000 + 01 = 1001。
确实上面的十进制数和十六进制数可以采用8421规则得出相应的二进制数,8421码对应着4位二进制数,8对应千位、4对应百位、2对应十位、1对应个位,比如上面的十进制数9按照8421码规则可以很轻松写出其二进制数1001,再比如十六进制数F变化成二进制就是四个1,F(16) = 1111(2)。
高进制转低进制请参照十进制转二进制的方法。
二进制转十进制
口诀:整数二进制用数值乘以2的幂次依次相加,小数二进制用数值乘以2的负幂次然后依次相加。
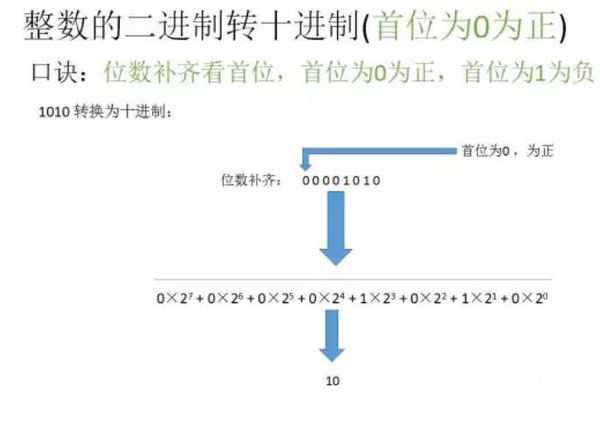
1、整数二进制转换为十进制:首先将二进制数补齐位数,首位如果是0就代表是正整数,如果首位是1则代表是负整数。
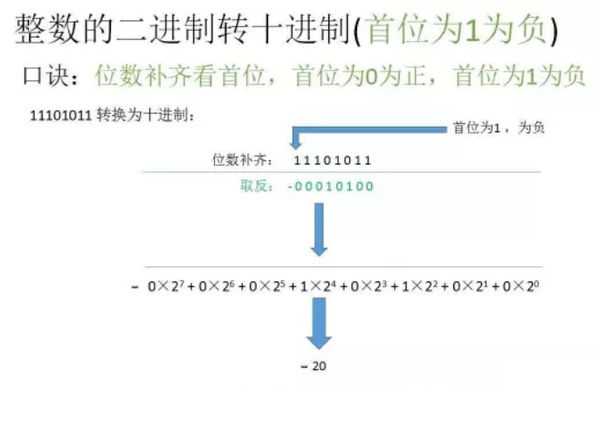
若二进制补足位数后首位为1时,如下图所示,就需要先取反再换算:
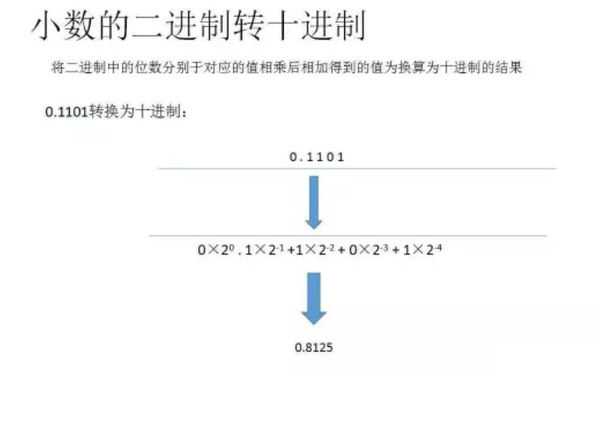
2、小数的二进制转换为十进制:将二进制中的四位小数分别于下边(如下图所示)对应的值相乘后相加得到的值即为换算后的十进制。
标签:str inf www class 计算 十六进制 bsp 超过 href
原文地址:https://www.cnblogs.com/iBoundary/p/11710467.html