标签:style blog http io color os ar for sp
给定训练集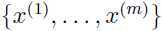 ,想把这些样本分成不同的子集,即聚类,
,想把这些样本分成不同的子集,即聚类,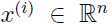 ,但是这是个无标签数据集,也就是说我们再聚类的时候不能利用标签信息,所以这是一个无监督学习问题。
,但是这是个无标签数据集,也就是说我们再聚类的时候不能利用标签信息,所以这是一个无监督学习问题。
k-means聚类算法的流程如下:
1. 随机初始化聚类中心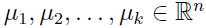
2. a. 对与每一个聚类中心,计算所有样本到该聚类中心的距离,然后选出距离该聚类中心最近的几个样本作为一类;
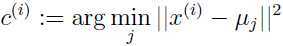
这个公式的意思是,某个样本 i 属于哪一类,取决于该样本距离哪一个聚类中心最近,步骤a就是利用这个规则实现。
b. 对上面分成的k类,根据类里面的样本,重新估计该类的中心:
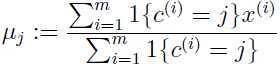
对于新的聚类中心,重复a,这里1{...}是一个真值判断,例如1{3=2}=0,1{3=3}=1.
c. 重复a和b直至收敛
但是k-means真的能保证收敛吗?k-means的目的是选出聚类中心和每一类的样本,定义失真函数:
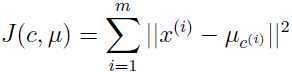
这个函数衡量的是某个聚类的中心与该类中所有样本距离的平方和,根据上面k-means的算法,可以看出,a 是固定聚类中心,选择该类的样本,b 是样本固定,调整聚类中心,即每次都是固定一个变量,调整另一个变量,所以k-means完全是在针对失真函数 J 坐标上升,这样,J 必然是单调递减,所以J的值必然收敛。在理论上,这种方法可能会使得k-means在一些聚类结果之间产生震荡,即几组不同的 c 和 μ 有着相同的失真函数值,但是这种情况在实际情况中很少出现。
由于失真函数是一个非凸函数,所以坐标上升不能保证该函数全局收敛,即失真函数容易陷入局部收敛。但是大多数情况下,k-means都可以产生不错的结果,如果担心陷入局部收敛,可以多运行几次k-means(采用不同的随机初始聚类中心),然后从多次结果中选出失真函数最小的聚类结果。
下面是一个简单k-means的C++代码,对{1, 2, 3, 11, 12, 13, 21, 22, 23}这9个样本值聚类:
1 #include<iostream> 2 #include<cmath> 3 #include<vector> 4 #include<ctime> 5 using namespace std; 6 typedef unsigned int uint; 7 8 struct Cluster 9 { 10 vector<double> centroid; 11 vector<uint> samples; 12 }; 13 double cal_distance(vector<double> a, vector<double> b) 14 { 15 uint da = a.size(); 16 uint db = b.size(); 17 if (da != db) cerr << "Dimensions of two vectors must be same!!\n"; 18 double val = 0.0; 19 for (uint i = 0; i < da; i++) 20 { 21 val += pow((a[i] - b[i]), 2); 22 } 23 return pow(val, 0.5); 24 } 25 vector<Cluster> k_means(vector<vector<double> > trainX, uint k, uint maxepoches) 26 { 27 const uint row_num = trainX.size(); 28 const uint col_num = trainX[0].size(); 29 30 /*初始化聚类中心*/ 31 vector<Cluster> clusters(k); 32 uint seed = (uint)time(NULL); 33 for (uint i = 0; i < k; i++) 34 { 35 srand(seed); 36 int c = rand() % row_num; 37 clusters[i].centroid = trainX[c]; 38 seed = rand(); 39 } 40 41 /*多次迭代直至收敛,本次试验迭代100次*/ 42 for (uint it = 0; it < maxepoches; it++) 43 { 44 /*每一次重新计算样本点所属类别之前,清空原来样本点信息*/ 45 for (uint i = 0; i < k; i++) 46 { 47 clusters[i].samples.clear(); 48 } 49 /*求出每个样本点距应该属于哪一个聚类*/ 50 for (uint j = 0; j < row_num; j++) 51 { 52 /*都初始化属于第0个聚类*/ 53 uint c = 0; 54 double min_distance = cal_distance(trainX[j],clusters[c].centroid); 55 for (uint i = 1; i < k; i++) 56 { 57 double distance = cal_distance(trainX[j], clusters[i].centroid); 58 if (distance < min_distance) 59 { 60 min_distance = distance; 61 c = i; 62 } 63 } 64 clusters[c].samples.push_back(j); 65 } 66 67 /*更新聚类中心*/ 68 for (uint i = 0; i < k; i++) 69 { 70 vector<double> val(col_num, 0.0); 71 for (uint j = 0; j < clusters[i].samples.size(); j++) 72 { 73 uint sample = clusters[i].samples[j]; 74 for (uint d = 0; d < col_num; d++) 75 { 76 val[d] += trainX[sample][d]; 77 if (j == clusters[i].samples.size() - 1) 78 clusters[i].centroid[d] = val[d] / clusters[i].samples.size(); 79 } 80 } 81 } 82 } 83 return clusters; 84 } 85 86 int main() 87 { 88 vector<vector<double> > trainX(9,vector<double>(1,0)); 89 //对9个数据{1 2 3 11 12 13 21 22 23}聚类 90 double data = 1.0; 91 for (uint i = 0; i < 9; i++) 92 { 93 trainX[i][0] = data; 94 if ((i+1) % 3 == 0) data += 8; 95 else data++; 96 } 97 98 /*k-means聚类*/ 99 vector<Cluster> clusters_out = k_means(trainX, 3, 100); 100 101 /*输出分类结果*/ 102 for (uint i = 0; i < clusters_out.size(); i++) 103 { 104 cout << "Cluster " << i << " :" << endl; 105 106 /*子类中心*/ 107 cout << "\t" << "Centroid: " << "\n\t\t[ "; 108 for (uint j = 0; j < clusters_out[i].centroid.size(); j++) 109 { 110 cout << clusters_out[i].centroid[j] << " "; 111 } 112 cout << "]" << endl; 113 114 /*子类样本点*/ 115 cout << "\t" << "Samples:\n"; 116 for (uint k = 0; k < clusters_out[i].samples.size(); k++) 117 { 118 uint c = clusters_out[i].samples[k]; 119 cout << "\t\t[ "; 120 for (uint m = 0; m < trainX[0].size(); m++) 121 { 122 cout << trainX[c][m] << " "; 123 } 124 cout << "]\n"; 125 } 126 } 127 return 0; 128 }
下面是4次运行结果:
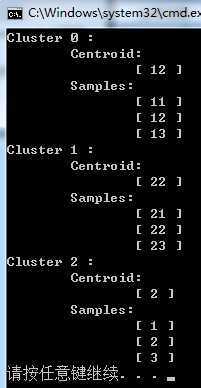
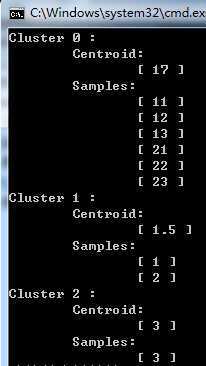
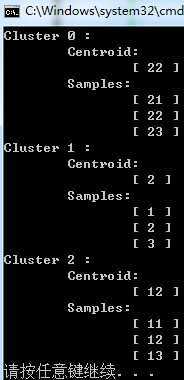
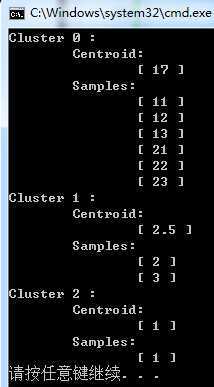
由于数据简单,容易看出第一次和第是三次结果是理想的,而第二次和第四次都是较差出的聚类结果,即上面说的失真函数陷入了局部最优,所以在实践中多次运行,取出较好的聚类结果。
标签:style blog http io color os ar for sp
原文地址:http://www.cnblogs.com/90zeng/p/k_means.html