标签:bsp 经验 rgs python imp shape 统计 代码 自己的
对于该图来说,x轴对应的是肿瘤的大小,y轴对应的是时间,蓝色样本表示恶性肿瘤,红色样本表示良性肿瘤,我们先假设k=3,这个k先不考虑怎么得到,先假设这个k是通过程序员经验得到。
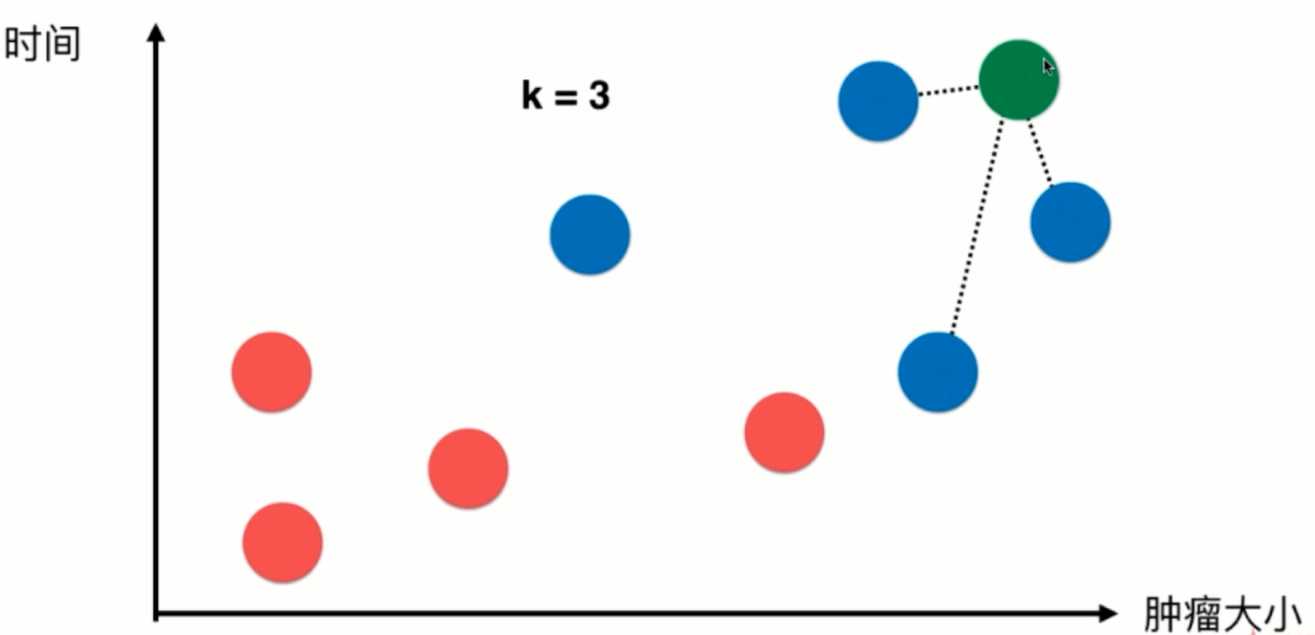
此时来了一个新样本,我们选取离该样本最近的三个样本点,根据他们自身的结果进行投票,如图得到蓝色:红色=1:2,那么我们可以预测该绿色样本可能也是良性肿瘤。
1 #首先导入代码需要的package
2 import numpy as np
3 import matplotlib
4 import matplotlib.pyplot as plt
5 #此处先使用我们模拟的数据进行算法的入门模拟
6 #特征点的集合
7 raw_data_X = [[3.393533211, 2.331273381],
8 [3.110073483, 1.781539638],
9 [1.343808831, 3.368360954],
10 [3.582294042, 4.679179110],
11 [2.280362439, 2.866990263],
12 [7.423436942, 4.696522875],
13 [5.745051997, 3.533989803],
14 [9.172168622, 2.511101045],
15 [7.792783481, 3.424088941],
16 [7.939820817, 0.791637231]
17 ]
18 #0就代表良性肿瘤,1就代表恶性肿瘤
19 raw_data_y = [0, 0, 0, 0, 0, 1, 1, 1, 1, 1]
20 #我们使用raw_data_X和raw_data_y作为我们的训练集
21 X_train = np.array(raw_data_X)
22 Y_train = np.array(raw_data_y)
23 #此时可以查看两个训练集数据输出显示
24 In[1]: X_train
25 ‘‘‘
26 Out [1]:array([[3.39353321, 2.33127338],
27 [3.11007348, 1.78153964],
28 [1.34380883, 3.36836095],
29 [3.58229404, 4.67917911],
30 [2.28036244, 2.86699026],
31 [7.42343694, 4.69652288],
32 [5.745052 , 3.5339898 ],
33 [9.17216862, 2.51110105],
34 [7.79278348, 3.42408894],
35 [7.93982082, 0.79163723]])
36 ‘‘‘
37 In[2]: Y_train
38 ‘‘‘
39 Out[2]:array([0, 0, 0, 0, 0, 1, 1, 1, 1, 1])
40 ‘‘‘
41 #我们可以尝试绘制原训练集的散点图
42 plt.scatter(X_train[Y_train == 0, 0],X_train[Y_train == 0,1], color = "red")
43 plt.scatter(X_train[Y_train == 1, 0],X_train[Y_train == 1,1], color = "blue")
44 plt.show() #显示该散点图
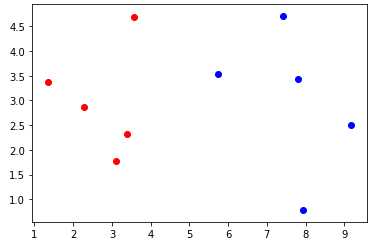
训练集绘制的散点图如上图所示,红色的散点表示为良性肿瘤的样本,蓝色表示为恶性肿瘤的样本
1 #此时,来了一个新样本数据 x
2 x = np.array([8.093607318,3.365731514])
3 #将新来的样本点绘入图像中,先绘制原训练集散点图像,再使用绿色表示新样本点进行绘制
4 plt.plot(X_train[Y_train == 0, 0],X_train[Y_train == 0, 1], color = "red")
5 plt.plot(X_train[Y_train == 1, 0],X_train[Y_train == 1, 1], color = "blue")
6 plt.plot(x[0],x[1], color = "green")
7 plt.show()
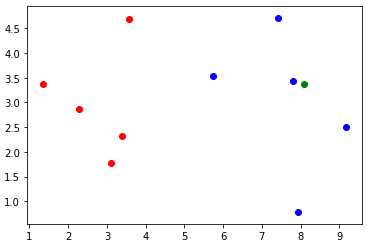
带新样本点绘制的散点图如上图所示
1 #此时我们假设根据程序员经验选取 k = 6
2 k = 6
3 #然后我们需要进行在原训练集中选取k个离新样本点最近的6个样本点
4 #两点之间的距离使用欧拉公式进行计算,

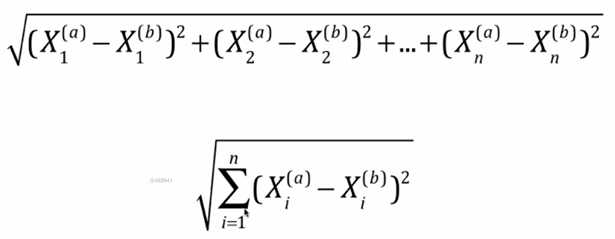
1 #所以根据上图公式我们可以进行计算所有训练集的样本点与新的绿色样本点的距离
2 #此处需要使用到开平方根,所以导入相应package
3 from math import sqrt
4 #使用distances进行存储所有距离值
5 distances = []
6 # 因为所有的训练集的X Y 信息都存储在X_train中,所以我们使用for循环进行遍历所有的样本点信息进行计算
7 for x_train in X_train:
8 #使用d暂存距离
9 d = sqrt(np.sum((x_train - x) ** 2))
10 #使用append将距离d存到distances
11 distances.append(d)
12 #上面for循环部分也能够使用列表推导式进行简化代码
13 distances = [sqrt(np.sum((X_train - x) ** 2)) for x_train in X_train]
14 #此时我们能够输出distances的值进行查看一下
15 In[3]: distances
16 Out[3]: [4.812566907609877,
17 5.229270827235305,
18 6.749798999160064,
19 4.6986266144110695,
20 5.83460014556857,
21 1.4900114024329525,
22 2.354574897431513,
23 1.3761132675144652,
24 0.3064319992975,
25 2.5786840957478887]
26 #此时我们的distances里面存储所有的训练样本点与新样本点的距离
27 #因为我们需要找到距离新样本点最近的k(此处k=6)个样本点,所有我们需要对distances进行排序
28 #此处我们使用np.argsort对其进行值的索引的排序,就不会对其值逻辑位置进行影响,使用nearest存储排序后的结果
29 nearest = np.argsort(distances)
30 #找到前6个索引对应的值对应的Y_train的值
31 topk_y = [Y_train[i] for i in nearest[:k]]
32 #此时我们输出topk_y的值
33 In[4]: topk_y
34 Out[4]:[1, 1, 1, 1, 1, 0]
35 #我们能够看到此时对应的topk_y中存储着离新样本点最近的k个训练样本点的结果(0/1 良性肿瘤/恶性肿瘤)
36 #然后我们对结果进行“投票”操作,票数最多的结果作为新样本的预测结果(前面已经介绍)
37 #可以调用Collections包中的Counter方法对topk_y进行唱票统计
38 from Collections import Counter
39 votes = Counter(topk_y)
40 #此时我们能够输出votes的值进行查看
41 In[4]: votes
42 Out[4]: Counter({1: 5, 0: 1})
43 #我们能够使用most_common(vaule)方法进行取最大票数的前value位
44 In[5]: votes.most_common(1)
45 Out[5]: [(1, 5)]
46 #查看该输出我们能够得到
47 predict_y = votes.most_common(1)[0][0]
48 In[6]: predict_y
49 Out[6]: 1
50 #此时kNN算法结束,根据所得到的预测结果,我们能够预测该新的样本可能是恶性肿瘤
1 import numpy as np
2 from math import sqrt
3 from collections import Counter
4
5 def kNN_classify(k, X_train, Y_train, x):
6 assert 1<= k <= X_train.shape[0],"k must be valid"
7 assert X_train.shape[0] == Y_train.shape[0], 8 "the size of X-train must equal to the size of Y_train"
9 assert X_train.shape[1] == x.shape[0].10 "the feature number of x must be equal to X_train"
11
12 distances = [sqrt(np.sum((X_train - x) ** 2)) for x_train in X_train]
13 nearest = np.argsort(distances)
14
15 topk_y = [Y_train[i] for i in nearest[:k]]
16 votes = Counter(topk_y)
17
18 return votes.most_common(1)[0][0]
最基础的分类算法-k近邻算法 kNN简介及Jupyter基础实现及Python实现
标签:bsp 经验 rgs python imp shape 统计 代码 自己的
原文地址:https://www.cnblogs.com/Liuyt-61/p/11738399.html