标签:als put 邻接 起点 strong 数据结构 details ret 使用
现在你总共有 n 门课需要选,记为?0?到?n-1。
在选修某些课程之前需要一些先修课程。?例如,想要学习课程 0 ,你需要先完成课程 1 ,我们用一个匹配来表示他们: [0,1]
给定课程总量以及它们的先决条件,判断是否可能完成所有课程的学习?
示例 1:
输入: 2, [[1,0]]
输出: true
解释:?总共有 2 门课程。学习课程 1 之前,你需要完成课程 0。所以这是可能的。
示例 2:
输入: 2, [[1,0],[0,1]]
输出: false
解释:?总共有 2 门课程。学习课程 1 之前,你需要先完成?课程 0;并且学习课程 0 之前,你还应先完成课程 1。这是不可能的。
说明:
输入的先决条件是由边缘列表表示的图形,而不是邻接矩阵。详情请参见图的表示法。
你可以假定输入的先决条件中没有重复的边。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/course-schedule
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
1.邻接矩阵:矩阵m[i][j]表示i到j是否有弧/权重。有稀疏问题。
2.临接表:对图的每个节点,用一个单向链表列出从该节点出发的所有弧,链表中每个节点对应于一条出弧。
3.关联矩阵:矩阵每一行是一个点,每一列是描述一个弧(1表示弧的起点,-1表示弧的终点)。有稀疏问题。
4.弧表示法
5.星型表示法
很好的参考文章:https://blog.csdn.net/woaidapaopao/article/details/51732947
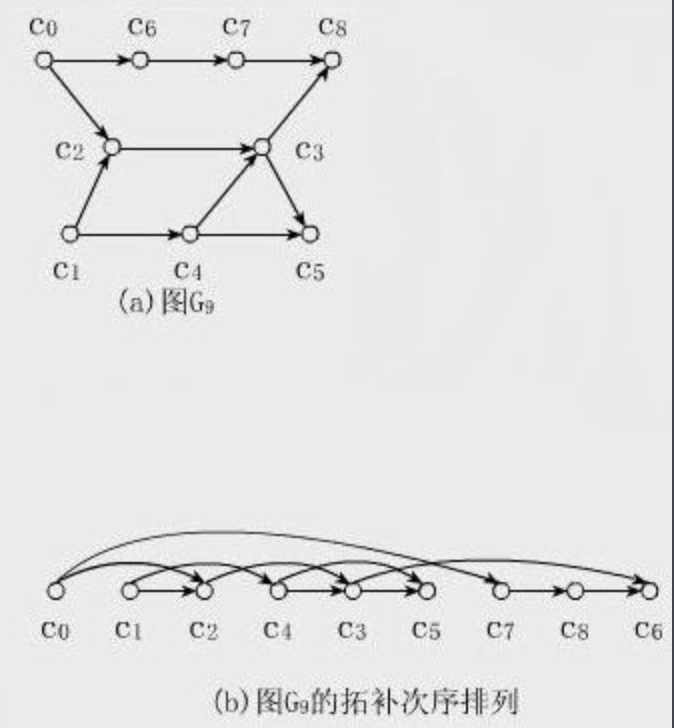
拓扑排序的另一个重要作用是可以判断有向图是否无环
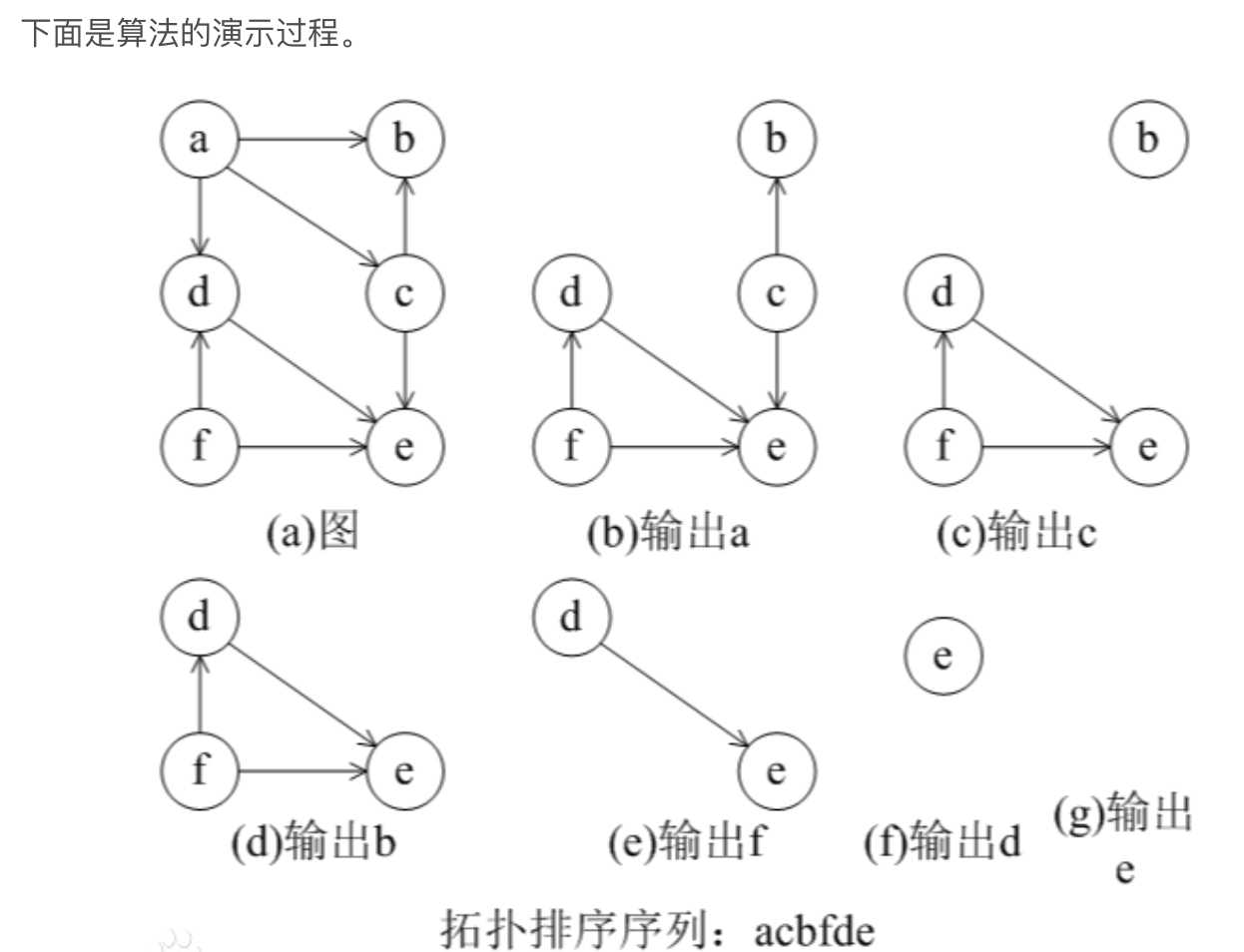
当还有入度为0的点未放入结果序列:
2 从网中删除此顶点及所有出边。
结束后,若结果集中未包含全部点(即产生入度不为0的点无法放入),则说明图中有环,否则结果序列就是一个拓扑序列。
public boolean canFinish(int numCourses, int[][] prerequisites) {
int pointCnt = numCourses;// 未放入拓扑序列的点的个数
HashMap<Integer, List<Integer>> adjList = new HashMap<>();// 邻接表
int[] inDegree = new int[numCourses];// 存放顶点入度
LinkedList<Integer> pointQue = new LinkedList<>();// 存放当前待处理的入度为0的顶点
for (int[] edge : prerequisites) {
// 初始化邻接表
List<Integer> tempList = adjList.getOrDefault(edge[0], new LinkedList<>());
tempList.add(edge[1]);
adjList.put(edge[0], tempList);
// 初始化顶点入度数组
inDegree[edge[1]]++;
}
// 入度为0的点放入队列
for (int i = 0; i < numCourses; ++i) {
if (inDegree[i] == 0) {
pointQue.addLast(i);
}
}
// 删掉入度为0的点,删掉关联的所有边;更新pointCnt;更新入度数组,将新的入度为0的点入队。
while (!pointQue.isEmpty()) {
int u = pointQue.removeFirst();
pointCnt--;
if (adjList.containsKey(u)) {//
for (int v : adjList.get(u)) {
inDegree[v]--;
if (inDegree[v] == 0) {
pointQue.push(v);
}
}
}
}
return pointCnt == 0;
}https://blog.csdn.net/qq_41713256/article/details/80805338
标签:als put 邻接 起点 strong 数据结构 details ret 使用
原文地址:https://www.cnblogs.com/coding-gaga/p/11745782.html