史上最全最小生成树算法

标签：push   bit   mes   memset   ret   its   img   check   gif   

我不信还有人比这个全

总共三种，大家最熟悉的\(Kruskal\)，\(Prim\)以及不那么熟悉的\(Bor?vka\)。

时间复杂度：\(Kruskal:\mathcal{O}(MlogM),Prim:\mathcal{O}(N^2),Bor?vka:\mathcal{O}(MlogN)\)

堆优化\(Prim\)可以到\(\mathcal{O}(NlogN)\)。

实现过程：

\(Kruskal:\)对所有边排序，从小到大加入，如果会成环就不加入。

\(Prim:\)任选一个点加入最小生成树点集\(V\)中，找到最小的一条边\(E\)，其一端在\(V\)中，一端不在，将这样的边加入最小生成树中，重复上述操作即可。

\(Bor?vka\)：开始每个点自成一个联通块。 每次对所有联通块找一条边权最小的边（如果有边权相同，就按编号取最小的编号），其中一端在该联通块内而另一端不在，接下来加入这些边并合并联通块。 重复上述操作直到没有联通块可以合并。

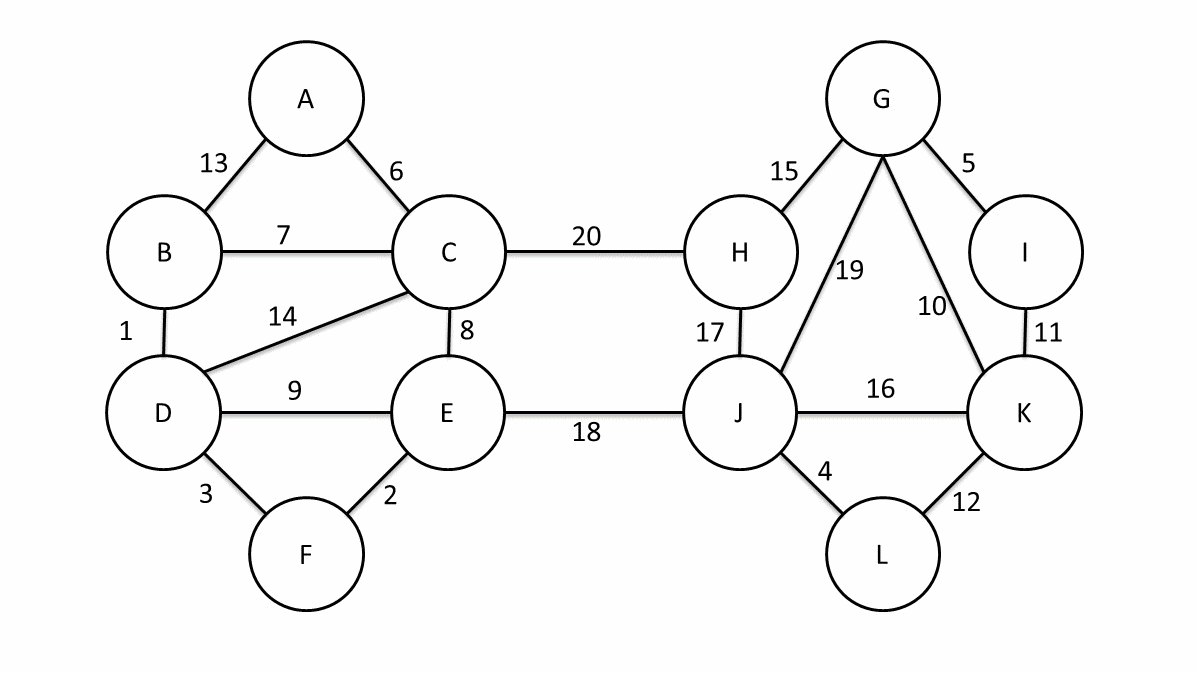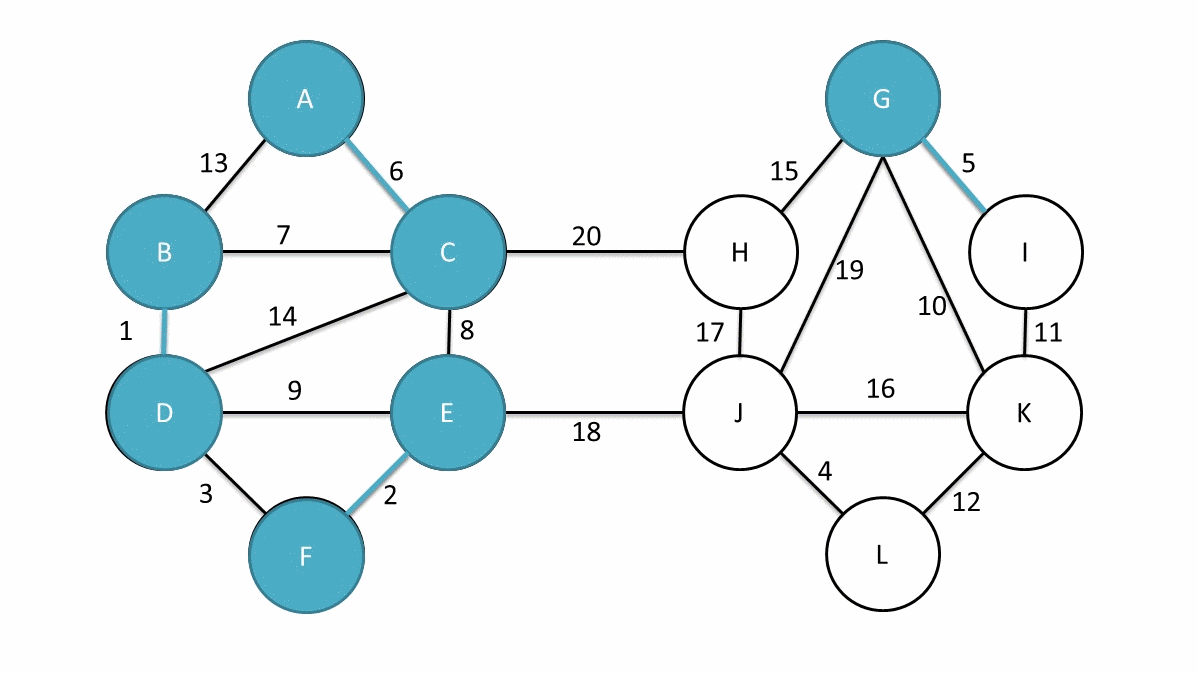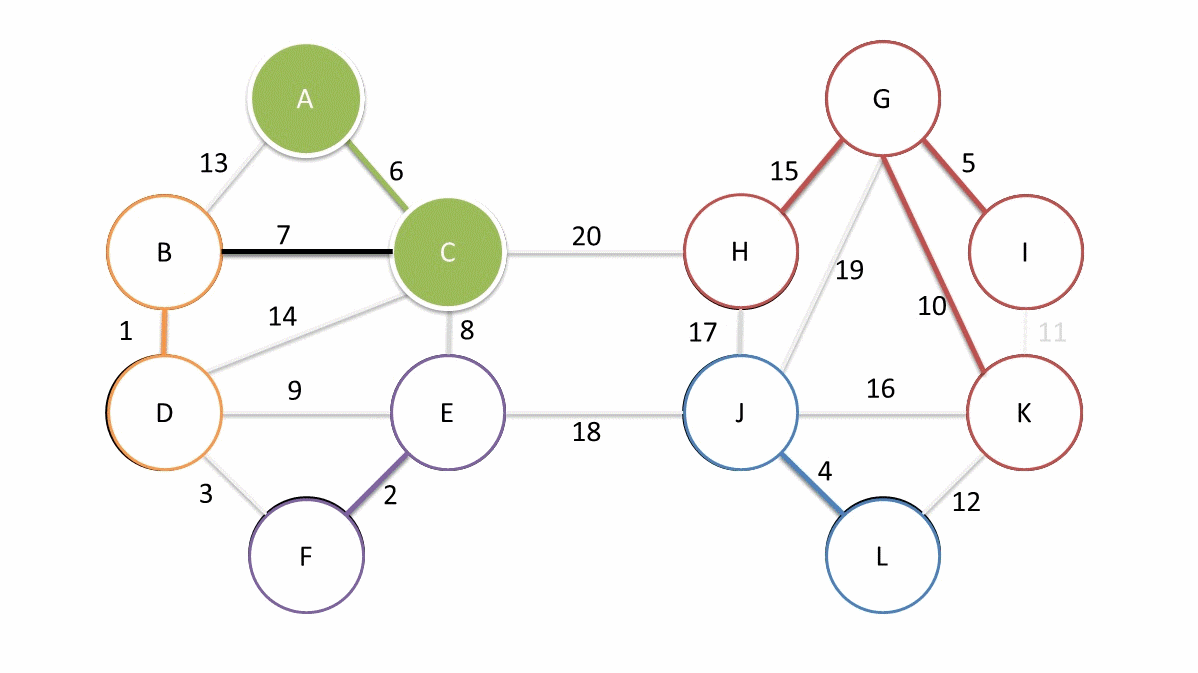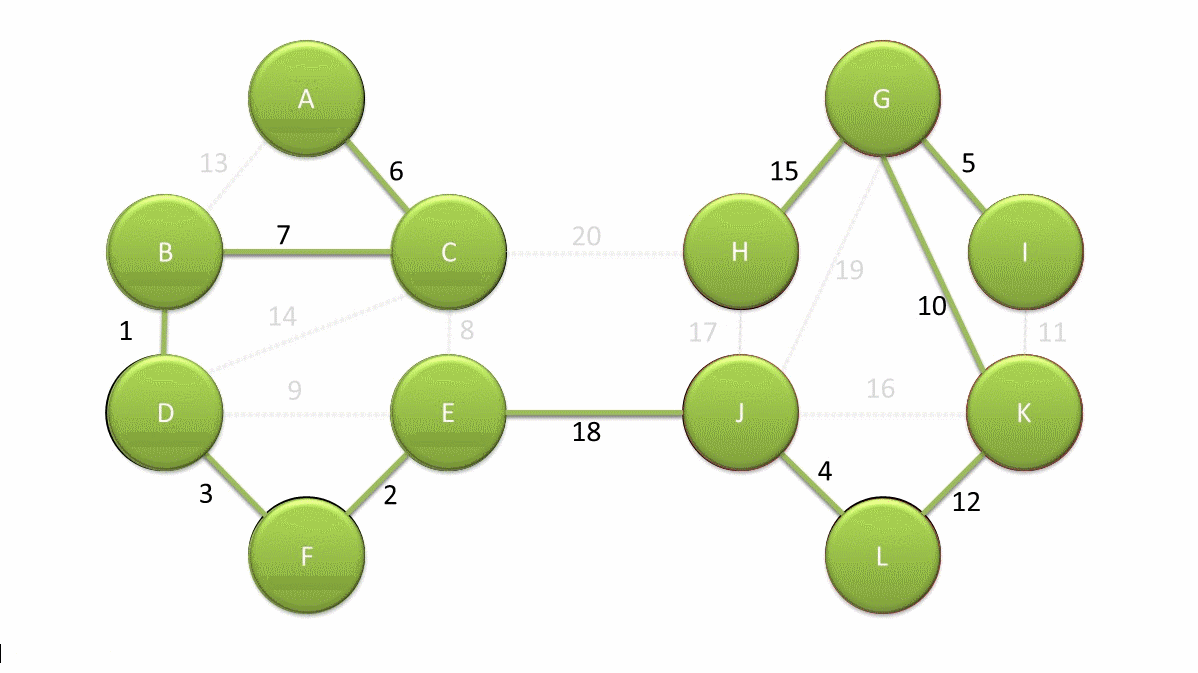
这是\(Bor?vka\)的动态演示，可以说是很清晰了。这个算法就像是\(Prim\)的进阶版本对吧。。。

它的\(log\)是哪来的呢？实际上，它每次加边合并之后联通块数会减少一半，所以总共只要进行\(log\)次。

上一个总的代码（堆优化\(Prim\)用的是\(Dijstra\)写法）

#include<bits/stdc++.h>
using namespace std;
inline int read()
{
    int f=1,w=0;char x=0;
    while(x<'0'||x>'9') {if(x=='-') f=-1; x=getchar();}
    while(x!=EOF&&x>='0'&&x<='9') {w=(w<<3)+(w<<1)+(x^48);x=getchar();}
    return w*f;
}
const int N=5e3+10;
const int M=2e5+10;
int n,m,ans;
int Cnt,num_edge;
int head[M],fa[N];
int Vis[M],Dis[N],Min[M];
struct Line{int u,v,dis;} Lin[M];
struct Edge{int next,to,dis;} edge[M<<1];
inline int Find(int x) {return fa[x]==x?x:fa[x]=Find(fa[x]);}
inline bool Cmp(Line x,Line y) {return x.dis<y.dis;}
inline void Add(int from,int to,int dis)
{
    edge[++num_edge].next=head[from];
    edge[num_edge].dis=dis;
    edge[num_edge].to=to;
    head[from]=num_edge;
}
inline void Kruskal()
{
    sort(Lin+1,Lin+m+1,Cmp);
    for(int i=1;i<=n;i++) fa[i]=i;
    for(int i=1;i<=m;i++)
    {
        int u=Find(Lin[i].u),v=Find(Lin[i].v);
        if(u!=v) fa[u]=v,ans+=Lin[i].dis;
    }
    printf("%d",ans);
}
inline void Simple_Prim(int Now)
{
    memset(Dis,0x3f,sizeof(Dis));Dis[Now]=0;
    for(int i=head[Now];i;i=edge[i].next)
        Dis[edge[i].to]=min(Dis[edge[i].to],edge[i].dis);
    while(++Cnt<n)
    {
        int Min=Dis[0];Vis[Now]=1;
        for(int i=1;i<=n;i++)
            if(!Vis[i]&&Min>Dis[i]) Now=i,Min=Dis[i];
        ans+=Min;
        for(int i=head[Now];i;i=edge[i].next)
            if(Dis[edge[i].to]>edge[i].dis&&!Vis[edge[i].to])
                Dis[edge[i].to]=edge[i].dis;
    }
    printf("%d",ans);
}
priority_queue<pair<int,int> > Q;
inline void Priority_Prim(int Now)
{
    memset(Dis,0x3f,sizeof(Dis));
    Dis[1]=0;Q.push(make_pair(0,1));
    while(Q.size()&&Cnt<n)
    {
        int x=Q.top().second,dis=-Q.top().first;Q.pop();
        if(Vis[x]) continue;++Cnt,ans+=dis,Vis[x]=1;
        for(int i=head[x];i;i=edge[i].next)
            if(Dis[edge[i].to]>edge[i].dis)
                Dis[edge[i].to]=edge[i].dis,Q.push(make_pair(-edge[i].dis,edge[i].to));
    }
    printf("%d",ans);
}
inline bool Check(int x,int y)
{
    if(!y) return 1;
    return Lin[x].dis!=Lin[y].dis?Lin[x].dis<Lin[y].dis:x<y;
}
inline void Boruvka()
{
    int Jud=1;
    for(int i=1;i<=n;i++) fa[i]=i;
    while(Jud)
    {
        Jud=0;memset(Min,0,sizeof(Min));
        for(int i=1;i<=m;i++)
            if(!Vis[i]&&Find(Lin[i].u)!=Find(Lin[i].v))
            {
                int u=Find(Lin[i].u),v=Find(Lin[i].v);
                if(Check(i,Min[u])) Min[u]=i;
                if(Check(i,Min[v])) Min[v]=i;
            }
        for(int i=1;i<=n;i++)
            if(Min[i]&&!Vis[Min[i]])
            {
                Jud=1;ans+=Lin[Min[i]].dis;Vis[Min[i]]=1;
                fa[Find(Lin[Min[i]].u)]=Find(Lin[Min[i]].v);
            }
    }
    printf("%d",ans);
}
int main(){
#ifndef ONLINE_JUDGE
    freopen("A.in","r",stdin);
#endif
    n=read(),m=read();
    for(int i=1;i<=m;i++)
        Lin[i].u=read(),Lin[i].v=read(),Lin[i].dis=read();
    for(int i=1;i<=m;i++)
        Add(Lin[i].u,Lin[i].v,Lin[i].dis),Add(Lin[i].v,Lin[i].u,Lin[i].dis);
    //Kruskal();
    //Simple_Prim(1);
    //Priority_Prim(1);
    //Boruvka();
}

史上最全最小生成树算法

标签：push   bit   mes   memset   ret   its   img   check   gif   

原文地址：https://www.cnblogs.com/wo-shi-zhen-de-cai/p/11755202.html