标签:-o std shadow char else print printf roc 依次
这些是较为简单的二叉树的建立、遍历、销毁的递归算法。
假设二叉树都用二叉链作为存储结构,并约定根节点的指针用T表示。
为了简化问题,我们用char类型的字符代替树中的数据,并且用前序遍历的算法,建立二叉树过程如下:
测试的源代码如下:
1 #include<stdio.h> 2 #include<stdlib.h> 3 4 typedef struct BTREE { 5 char data; 6 struct BTREE *lchild, *rchild; 7 }BT,*LBTREE; 8 9 10 11 void Creat(LBTREE *T) //前序遍历的递归算法 12 { 13 char ch; 14 ch=getchar(); //从缓冲一个个读取字符 15 if (ch == ‘ ‘) //输入空格则该节点为空(即不存在) 16 *T = NULL; 17 else 18 { 19 (*T) = (LBTREE)malloc(sizeof(BT)); 20 (*T)->data=ch; 21 Creat(&((*T)->lchild)); 22 Creat(&((*T)->rchild)); 23 } 24 25 } 26 27 void Pretravers(LBTREE T) //前序遍历 28 { 29 if (T != NULL) 30 { 31 printf("% c", T->data); 32 Pretravers(T->lchild); 33 Pretravers(T->rchild); 34 } 35 36 } 37 38 void Inortravers(LBTREE T) //中序遍历 39 { 40 if (T != NULL) 41 { 42 Inortravers(T->lchild); 43 printf("% c", T->data); 44 Inortravers(T->rchild); 45 } 46 } 47 48 void Postravers(LBTREE T) //后续遍历 49 { 50 if (T != NULL) 51 { 52 Postravers(T->lchild); 53 Postravers (T->rchild); 54 printf("% c", T->data); 55 } 56 } 57 58 void Distroyb(LBTREE T) //销毁二叉树(同样使用递归的方式) 59 { 60 if (T != NULL) 61 { 62 Distroyb(T->lchild); 63 Distroyb(T->rchild); 64 free(T); 65 } 66 } 67 68 void main(void) 69 { 70 LBTREE T=NULL; 71 puts("输入二叉树数据"); //这里用的是 72 getchar(), //会读取换行符,应将所有数据在一行输入 73 Creat(&T); 74 puts("前序遍历输出:"); 75 Pretravers(T); 76 puts(""); 77 puts("中序遍历输出:"); 78 Inortravers(T); 79 puts(""); 80 puts("后续遍历输出:"); 81 Postravers(T); 82 puts(""); 83 Distroyb(T); 84 }
结果如下: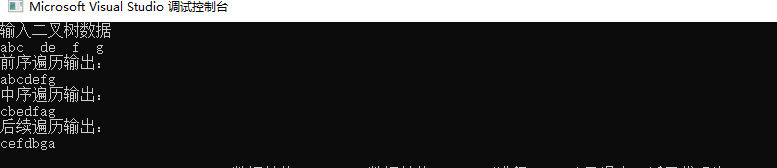
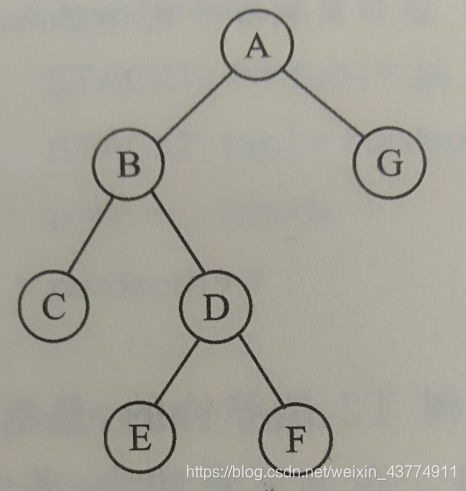
建立的二叉树是这样的:
标签:-o std shadow char else print printf roc 依次
原文地址:https://www.cnblogs.com/codeloop/p/11775758.html