[总结]RMQ问题&ST算法

标签：http   ++   inline   lis   code   bit   href   maximum   neu   

一、ST算法

ST算法(Sparse Table Algorithm)是用于解决RMQ问题(区间最值问题，即Range Maximum/Minimum Question)的一种著名算法。
ST算法能在复杂度为\(O(NlogN)\)的预处理后，以\(O(1)\)的复杂度在线处理序列区间内的最大值/最小值。
值得注意的是，ST算法并不能处理需要修改点权的区间最值问题。

• ST表的实现同样依据倍增思想，设\(f(i,j)\)表示序列下标区间为\([i,i+2^{j}-1]\)的最值，即从\(i\)在内的\(2^j\)个数的最大值。
  递推过程中的转移方程与LCA的思想类似，新的区间最值由原区间翻倍推出，转移方程为：
  \[f[i,j]=max(f[i,j-1],f[i+2^{j-1},j-1])\]
  \[f[i,j]=min(f[i,j-1],f[i+2^{j-1},j-1])\]
  图示(很良心)：
  

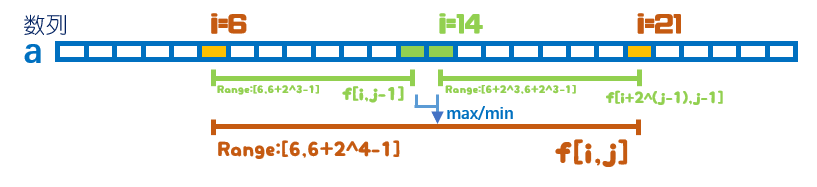
• 当我们询问任意区间[l,r]的最大/最小值的时候，我们计算出一个\(k\)，使得\(2^k \lt r-l+1\leq 2^{k+1}\)，这样保证我们的覆盖长度\(2^k\)是区间能覆盖最大的长度。此时询问两个区间\([l,r]\)，\([r-2^{k}+1,r]\)的极值就能求出该区间的最大/最小值，尽管区间可能重叠，由于我们求的是最大/最小值，因此重叠区间对答案没有影响。
  图示(查询[3,23]区间最值)：
  

二、ST算法の具体实现

1. 初始化

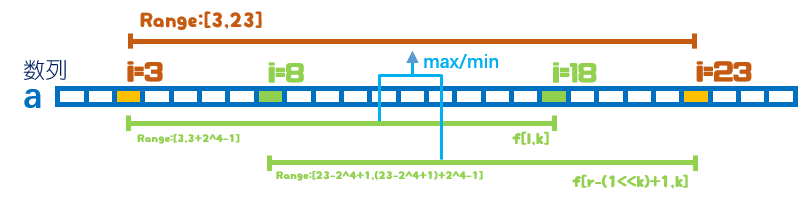
for(int i=1;i<=n;i++){
    scanf("%d",a[i]);
    f[i][0]=a[i];//[i,i]的最值就是a[i]
}

2. 求出ST表

int maxn=log(n)/log(2)+1;
for(int j=1;j<maxn;j++)
    for(int i=1;i<=n-(1<<j)+1;i++)
        f[i][j]=max(f[i][j-1],f[i+(1<<j-1)][j-1]);

3. 询问

询问[l,r]的最大值，ans为答案。

int k=log(r-l+1)/log(2);
int ans=max(f[l][k],f[r-(1<<k)+1][k]);

附：log(n)函数求出的值是\(lgn\)，为了求出\(log_2n\)，我们可以使用换底公式：\(log_2n=\frac{lgn}{lg2}\)解决，时间复杂度为\(O(1)\)。
除此之外，如果有同学认为\(log()\)常数大，我们同样可以手动求出\(log_2n\)的值：

Log[0]=-1;
for(int i=1;i<=n;i++) Log[i]=Log[i>>1]+1;

三、例题

例1：P3865 【模板】ST表

Code：

#include<bits/stdc++.h>
const int logN=25;
const int N=1e7;
using namespace std;
int a[N],f[N][logN];
int m,n,x,y;
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++){
        scanf("%d",&a[i]);
        f[i][0]=a[i];
    } 
    int maxn=log(n)/log(2)+1;
    for(int j=1;j<maxn;j++)
        for(int i=1;i+(1<<j)-1<=n;i++)
            f[i][j]=max(f[i][j-1],f[i+(1<<j-1)][j-1]);
    for(int i=1;i<=m;i++){
        scanf("%d%d",&x,&y);
        int k=log(y-x+1)/log(2);
        printf("%d\n",max(f[x][k],f[y-(1<<k)+1][k]));
    }
    return 0;
}

例2：P2880 [USACO07JAN]平衡的阵容Balanced Lineup

分别预处理出最大值和最小值，询问时相减。
Code：

#include<bits/stdc++.h>
using namespace std;
int n,q,f[50010][25],g[50010][25],a[50010];
int main()
{
    scanf("%d%d",&n,&q);
    for(int i=1;i<=n;i++) scanf("%d",&a[i]),f[i][0]=g[i][0]=a[i];
    int maxn=log(n)/log(2)+1;
    for(int j=1;j<=maxn;j++)
        for(int i=1;i+(1<<j)-1<=n;i++){
            f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]);
            g[i][j]=min(g[i][j-1],g[i+(1<<(j-1))][j-1]);
        }
    for(int i=1,l,r;i<=q;i++){
        scanf("%d%d",&l,&r);
        int k=log(r-l+1)/log(2);
        int ans=max(f[l][k],f[r-(1<<k)+1][k])-min(g[l][k],g[r-(1<<k)+1][k]);
        printf("%d\n",ans); 
    } 
    return 0;
}

[总结]RMQ问题&ST算法

标签：http   ++   inline   lis   code   bit   href   maximum   neu   

原文地址：https://www.cnblogs.com/cyanigence-oi/p/11785494.html