标签:范围 组合 art 技术 缓存 递归算法 ram turn for
归并排序是一个典型的基于分治的递归算法。它不断地将原数组分成大小相等的两个子数组(可能相差1),最终当划分的子数组大小为1时,将划分的有序子数组组合并成一个更大的有序数组。
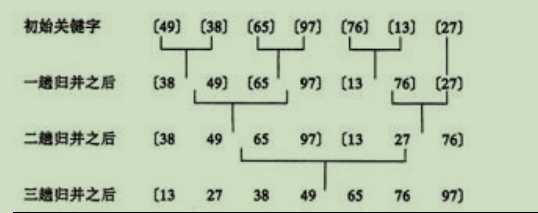
算法分析:
分,也就是把原数组划分成两个子数组的过程。
治,它将两个有序数组合并成一个更大的有序数组。
它将数组平均分成两部分:center=(left+right)/2,当数组分的足够小时(数组中只有一个元素时),只有一个元素的数组自然而然地就可以视为是有序的,此时就可以进行合并操作了。因此,上面讲的合并两个有序的子数组,是从只有一个元素的两个字数组开始合并的。
合并后的元素个数:从1->2->4->8->...
举例:
比如初始数组为:[24,13,25,1,2,27,38,15]
1)分成了两个大小相等的子数组:[24,13,25,1],[2,27,38,15]
2)再划分成四个大小相等的子数组:[24,13],[25,1],[2,27],[38,15]
3)此时,left<right还是成立的,再分为:[24],[13],[25],[1],[2],[27],[38],[15]
此时,有8个小数组,每个数组都可以视为有序的数组!每个数组中的left=right,从递归中返回,故开始执行合并(第21行):
merge([24],[13]),得到[13,24]
merge([25],[1]),得到[1,25]
......
最终得到有序数组。
复杂度分析:
归并排序中,用到了一个临时数组,故空间复杂度为O(n);由归并排序的递归公式:T(n)=2T(n/2)+O(n),可知时间复杂度为O(nlogn)。
归并排序中的比较次数是所有排序中最少的。原因是,它一开始是不断地划分,比较只发生在合并各个有序的子数组时。
稳定性:
归并排序是稳定排序,它也是一种十分高效的排序,能利用完全二叉树特性的排序一般性能都不会太差。Java中Arrays.sort()采用了一种名为TimSort的排序算法,就是归并排序的优化版本。从上图中可以看出,每次合并操作的平均时间复杂度为O(n),而完全二叉树的深度为|O(nlogn)|,总的平均时间复杂度为O(nlogn)。而且,归并排序的最好/最坏平均时间复杂度均为O(nlogn)。
算法实现:
第一种方法:
1 public class MergeSort {
2 /*
3 * 将一个数组中的两个相邻有序区间合并成一个
4 * 参数说明:
5 * a -- 包含两个有序区间的数组
6 * start -- 第1个有序区间的起始地址。
7 * mid -- 第1个有序区间的结束地址。也是第2个有序区间的起始地址。
8 * end -- 第2个有序区间的结束地址。
9 */
10 public static void merge(int[] a, int start, int mid, int end) {
11 int[] tmp = new int[end-start+1]; // tmp是汇总2个有序区的临时区域
12 int i = start; // 第1个有序区的索引
13 int j = mid + 1; // 第2个有序区的索引
14 int k = 0; // 临时区域的索引
15 while(i <= mid && j <= end) {
16 if (a[i] <= a[j])
17 tmp[k++] = a[i++];
18 else
19 tmp[k++] = a[j++];
20 }
21
22 while(i <= mid)
23 tmp[k++] = a[i++];
24
25 while(j <= end)
26 tmp[k++] = a[j++];
27
28 // 将排序后的元素,全部都整合到数组a中。
29 for (i = 0; i < k; i++)
30 a[start + i] = tmp[i];
31
32 tmp=null;
33 }
34
35 /*
36 * 归并排序(从上往下)
37 *
38 * 参数说明:
39 * a -- 待排序的数组
40 * start -- 数组的起始地址
41 * endi -- 数组的结束地址
42 */
43 public static void mergeSortUp2Down(int[] a, int start, int end) {
44 if(a==null || start >= end)
45 return ;
46
47 int mid = (end + start)/2;
48 mergeSortUp2Down(a, start, mid); // 递归排序a[start...mid]
49 mergeSortUp2Down(a, mid+1, end); // 递归排序a[mid+1...end]
50
51 // a[start...mid] 和 a[mid...end]是两个有序空间,
52 // 将它们排序成一个有序空间a[start...end]
53 merge(a, start, mid, end);
54 }
55
56 /*
57 * 对数组a做若干次合并:数组a的总长度为len,将它分为若干个长度为gap的子数组;
58 * 将"每2个相邻的子数组" 进行合并排序。
59 *
60 * 参数说明:
61 * a -- 待排序的数组
62 * len -- 数组的长度
63 * gap -- 子数组的长度
64 */
65 public static void mergeGroups(int[] a, int len, int gap) {
66 int i;
67 int twolen = 2 * gap; // 两个相邻的子数组的长度
68
69 // 将"每2个相邻的子数组" 进行合并排序。
70 for(i = 0; i+2*gap-1 < len; i+=(2*gap))
71 merge(a, i, i+gap-1, i+2*gap-1);
72
73 // 若 i+gap-1 < len-1,则剩余一个子数组没有配对。
74 // 将该子数组合并到已排序的数组中。
75 if ( i+gap-1 < len-1)
76 merge(a, i, i + gap - 1, len - 1);
77 }
78
79 /*
80 * 归并排序(从下往上)
81 *
82 * 参数说明:
83 * a -- 待排序的数组
84 */
85 public static void mergeSortDown2Up(int[] a) {
86 if (a==null)
87 return ;
88
89 for(int n = 1; n < a.length; n*=2)
90 mergeGroups(a, a.length, n);
91 }
92
93 public static void main(String[] args) {
94 int i;
95 int a[] = {80,30,60,40,20,10,50,70};
96
97 System.out.printf("before sort:");
98 for (i=0; i<a.length; i++)
99 System.out.printf("%d ", a[i]);
100 System.out.printf("\n");
101 mergeSortUp2Down(a, 0, a.length-1); // 归并排序(从上往下)
102 //mergeSortDown2Up(a); // 归并排序(从下往上)
103
104 System.out.printf("after sort:");
105 for (i=0; i<a.length; i++)
106 System.out.printf("%d ", a[i]);
107 System.out.printf("\n");
108 }
109 }
第二种方法:
1 public class MergeSortTest {
2 public static void main(String[] args) {
3 int[] data = new int[] { 5, 3, 6, 2, 1, 9, 4, 8, 7 };
4 print(data);
5 mergeSort(data);
6 System.out.println("排序后的数组:");
7 print(data);
8 }
9 public static void mergeSort(int[] data) {
10 sort(data, 0, data.length - 1);
11 }
12 public static void sort(int[] data, int left, int right) {
13 if (left >= right)
14 return;
15 // 找出中间索引
16 int center = (left + right) / 2;
17 // 对左边数组进行递归
18 sort(data, left, center);
19 // 对右边数组进行递归
20 sort(data, center + 1, right);
21 // 合并
22 merge(data, left, center, right);
23 print(data);
24 }
25 /**
26 * 将两个数组进行归并,归并前面 2 个数组已有序,归并后依然有序
27 * @param data
28 * 数组对象
29 * @param left
30 * 左数组的第一个元素的索引
31 * @param center
32 * 左数组的最后一个元素的索引,center+1 是右数组第一个元素的索引
33 * @param right
34 * 右数组最后一个元素的索引
35 */
36 public static void merge(int[] data, int left, int center, int right) {
37 // 临时数组
38 int[] tmpArr = new int[data.length];
39 // 右数组第一个元素索引
40 int mid = center + 1;
41 // third 记录临时数组的索引
42 int third = left;
43 // 缓存左数组第一个元素的索引
44 int tmp = left;
45 while (left <= center && mid <= right) {
46 // 从两个数组中取出最小的放入临时数组
47 if (data[left] <= data[mid]) {
48 tmpArr[third++] = data[left++];
49 } else {
50 tmpArr[third++] = data[mid++];
51 }
52 }
53 // 剩余部分依次放入临时数组(实际上两个 while 只会执行其中一个)
54 while (mid <= right) {
55 tmpArr[third++] = data[mid++];
56 }
57 while (left <= center) {
58 tmpArr[third++] = data[left++];
59 }
60 // 将临时数组中的内容拷贝回原数组中
61 // (原 left-right 范围的内容被复制回原数组)
62 while (tmp <= right) {
63 data[tmp] = tmpArr[tmp++];
64 }
65 }
66 public static void print(int[] data) {
67 for (int i = 0; i < data.length; i++) {
68 System.out.print(data[i] + "\t");
69 }
70 System.out.println();
71 }
72 }
标签:范围 组合 art 技术 缓存 递归算法 ram turn for
原文地址:https://www.cnblogs.com/HuiH/p/11791952.html