标签:complex 微信 循环 两种 斐波那契数列 规模 system ref 运算
什么是算法?算法其实就是对一个问题或一类问题的解决过程的描述。大家对高斯不陌生吧?以首项加末项乘以项数除以2用来计算“1+2+3+4+5+···+(n-1)+n”的结果。我们把它叫做高斯算法,因为可以通过公式来解决复杂的问题,大大缩短了解题时间。当然算法的魅力还不止如此,我们接着往下看:

这两段代码都可以称之为算法,因为分别可以解决两个数相加和从1加到n的问题。算法并不一定要非常复杂,小到一行代码,多到上万行代码,只要能解决特定问题,就是算法。
使用不同算法,解决同一个问题,效率可能相差非常大
现有两个求斐波那契数 (fibonacci number) 的算法
(斐波那契数列:1 1 2 3 5 8 ……)
这里
public static int fib1(int n) {
if (n <= 1) return n;
return fib1(n - 1) + fib1(n - 2);
}public static int fib2(int n) {
if (n <= 1) return n;
int first = 0;
int second = 1;
for (int i = 0; i < n - 1; i++) {
int sum = first + second;
first = second;
second = sum;
}
return second;
}这两个算法哪个更优呢?
如果单从执行效率上进行评估,可能会想到这么一种方案
比较不同算法对同一组输入的执行处理时间
这种方案也叫做:事后统计法
我们的做法是:
public static void main(String[] args) {
int n = 45;//求第45个斐波那契数
TimeTool.check("fib1", new Task() {
public void execute() {
System.out.println(fib1(n));
}
});//5.815秒
TimeTool.check("fib2", new Task() {
public void execute() {
System.out.println(fib2(n));
}
});//0.0秒
}上述方案有比较明显的缺点
执行时间严重依赖硬件以及运行时各种不确定的环境因素
必须编写相应的测算代码
测试数据的选择比较难保证公正性 (n=100时可能第一种算法时间更短,n=200时可能第二种算法时间更短)
一般从以下维度来评估算法的优劣
正确性、可读性、健壮性(对不合理输入的反应能力和处理能力)
时间复杂度(time complexity):估算程序指令的执行次数(执行时间)
空间复杂度(space complexity):估算所需占用的存储空间
我们用这种方案评估一下计算1+2+...+n的算法
显然第二种算法更好。难道是因为第二种方法代码更短吗?斐波那契数列的例子已经告诉我们并不是代码越短越好。这个例子中第二个算法只需要三步运算就可以解决问题,而第一种需要循环n次。首先都满足正确性、可读性、健壮性的条件,然后从时间复杂度来讲,假定一步运算的执行时间的一定的,我们考察一下大致需要执行多少次指令,就可以比较出两种算法的时间长短;再从空间复杂度考虑,需要的变量越少、开辟的存储空间越小,算法更好。
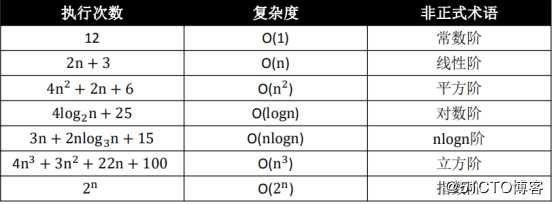
一般用大O表示法来描述复杂度,它表示的是数据规模 n 对应的复杂度
方法步骤:
(1)估算时间复杂度/空间复杂度(主要是时间复杂度)
(2.1)忽略常数、系数、低阶
? $9$>> O(1)
? $2n+6$ >> O(n)
? $n^2+2n+6$ >> O($n^2$)
? $4n^3+3n^2+22n+100$ >> O($n^3$)
(2.2) 对数阶一般省略底数
? $log_2n=log_29+log_9n$ (任意底数的对数可通过乘以一个常数相互转化)
? 所以 $log_2n$、$log_9n$ 统称为 $logn$
注意:大O表示法仅仅是一种粗略的分析模型,是一种估算,能帮助我们短时间内了解一个算法的执行效率
计算下面几段代码的时间复杂度
public static void test1(int n) {
//1(进行一次判断操作)
if (n > 10) {
System.out.println("n > 10");
} else if (n > 5) { // 2
System.out.println("n > 5");
} else {
System.out.println("n <= 5");
}
// 1(定义一次i) + 4(i累加四次) + 4(判断i<4四次) + 4(循环体一条语句执行四次)=9
for (int i = 0; i < 4; i++) {
System.out.println("test");
}
// 大O表示法时间复杂度O(1)
}public static void test2(int n) {
// 1(定义一次i)+ 3n(i累加n次+判断i<n n次+循环体一条语句执行n次)=1+3n
for (int i = 0; i < n; i++) {
System.out.println("test");
}
// 大O表示法时间复杂度O(n)
}public static void test3(int n) {
// 1(定义一次i) + 2n(i累加n次+判断i<n n次) + n(外层循环体语句执行n次) * (1(定义一次j) + 3n(j累加n次+判断j<n n次+内层循环体一条语句执行n次))=3n^2 + 3n + 1
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
System.out.println("test");
}
}
// 大O表示法时间复杂度O(n^2)
}
public static void test4(int n) {
// 8 = 2^3
// 16 = 2^4
// 3 = log2(8)
// 4 = log2(16)
// 执行次数 = log2(n)
while ((n = n / 2) > 0) {
System.out.println("test");
}
// 大O表示法时间复杂度O(logn)
}public static void test5(int n) {
// log5(n)
while ((n = n / 5) > 0) {
System.out.println("test");
}
// 大O表示法时间复杂度O(logn)
}public static void test7(int n) {
// 1(定义一次i) + 2*log2(n)(i*2运算次数) + log2(n)(外层循环执行次数) * (1 + 3n)(内层循环执行次数)
for (int i = 1; i < n; i = i * 2) {
// 1 + 3n
for (int j = 0; j < n; j++) {
System.out.println("test");
}
}
// 1 + 3*log2(n) + 2 * nlog2(n)
// 大O表示法时间复杂度O(nlogn)
}
$O(1)<O(logn)<O(n)<O(nlogn)<O(n^2)<O(n^3)<O(2n)<O(n!)<O(n^n)$
可以借助函数生成工具对比复杂度的大小
https://zh.numberempire.com/graphingcalculator.php
总而言之,现今大数据时代,算法的使用和研发越来越受人瞩目。算法也逐渐进入人们的生活。篇幅有限,在此不再过多讲解算法的知识。我们下期再会。
如果您想提升自己,学习更多算法、高级编程语言技巧,这里有免费的相关学习资料,欢迎加微信:19950277730获取更多技术提升秘籍。这里不仅有志同道合的小伙伴,更有无数免费编程技巧、学习视频和资料,加上微信来一起探讨学习技术吧!!
标签:complex 微信 循环 两种 斐波那契数列 规模 system ref 运算
原文地址:https://blog.51cto.com/14606540/2449259