标签:jin python 广州 htm data 接下来 pre 重庆 imp
https://www.cnblogs.com/jin-liang/p/9064020.html
数据的导入
> data=read.csv(‘F:/R语言工作空间/pca/data.csv‘) #数据的导入 > > ls(data) #ls()函数列出所有变量 [1] "X" "不良贷款率" "存贷款比率" "存款增长率" "贷款增长率" "流动比率" "收入利润率" [8] "资本充足率" "资本利润率" "资产利润率" > dim(data) # 维度 [1] 15 10
> std_data=scale(data[2:10]) #数据标准化 > > rownames(std_data)=data[[1]] #数组各行名字定义为数据文件的的第一列 > > class(std_data) #查看数据类型 [1] "matrix" > df=as.data.frame(std_data) #转化为数据框 > class(df) [1] "data.frame"
习惯数据框格式
数据标准化
> std_data=scale(data[2:10]) #数据标准化 > > rownames(std_data)=data[[1]] #数组各行名字定义为数据文件的的第一列 > > class(std_data) #查看数据类型 [1] "matrix" > df=as.data.frame(std_data) #转化为数据框 > class(df) [1] "data.frame"
> df.pr=princomp(df,cor=TRUE) #主成分分析
> summary(df.pr,loadings=TRUE) #列出结果 包含特征向量<br>
Importance of components:
Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7 Comp.8 Comp.9
Standard deviation 1.8895 1.3087 1.2365 0.9593 0.86553 0.46727 0.4168 0.293547 0.201641
Proportion of Variance 0.3967 0.1903 0.1699 0.1023 0.08324 0.02426 0.0193 0.009574 0.004518
Cumulative Proportion 0.3967 0.5870 0.7569 0.8591 0.94235 0.96661 0.9859 0.995482 1.000000
Loadings:
Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7 Comp.8 Comp.9
不良贷款率 0.425 0.188 0.288 0.423 0.173 0.695
资本充足率 -0.359 -0.521 0.234 0.546 0.127 -0.214 -0.426
存贷款比率 0.301 0.532 -0.142 -0.370 -0.324 0.248 -0.320 -0.438
流动比率 -0.192 0.429 -0.416 0.439 0.306 -0.384 -0.113 0.399
资产利润率 -0.392 0.332 -0.438 -0.178 0.452 0.494 0.238
资本利润率 -0.413 -0.185 0.259 -0.103 0.428 -0.562 0.167 -0.436
收入利润率 -0.299 -0.455 -0.116 0.299 -0.481 -0.159 0.432 -0.329 0.221
存款增长率 -0.243 0.249 0.387 0.636 -0.282 0.171 0.336 -0.309
贷款增长率 -0.300 0.342 0.518 -0.127 0.101 0.214 -0.620 0.260
结果比较杂乱,接下来确定主成分个数
根据累计贡献率大于90%,确定
计算相关系数矩阵
> cor(df) #相关系数矩阵
不良贷款率 资本充足率 存贷款比率 流动比率 资产利润率 资本利润率 收入利润率 存款增长率
不良贷款率 1.0000 -0.57238 0.31761 -0.20055 -0.70121 -0.45662 -0.53825 -0.16790
资本充足率 -0.5724 1.00000 -0.33566 0.61749 0.51053 0.32931 0.37424 0.01208
存贷款比率 0.3176 -0.33566 1.00000 0.16576 -0.02387 -0.72464 -0.56974 -0.11599
流动比率 -0.2005 0.61749 0.16576 1.00000 0.31280 0.07588 -0.03629 0.27787
资产利润率 -0.7012 0.51053 -0.02387 0.31280 1.00000 0.44019 0.13002 0.24387
资本利润率 -0.4566 0.32931 -0.72464 0.07588 0.44019 1.00000 0.38484 0.26496
收入利润率 -0.5383 0.37424 -0.56974 -0.03629 0.13002 0.38484 1.00000 0.24963
存款增长率 -0.1679 0.01208 -0.11599 0.27787 0.24387 0.26496 0.24963 1.00000
贷款增长率 -0.2863 0.03398 -0.14413 0.08791 0.59245 0.55095 -0.09947 0.60455
贷款增长率
不良贷款率 -0.28628
资本充足率 0.03398
存贷款比率 -0.14413
流动比率 0.08791
资产利润率 0.59245
资本利润率 0.55095
收入利润率 -0.09947
存款增长率 0.60455
贷款增长率 1.00000
求特征值和特征向量
>y=eigen(cor(df)) #求出cor(df)的特征值和特征向量 > y$values#输出特征值 [1] 3.57008 1.71263 1.52895 0.92033 0.74914 0.21834 0.17370 0.08617 0.04066
输出前五个累计贡献率
> sum(y$values[1:5])/sum(y$values) #求前5个主成分的累计方差贡献率 [1] 0.9423
输出前5个主成分的载荷矩阵
> df.pr$loadings[,1:5]#输出前5个主成分的载荷矩阵
Comp.1 Comp.2 Comp.3 Comp.4 Comp.5
不良贷款率 0.4245 0.03196 0.18753 0.28824 0.4226
资本充足率 -0.3595 0.02955 -0.52091 0.04673 0.2341
存贷款比率 0.3013 0.53170 -0.14155 -0.09645 -0.3697
流动比率 -0.1923 0.42903 -0.41595 0.43880 0.3061
资产利润率 -0.3916 0.33239 -0.04543 -0.43786 -0.1780
资本利润率 -0.4134 -0.18527 0.25918 -0.10322 0.4280
收入利润率 -0.2990 -0.45539 -0.11566 0.29949 -0.4810
存款增长率 -0.2432 0.24926 0.38706 0.63621 -0.2824
贷款增长率 -0.3000 0.34207 0.51768 -0.12671 0.1011
画出碎石图
screeplot(df.pr,type=‘lines‘) #画出碎石图
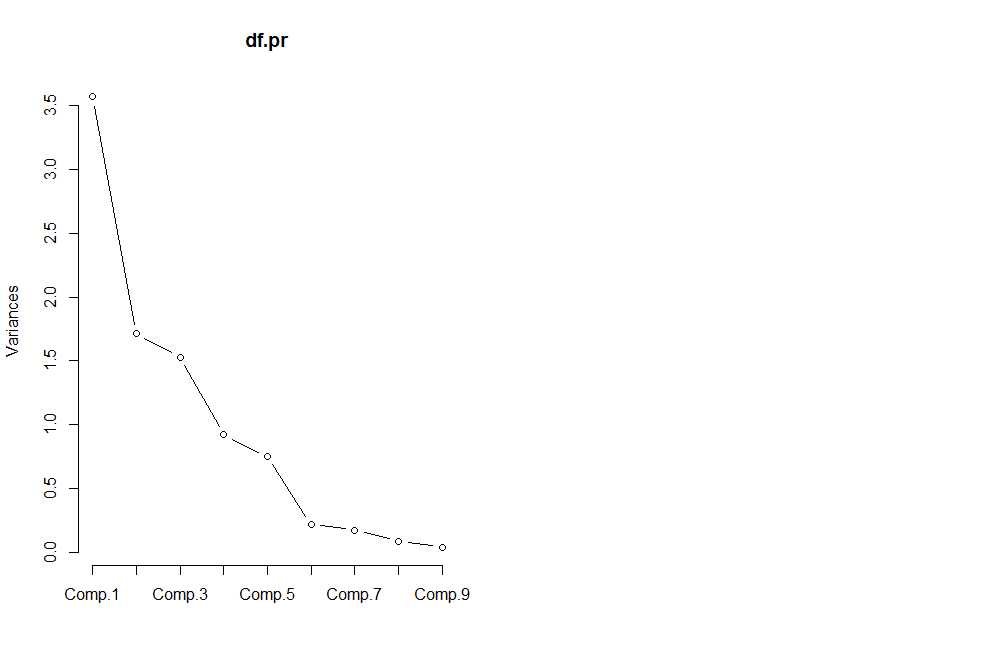
画出散点图
biplot(df.pr) #画出主成分散点图
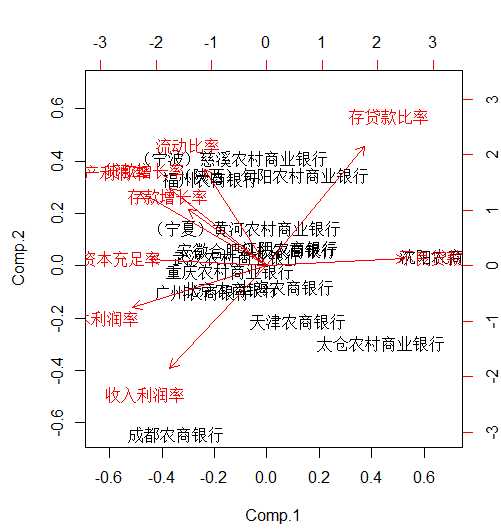
> y=eigen(cor(df)) #求出cor(df)的特征值和特征向量 > y$values#输出特征值 [1] 3.57008 1.71263 1.52895 0.92033 0.74914 0.21834 0.17370 0.08617 0.04066
> s=df.pr$scores[,1:5]#输出前5个主成分的得分
> #s[,1]
> #计算综合得分
>
> scores=0.0
> for (i in 1:5)
scores=(y$values[i]*s[,i])/(sum(y$values[1:5]))+scores
>
>
> cbind(s,scores)#输出综合得分信息
Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 scores
北京农商银行 -0.9927 -0.4565 -0.773341 0.72371 0.5357 -0.52362
上海农商银行 0.5461 -0.4069 0.228600 -0.05691 -1.1411 0.08196
广州农商银行 -1.7680 -0.5058 0.091704 0.46582 0.4301 -0.74130
天津农商银行 0.8670 -1.0680 -0.118665 -1.13960 -0.2242 -0.01556
(宁波)慈溪农村商业银行 -0.9713 2.0909 -2.590721 0.44416 0.7692 -0.33751
江阴农商银行 0.6533 0.3486 -1.678249 0.47363 -0.4051 0.05848
成都农商银行 -2.5372 -3.2477 0.008494 0.24227 1.2955 -1.58158
重庆农村商业银行 -1.0099 -0.1061 1.753280 0.23145 -0.6871 -0.16602
(宁夏)黄河农村商业银行 -0.5903 0.7269 1.227349 0.59878 -1.1312 0.08463
(陕西)旬阳农村商业银行 0.1928 1.7666 -0.273642 -1.29087 0.7258 0.31262
太仓农村商业银行 3.1937 -1.4905 -1.089861 -1.17931 -0.6266 0.66358
武汉农村商业银行 -0.8349 0.1686 -0.119553 -1.63283 -0.4856 -0.55902
安徽合肥科技农商银行 -0.2713 0.3084 -0.273867 1.79049 -1.2170 -0.01448
福州农商银行 -1.5557 1.6844 2.185117 -0.80662 0.7243 0.05566
沈阳农商银行 5.0781 0.1871 1.423354 1.13584 1.4374 2.68217
标签:jin python 广州 htm data 接下来 pre 重庆 imp
原文地址:https://www.cnblogs.com/jiaxinwei/p/11832358.html