日日算法：Kruskal算法

标签：理解   arch   argument   null   假设   生成   out   ring   tps   

介绍

克鲁斯卡尔（Kruskal）算法是用来求出连通图中最小生成树的算法。

连通图：指==无向图==中==任意两点都能相通==的图。
最小生成树：指联通图的所有生成树中==边权重的总和最小==的树（即，找出一个树，让其联通所有的点，并让树的边权和为最小）。

算法思想

克鲁斯卡尔算法的主要基本思想有两点原则：

• 按照从小到大的顺序选择边，并将边的两端连线，构成新的图
• 保证新加入的边不能在新的图上形成环
• 重复以上步骤，直至添加n-1条边
  用图表示该算法的解体过程：
  

算法证明

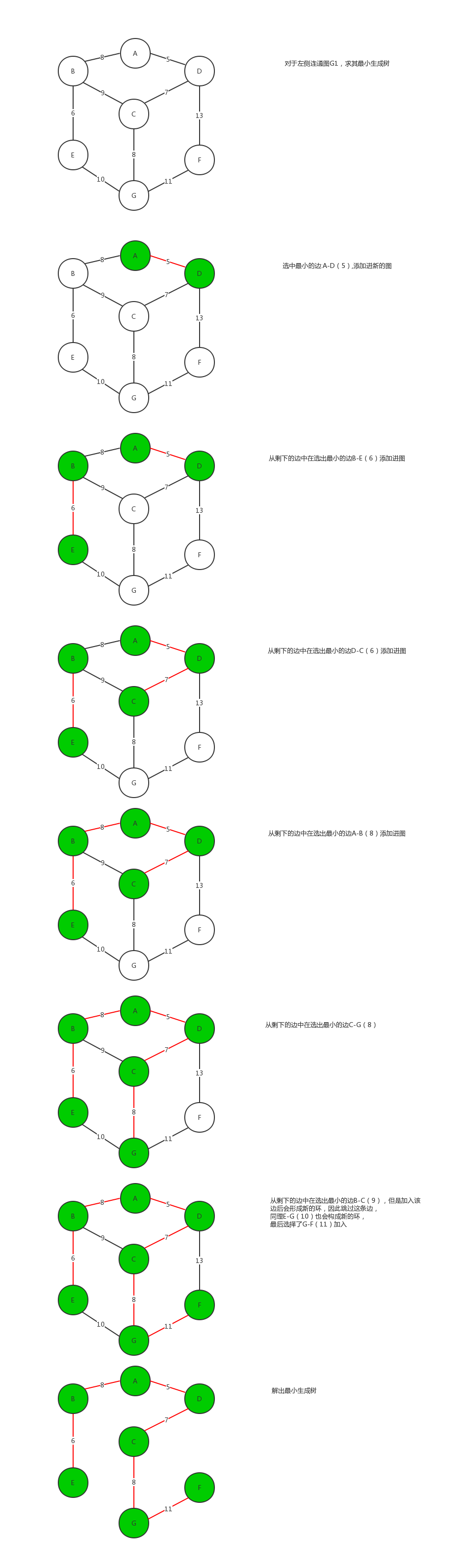
我是通过反证的方式理解该算法的。

1. 证明按上述算法添加n-1条边时，一定能连通n个节点。

   证明：Kruskal算法保证了针对n个节点，它添加了n-1条边，且不存在环。那么假设这n-1条边没有全部连通n个节点。也就说至少有1个点没有边，那么至多只有n-1个点使用n-1条边，当n-1个点使用n-1条边时，必定构成环。与要求不符，故反正成立。

2. 证明新的图中再添加一条边，一定构成环。

   步骤一证明了新生成的图一定是一个连通图，也就是任意两点之间必定已经相连，当我们在加入一条新的边的时候，边两段的点又多了一条新相连的路，因此构成了环。

3. 证明在构成新的环中，新加入的边一定是最长的边。

   假设新加入的边，并非是环中最大的边，那么可以去掉这个环中最大的边，且剩下的边不够环，这与逐步加入小的边且不构成环这一条件矛盾。因此证明新加入的边一定为最长的边。

算法实现

public class Kruskal {

    public static void generateMinTree(int[][] graph){
        if(graph == null || graph.length <=0)
            throw new IllegalArgumentException();

        int minSum = 0;
        //标记哪些点已经到访过
        int[][] visited = new int[graph.length][graph.length];

        //用来表示父子级的关系，验证是否存在环
        int[] nodeHierarchy = new int[graph.length];
        for(int i=0; i<nodeHierarchy.length; i++){
            nodeHierarchy[i] = i;
        }

        int n = 0;
        while(n < graph.length -1){
            int minVal = Integer.MAX_VALUE;
            int iIndex = 0;
            int jIndex = 0;

            for(int i=0; i<graph.length; i++){
                for(int j=i+1; j<graph[i].length; j++){
                    if(graph[i][j] != Integer.MAX_VALUE && visited[i][j] == 0 && graph[i][j] < minVal){
                        iIndex = i;
                        jIndex = j;
                        minVal = graph[i][j];
                    }
                }
            }
            visited[iIndex][jIndex] = 1;

            //判断父节点是否相同，确定是否构成了环
            if(findFather(nodeHierarchy, iIndex) != findFather(nodeHierarchy, jIndex)){
                System.out.println(n + " Round min value path: " + minVal + " from " + iIndex + " to " + jIndex);
                minSum += graph[iIndex][jIndex];
                updateHierarchy(nodeHierarchy, iIndex, jIndex);
                n++;
            }
            System.out.println("node hierarchy:" + Arrays.toString(nodeHierarchy));


        }

        System.out.println("min tree path sum:" + minSum);
        System.out.println("node hierarchy:" + Arrays.toString(nodeHierarchy));


    }

    //递归查找父节点
    private static int findFather(int[] nodeHierarchy, int idx){

        if(nodeHierarchy[idx] == idx)
            return idx;

        return findFather(nodeHierarchy, nodeHierarchy[idx]);

    }

    //递归更新父节点
    private static void updateHierarchy(int[] nodeHierarchy, int from, int to){
        if(nodeHierarchy[from] != from)
            updateHierarchy(nodeHierarchy, nodeHierarchy[from], from);
        nodeHierarchy[from] = to;
    }

}

上述代码见Github。

日日算法：Kruskal算法

标签：理解   arch   argument   null   假设   生成   out   ring   tps   

原文地址：https://www.cnblogs.com/insaneXs/p/11844443.html