标签：word   聚类   关系   模型   stand   偏差   身高   art   AMM   

K-近邻算法

K-K个

N-nearest-最近

N-Neighbor

来源：KNN算法最早是由Cover和Hart提出的一种分类算法

定义

如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别，则该样本也属于这个类别。

距离公式

两个样本的距离可以通过如下公式计算，又叫欧式距离

KNN算法流程总结

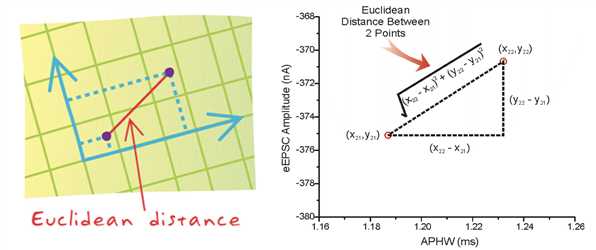
根据K个邻居判定你的类别

1.计算当前样本与所有样本距离

2.距离从小到大排序

3.取前K个邻居

4.K个邻居投票，统计投票结果（A,B）

5.根据投票结果值出现频率高类别作为最终类别

K近邻算法api初步使用

机器学习流程

1.获取数据

2.数据基本处理

3.特征工程

4.建立模型

　　1.KNN算法

5.模型评估

Scikit-learn工具介绍

Python语言的机器学习工具

Scikit-learn包括许多知名的机器学习算法的实现

Scikit-learn文档完善，容易上手，丰富的API

目前稳定版本0.19.1-？？

安装：

pip3 install scikit-learn==0.19.1
注：安装scikit-learn需要Numpy, Scipy等库

Scikit-learn 包含的内容

分类、聚类、回归

特征工程

模型选择、调优

K-近邻算法API

• sklearn.neighbors.KNeighborsClassifier(n_neighbors=5)
  • n_neighbors：int,可选（默认= 5），k_neighbors查询默认使用的邻居数

案例

1. 实例化
2. 执行训练
3. 预测

步骤分析

• 1.获取数据集
• 2.数据基本处理（该案例中省略）
• 3.特征工程（该案例中省略）
• 4.机器学习
• 5.模型评估（该案例中省略）

代码过程

• 导入模块

from sklearn.neighbors import KNeighborsClassifier

• 构造数据集

x = [[0], [1], [2], [3]]
y = [0, 0, 1, 1]

• 机器学习 -- 模型训练

# 实例化API
estimator = KNeighborsClassifier(n_neighbors=2)
# 使用fit方法进行训练
estimator.fit(x, y)

estimator.predict([[1]])

Scikit-learn小结

• sklearn的优势:
  • 文档多,且规范
  • 包含的算法多
  • 实现起来容易
• knn中的api
  • sklearn.neighbors.KNeighborsClassifier(n_neighbors=5)

距离度量

欧氏距离

曼哈顿距离

　　每个维度的差值的绝对值的和

切比雪夫距离

　　每个维度差值绝对值的最大值

闵可夫斯基距离

闵氏距离不是一种距离，而是一组距离的定义，是对多个距离度量公式的概括性的表述。

两个n维变量a(x11,x12,…,x1n)与b(x21,x22,…,x2n)间的闵可夫斯基距离定义为：

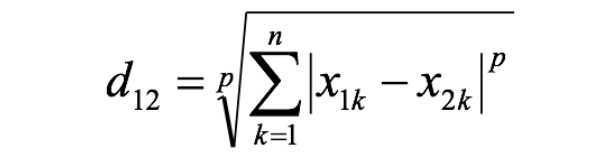
其中p是一个变参数：

当p=1时，就是曼哈顿距离；

当p=2时，就是欧氏距离；

当p→∞时，就是切比雪夫距离。

根据p的不同，闵氏距离可以表示某一类/种的距离。

小结：

1 闵氏距离，包括曼哈顿距离、欧氏距离和切比雪夫距离都存在明显的缺点:

e.g. 二维样本(身高[单位:cm],体重[单位:kg]),现有三个样本：a(180,50)，b(190,50)，c(180,60)。

a与b的闵氏距离（无论是曼哈顿距离、欧氏距离或切比雪夫距离）等于a与c的闵氏距离。但实际上身高的10cm并不能和体重的10kg划等号。

2 闵氏距离的缺点：

? (1)将各个分量的量纲(scale)，也就是“单位”相同的看待了;

? (2)未考虑各个分量的分布（期望，方差等）可能是不同的。

标准化欧氏距离

余弦距离

cos [-1,1] 邻边比斜边

两个量方向差距，趋向1关系比较大

汉明距离

杰卡德距离

杰卡德系数

马氏距离

 小结

• 1.欧式距离(Euclidean Distance)【知道】：
  • 通过距离平方值进行计算
• 2.曼哈顿距离(Manhattan Distance)【知道】：
  • 通过距离的绝对值进行计算
• 3.切比雪夫距离 (Chebyshev Distance)【知道】：
  • 维度的最大值进行计算
• 4.闵可夫斯基距离(Minkowski Distance)【知道】：
  • 当p=1时，就是曼哈顿距离；
  • 当p=2时，就是欧氏距离；
  • 当p→∞时，就是切比雪夫距离。
• 前四个距离公式小结:前面四个距离公式都是把单位相同看待了,所以计算过程不是很科学
• 5.标准化欧氏距离 (Standardized EuclideanDistance)【知道】：
  • 在计算过程中添加了标准差,对量刚数据进行处理
• 6.余弦距离(Cosine Distance)【知道】：
  • 通过cos思想完成
• 7.汉明距离(Hamming Distance)【了解】：
  • 一个字符串到另一个字符串需要变换几个字母,进行统计
• 8.杰卡德距离(Jaccard Distance)【了解】：
  • 通过交并集进行统计
• 9.马氏距离(Mahalanobis Distance)【了解】
  • 通过样本分布进行计算

K值的选择（KNN中）

K值选择问题，李航博士的一书「统计学习方法」上所说：

1) 选择较小的K值，就相当于用较小的领域中的训练实例进行预测，“学习”近似误差会减小，只有与输入实例较近或相似的训练实例才会对预测结果起作用，与此同时带来的问题是“学习”的估计误差会增大，换句话说，K值的减小就意味着整体模型变得复杂，容易发生过拟合；

2) 选择较大的K值，就相当于用较大领域中的训练实例进行预测，其优点是可以减少学习的估计误差，但缺点是学习的近似误差会增大。这时候，与输入实例较远（不相似的）训练实例也会对预测器作用，使预测发生错误，且K值的增大就意味着整体的模型变得简单。

3) K=N（N为训练样本个数），则完全不足取，因为此时无论输入实例是什么，都只是简单的预测它属于在训练实例中最多的类，模型过于简单，忽略了训练实例中大量有用信息。

在实际应用中，K值一般取一个比较小的数值，例如采用交叉验证法（简单来说，就是把训练数据在分成两组:训练集和验证集）来选择最优的K值。

• 近似误差：
  • 对现有训练集的训练误差，关注训练集，
  • 如果近似误差过小可能会出现过拟合的现象，对现有的训练集能有很好的预测，但是对未知的测试样本将会出现较大偏差的预测。
  • 模型本身不是最接近最佳模型。
• 估计误差：
  • 可以理解为对测试集的测试误差，关注测试集，
  • 估计误差小说明对未知数据的预测能力好，
  • 模型本身最接近最佳模型。

总结：

• K值过小：

　　　　容易受到异常点的影响

　　　　容易过拟合

• K值过大：

　　　　受到样本均衡问题的影响

　　　　容易欠拟合

K-近邻算法（KNN）

标签：word   聚类   关系   模型   stand   偏差   身高   art   AMM   

原文地址：https://www.cnblogs.com/mujun95/p/11847730.html