标签:并且 归并 return 分而治之 版本 int amp 归并排序 code
一、什么是归并排序?
归并排序是基于分而治之的思想建立起来的。
所谓的分而治之,也就是将一个数据规模为N的数据集,分解为两个规模大小差不多的数据集(n/2),然而分别处理这两个更小的问题,就相当于解决了总的问题。
二、归并排序的思路。
1-首先将数据分为左右相等的两部分,不断细分,到最后只有单个元素。
2-再将相邻的两个元素集合(只是规模为1)排序,变为 n/2 个规模为2的数据序列。
随后不断的合并数据集并且排序,直到最后得到了一个完整的数据有序序列。
三、一个简单的例子。
下图是一个数据规模为8的数据集的排序过程。
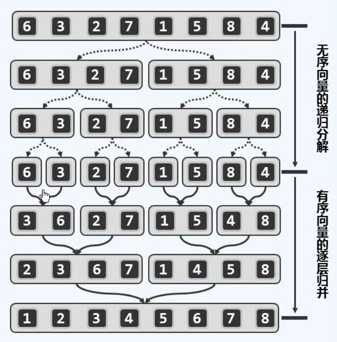
最开始8个数据不断地细分,知道不可再分(数据数目为一)
随后开始进行排序,将相邻的两个数据集排序合并,形成3 6,2 7, 1 5 ,4, 8
随后不断地向上排序,知道合并成一个完整的有序数据序列。
四 算法功能
上面的过程说明了算法需要完成的两个的算法功能
一是对于数据二分的过程,直到不可再分
二是对于两个数据集排序合并,形成一个更大的数据集的过程。
五、算法实现
1-递归版本

1 #include <stdlib.h> 2 #include <stdio.h> 3 4 void Merge(int sourceArr[],int tempArr[], int startIndex, int midIndex, int endIndex) 5 { 6 int i = startIndex, j=midIndex+1, k = startIndex; 7 while(i!=midIndex+1 && j!=endIndex+1) 8 { 9 if(sourceArr[i] > sourceArr[j]) 10 tempArr[k++] = sourceArr[j++]; 11 else 12 tempArr[k++] = sourceArr[i++]; 13 } 14 while(i != midIndex+1) 15 tempArr[k++] = sourceArr[i++]; 16 while(j != endIndex+1) 17 tempArr[k++] = sourceArr[j++]; 18 for(i=startIndex; i<=endIndex; i++)//这里的复制是从头到尾的, 19 //我之前就是这里出了问题 20 sourceArr[i] = tempArr[i]; 21 } 22 23 //内部使用递归 24 void MergeSort(int sourceArr[], int tempArr[], int startIndex, int endIndex) 25 { 26 int midIndex; 27 if(startIndex < endIndex) 28 { 29 midIndex = startIndex + (endIndex-startIndex) / 2;//避免溢出int 30 MergeSort(sourceArr, tempArr, startIndex, midIndex); 31 MergeSort(sourceArr, tempArr, midIndex+1, endIndex); 32 Merge(sourceArr, tempArr, startIndex, midIndex, endIndex); 33 } 34 } 35 36 int main(int argc, char * argv[]) 37 { 38 int a[8] = {50, 10, 20, 30, 70, 40, 80, 60}; 39 int i, b[8]; 40 MergeSort(a, b, 0, 7); 41 for(i=0; i<8; i++) 42 printf("%d ", a[i]); 43 printf("\n"); 44 return 0; 45 }
2-迭代版本
(待补充)
六、复杂度
时间复杂度: O(n log n)
空间复杂度:O(n)
标签:并且 归并 return 分而治之 版本 int amp 归并排序 code
原文地址:https://www.cnblogs.com/fantianliang/p/11874813.html